Prostorová napjatost

Definice napjatosti

Napjatost popisuje stav vnitřního namáhání materiálu způsobeného vnějšími zatíženími. Je charakterizována napětím, což je síla připadající na jednotkovou plochu. Vektor napětí na určité ploše v těle závisí na orientaci této plochy a bodě v tělese.

Principy prostorové napjatosti

Uvažujme prut se čtvercovým průřezem, který je vystaven tahové síle F. Tato síla v prutu způsobé napětí

\[ T = \sigma = \frac{\text{síla}}{\text{plocha}} = \frac{F}{A_0} \quad [\text{N}/\text{mm}^2] \]

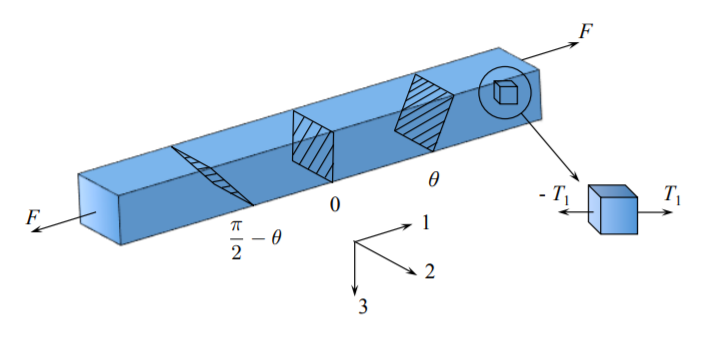
kde \(\vec{T}\) definujeme také jako vektor napětí neboli trakční vektor

\[ \vec{T} = \frac{\vec{F}}{A_0} \]

V jednoosém případě je povrchové napětí jedinou složkou tenzoru napětí v globálním souřadném systému, běžně označovanou jako \(\sigma\).

Note

Jak aplikovat sílu na konec prutu?

To lze provést několika různými způsoby (viz obrázek níže). Ke konci prutu může být přilepena (nebo přivařena) spojka s čepem, nebo může být skrz prut provrtán otvor pro uchycení čepem.

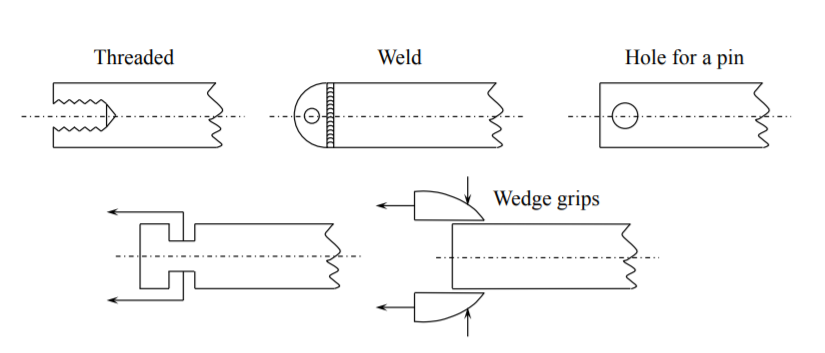
Alternativně může být vyroben vnitřní či vnější závit. Nakonec může být axiální síla aplikována pomocí třecích nebo mechanických čelistí.

Kromě případů s přivařenou nebo přilepenou spojkou vzniká v oblasti konců prutu složitý stav napjatosti, který je vícesložkový (multiaxiální). Takový stav napětí je omezen na poměrně krátký úsek prutu, srovnatelný s jeho výškou nebo průměrem. V tomto úseku dochází k postupnému přechodu z vícesložkového stavu napjatosti do jednoosého stavu, pro který platí rovnice (2.1.1).

Výše uvedený příklad může sloužit jako praktická aplikace Saint-Venantova principu (1856). Tento princip, pojmenovaný po francouzském teoretikovi pružnosti Jeanu Claudu Barrém de Saint-Venant, lze formulovat následovně:

„Rozdíl mezi účinky dvou různých, ale staticky ekvivalentních zatížení se stává velmi malým ve dostatečně velké vzdálenosti od místa zatížení.“

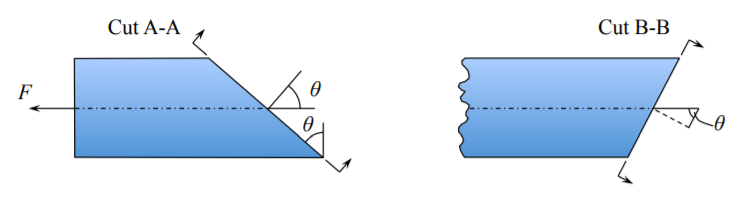
Zamysleme se – jaká jsou „dvě“ staticky ekvivalentní zatížení aplikovaná na konce prutu? Obvykle uvažujeme průřez kolmý na osu prutu. Nyní však zvažme dva řezy pod úhly \(\theta\) a \(\pi/2-\theta\) vůči normálnímu směru. Tyto roviny jsou definovány jednotkovým normálovým vektorem \(\vec{n}\).

Z uvolnění tělesa dostáváme složky normálové a tečné síly:

\[ F_N = F \cos\theta \]

\[ F_n = F \cos\left(\frac{\pi}{2} - \theta\right) \]

\[ F_T = F \sin\theta \]

\[ F_t = F \sin\left(\frac{\pi}{2} - \theta\right) \]

Šikmý průřez A je větší a souvisí s referenčním průřezem následovně:

\[ A_0 = A_A \cos\theta,\quad A_0 = A_B \cos\left(\frac{\pi}{2} - \theta\right) \]

Zvažme nyní jednotkový objemový krychlový prvek umístěný v průsečíku řezů A-A a B-B.

Objemový prvek s povrchovým napětím působícím na dvou sousedních stěnách.

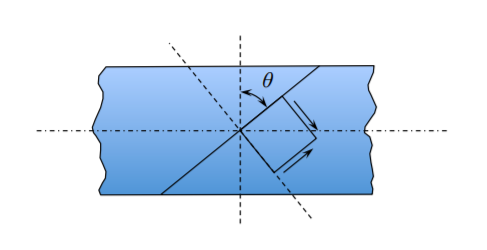
Povrchové napětí (síla na jednotku plochy) na dvou kolmých rovinách jsou:

• Rovina rovnoběžná s A-A: $\( T_N = T \cos^2 \theta \)\( \)\( T_T = T \sin \theta \cos \theta \)$

• Rovina rovnoběžná s B-B: $\( T_n = T \cos^2 \left(\frac{\pi}{2}) - \theta \right) \)\( \)\( T_t = T \sin \left(\frac{\pi}{2}) - \theta \right) \cos \left(\frac{\pi}{2}) - \theta \right) \)$

Lze si všimnout, že tečné složky vektoru povrchové trakce na řezech A-A a B-B jsou totožné. Normalizované grafy výše uvedených veličin v závislosti na úhlu orientace řezu jsou znázorněny na obrázku.

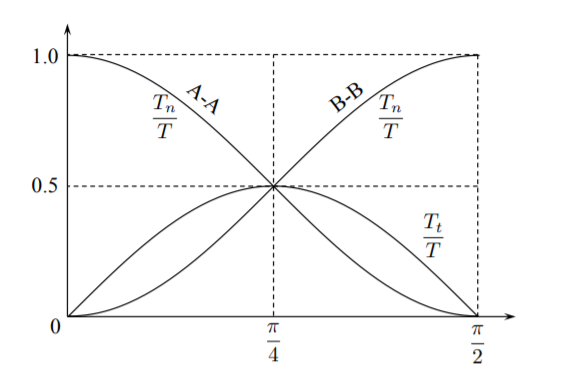
Lze si všimnout, že tangenciální složka dosahuje maxima při úhlu 45°. To znamená, že pokud materiál selže v důsledku smykového zatížení, bude lomová plocha vždy orientována pod úhlem 45°. Výše uvedený příklad nás učí, že existuje nekonečně mnoho kombinací normálové a tečné složky povrchových tahů, které jsou v rovnováze s působícím zatížením. Pro každou orientaci průřezu existuje jiná dvojice \(\{T_n, T_t\}\).

Orientace povrchového prvku je jednoznačně určena jednotkovým normálovým vektorem \(\mathbf{n} = [n_1, n_2, n_3]\). Současně jsou složky povrchového vektoru napětí (trakčního vektoru) působícího na tentýž prvek \(\mathbf{T} = [T_1, T_2, T_3]\).

Cauchyho tenzor napětí

Stav napjatosti materiálu je tedy definován množinou všech vektorů napětí \(\vec{T}^n\) spojených s někonečným počtem rovin protínající daný body. Ve dvou rozměrech byla řešením problému Mohrova kružince, kde ze znalosti dvou rovin bylo možné dopočítat napětí v libovolné jiné rovině. Ve třech rozměrech je logické předpokládat, že budeme potřebovat tři roviny. Z důvodu jedoduchosti uvažujme stav, kdy jednotlivé roviny jsou navzájem kolmé a tvoří tak elementární hranol. Napětí v libovolné jiné rovině tak můžeme získat prostřednictvím transformace souřadnic.

Pro sjednodušení, uvažujeme-li na čtyřstěn, kde tři z jeho stran jsou definovány rovinami souřadnicového systému a čtvrtá strana je defonována jednotkovým vektorem \(\vec{n}\) a velikostí \(\mathrm{d}A\)

Vektor napětí v dané rovinš je definován jako \(\vec{T}_n\). Podobně můžeme definovat vektory zbylých rovin jako \(\vec{T}_i\), \(\vec{T}_j\) a \(\vec{T}_k\), kde \(\vec{i}, \vec{j}, \vec{k}\) jsou jednotkové vektory (verzory) ve směru \(x, y\) a \(z\). Tento čtyřstěn je někdy označován jako Cauchyho čtyřstěn. Když budeme předpokládat, že objem čtyřstěnu je malý, můžeme zanedbat jeho tíhu a pro rovnováhu sil plyne

\[ \vec{T}_n dA - \vec{T}_i dA_x - \vec{T}_j dA_y - \vec{T}_k dA_z = 0 \]

Kde záporné znaménka značí, žě normála je ve směru záporného směru dané osi. PRop jednotlivé plochy platí, že velikost plochy je dána průmětem do plochy \(\mathrm{d}A\) do dané roviny.

\[ \mathrm{d}A_x = (\vec{n} \cdot \vec{i}) \mathrm{d}A = n_x \mathrm{d}A \]

\[ \mathrm{d}A_y = (\vec{n} \cdot \vec{j}) \mathrm{d}A = n_y \mathrm{d}A \]

\[ \mathrm{d}A_z = (\vec{n} \cdot \vec{k}) \mathrm{d}A = n_z \mathrm{d}A \]

Rovnováhu sil tak můžeme sjednodušit do tvaru

\[ \vec{T}_n = \vec{T}_i n_x + \vec{T}_j n_y - \vec{T}_k n_z = 0 \]

kde jednotlivé vektory napětí (trakční vektory) můžeme vyjádřit pomocí jejich složek

\[\vec{T}_x = T_{xx} \vec{i} + T_{xy} \vec{j} + T_{xz} \vec{k} = \sigma_{xx} \vec{i} + \sigma_{xy} \vec{j} + \sigma_{xz} \vec{k}\]

\[\vec{T}_y = T_{yx} \vec{i} + T_{yy} \vec{j} + T_{yz} \vec{k} = \sigma_{yx} \vec{i} + \sigma_{yy} \vec{j} + \sigma_{yz} \vec{k}\]

\[\vec{T}_z = T_{zx} \vec{i} + T_{zy} \vec{j} + T_{zz} \vec{k} = \sigma_{zx} \vec{i} + \sigma_{zy} \vec{j} + \sigma_{zz} \vec{k}\]

Děvet složek vektorů napětí je možné zapsat ve tvaru tenzoru druhého řádu

\[\begin{split} \boldsymbol{\sigma} = \sigma_{ij} = \begin{bmatrix} \vec{T}_x \\ \vec{T}_y \\ \vec{T}_z \end{bmatrix} = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \tau_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix} = \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{bmatrix} \end{split}\]

Vektor napětí v lobvolné rovině můžeme určit

\[ \vec{T}_n = \vec{T}_i n_x + \vec{T}_j n_y - \vec{T}_k n_z = \sum\limits_i \left(\sum\limits_j \sigma_{ij} \vec{e}_j\right) n_i = \sum\limits_j \left(\sum\limits_i \sigma_{ij} {n}_i\right) \vec{e}_j = \sum_j T^n_j \vec{e}_j \]

Případně to můžeme napsat ve maticovém zápisu

\[\begin{split} \left[T_x, T_y, T_z\right] = \left[ n_x, n_y, n_z \right] \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \tau_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix} \end{split}\]

nebo jednoduše

\[\vec{T_n} = \vec{n} \cdot \boldsymbol{\sigma}\]

Složky vektoru napětí (trakčního vektoru) v dané rovině

Složky povrchového trakčního vektoru působícího na rovinu jsou \(\mathbf{T} = [T_1, T_2, T_3]\). Například orientace rovin jednotkové hmotné krychle je znázorněna na obrázku.

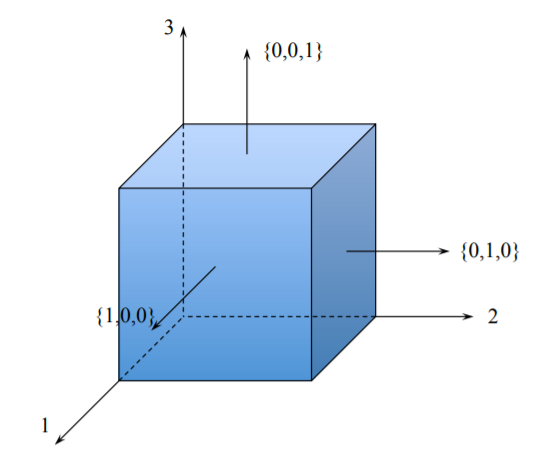Vztah mezi vektory napětí v daných rovinách, jednotkovým normálovým vektorem definujícím rovinu a tenzorem napětí je dán slavným Cauchyho vzorcem:

\[ T_i = \sum\limits_i \sigma_{ij} n_i \]

nebo v rozšířeném zápisu:

\[ T_1 = \sigma_{j1} n_j = \sigma_{11} n_1 + \sigma_{21} n_2 + \sigma_{31} n_3 \]

\[ T_2 = \sigma_{j1} n_j = \sigma_{12} n_1 + \sigma_{22} n_2 + \sigma_{32} n_3 \]

\[ T_3 = \sigma_{j1} n_j = \sigma_{13} n_1 + \sigma_{23} n_2 + \sigma_{33} n_3 \]

Příklad osově zatížené tyče (1D a 2D)

Uvažujme nejprve normálový řez tyčí s podélnou osou jako osou 1. Složky povrchových tahů jsou uvedeny na obrázku (2.1.7).

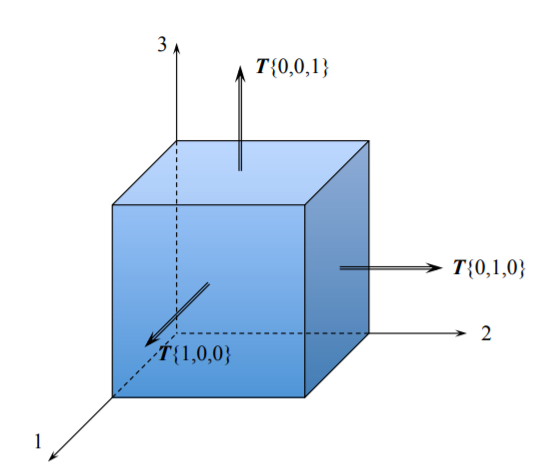
Dosazením hodnot složek obou vektorů do rovnice 2.1.13 získáme následující výrazy:

• rovina (1,0,0): $\( \sigma_0 = \sigma_{11}; 0 = \sigma_{21}; 0 = \sigma_{31} \)$

• rovina (0,1,0): $\( 0 = \sigma_{12}; 0 = \sigma_{22}; 0 = \sigma_{32} \)$

• rovina (0,0,1): $\( 0 = \sigma_{13}; 0 = \sigma_{23}; 0 = \sigma_{33} \)$

Složky matice napětí \(3 \times 3\) v globálním souřadném systému jsou tedy:

\[\begin{split} \boldsymbol{\sigma} = \begin{bmatrix} \sigma_0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{split}\]

To představuje jednoosý stav napětí.

Dvourozměrný příklad: Šikmý řez

V tomto případě se použije lokální souřadnicový systém otočený vzhledem k 3-osé ose. V tomto systému jsou složky \(n\) stejné jako v globálním systému. V daném řezu platí pro složky vektoru \(\vec{n}\)

\[ \vec{n} = [\cos \theta, \sin \theta, 0] \]

Dosazením výše uvedených hodnot do Cauchyho vzorce získáme:

\[ \vec{T}_n = [\sigma_0 \cos \theta, 0, 0] \]

kde složky jsou vyjádřeny v původní souřadnicové soustavě. Když chceme vyjádřit normálovou a smykovou složku napětí, musíme promítnout složky tensoru napětí do jednotlivých os, t.j. rozložit vektor napětí do dvou složek \([T_N, T_T]\).

\[T_N = \vec{T}_n \cdot \vec{n}\]

\[T_T = \vec{T}_n \cdot \vec{m}\]

kde \(\vec{m} \perp \vec{n}\), a tedy \(\vec{m} = [\sin \theta, -\cos \theta, 0]\)

\[T_N = \sigma_0 \cos^2 \theta\]

\[T_T = \sigma_0 \cos \theta \sin \theta \]

Symetrie tenzoru napětí

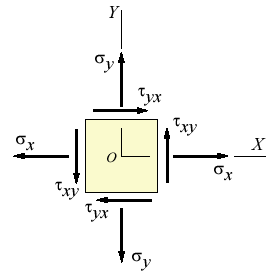
Symetrie tenzoru napětí vychází z rovnice momentové rovnováhy nekonečně malého objemového prvku.

Představme si nekonečně malý kvádr o stranách \(dx\), \(dy\) a \(dz\). Pro zjednodušení uvažujme momentovou rovnováhu kolem osy \(z\). Síly působící na stěny kolmé k osám \(x\) a \(y\) generují momenty kolem osy \(z\).

• Moment od napětí \(\sigma_{yx}\): \(M_y = \sigma_{yx} \, dx \, dy \, dz\)

• Moment od napětí \(\sigma_{xy}\): \(M_x = -\sigma_{xy} \, dx \, dy \, dz\)

Podmínka momentové rovnováhy kolem osy \(z\) (\(\sum M_z = 0\)) dává:

\(\sigma_{yx} \, dx \, dy \, dz - \sigma_{xy} \, dx \, dy \, dz = 0\)

Za předpokladu \(dx \, dy \, dz \neq 0\), z toho plyne:

\(\sigma_{xy} = \sigma_{yx}\)

Analogicky lze odvodit symetrii i pro ostatní složky tenzoru napětí z momentové rovnováhy kolem os \(x\) a \(y\):

• \(\sigma_{yz} = \sigma_{zy}\)

• \(\sigma_{xz} = \sigma_{zx}\)

Symetrie tenzoru napětí (\(\sigma_{ij} = \sigma_{ji}\)) je nutnou podmínkou pro momentovou rovnováhu nekonečně malého objemového prvku. Nerespektování této symetrie by vedlo k nenulovému výslednému momentu a tedy nekonečně velkému úhlovému zrychlení prvku, což je fyzikálně nemožné v statickém nebo kvazistatickém stavu.

Warning

Toto odvození platí za předpokladu absence objemových momentů působících na prvek. V inženýrských aplikacích je tento předpoklad obvykle splněn.

Symetrie tenzoru napětí vychází z rovnice momentové rovnováhy nekonečně malého objemového prvku. Obecně:

\[\sigma_{ij} = \sigma_{ji} \]

Tím se devět složek matice \(3 imes 3\) redukuje na pouhých šest nezávislých složek.

Speciální stavy napjatosti

a) Tah / Tlak

\[\begin{split} \boldsymbol{\sigma} = \begin{bmatrix} \sigma & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{split}\]

b) Rovinná napjatost

\[\begin{split} \boldsymbol{\sigma} = \begin{bmatrix} \sigma_{xx} & \tau_{xy} & 0 \\ \tau_{xy} & \sigma_{yy} & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{split}\]

Posunutí a deformace ve 3D

Note

Dodatečná informace - nebude součástí zkoušky

Vektor posunutí

\[\begin{split} \mathbf{u} = \begin{bmatrix} u(x,y,z) \\ v(x,y,z) \\ w(x,y,z) \end{bmatrix} \end{split}\]

Tenzor deformace

Definice tenzoru deformace \(\varepsilon_{ij}\) v mechanice kontinua popisuje lokální deformaci materiálu a je úzce spjata s polem posunutí \(\mathbf{u}\), jehož složky jsou \(u_i\) (kde \(i = 1, 2, 3\) odpovídá osám \(x_1, x_2, x_3\)).

Uvažujme nekonečně malý vektorový element \(d\mathbf{x}\) v nedeformovaném tělese, spojující dva blízké body s souřadnicemi \(x_i\) a \(x_i + dx_i\). Po deformaci se tyto body posunou o \(\mathbf{u}(x_i)\) a \(\mathbf{u}(x_i + dx_i)\), a vektorový element se transformuje na \(d\mathbf{x}'\).

Posunutí koncového bodu elementu \(d\mathbf{x}\) lze vyjádřit pomocí Taylorova rozvoje pole posunutí kolem počátečního bodu:

\[ u_i(x_j + dx_j) = u_i(x_j) + \frac{\partial u_i}{\partial x_j} dx_j + O((dx)^2) \]

Zanedbáme členy vyššího řádu, protože uvažujeme nekonečně malý element.

Deformovaný vektorový element \(d\mathbf{x}'\) spojuje body s souřadnicemi \(x_i + u_i(x_j)\) a \(x_i + dx_i + u_i(x_j + dx_j)\). Lze jej vyjádřit jako:

\[ dx'_i = (x_i + dx_i + u_i(x_j + dx_j)) - (x_i + u_i(x_j)) \]

\[ dx'_i = dx_i + u_i(x_j + dx_j) - u_i(x_j) \]

Dosazením Taylorova rozvoje pro \(u_i(x_j + dx_j)\):

\[ dx'_i = dx_i + \left( u_i(x_j) + \frac{\partial u_i}{\partial x_j} dx_j \right) - u_i(x_j) \]

\[ dx'_i = dx_i + \frac{\partial u_i}{\partial x_j} dx_j \]

Tento vztah lze zapsat v tenzorové notaci jako:

\[ dx'_i = (\delta_{ij} + \frac{\partial u_i}{\partial x_j}) dx_j = F_{ij} dx_j \]

kde \(F_{ij} = \delta_{ij} + \frac{\partial u_i}{\partial x_j}\) je tenzor gradientu deformace. Tento tenzor popisuje lineární transformaci nedeformovaného elementu \(d\mathbf{x}\) na deformovaný element \(d\mathbf{x}'\).

Pro kvantifikaci samotné deformace, tedy změny tvaru a velikosti, je užitečné zavést tenzor pravé míry deformace (Cauchy-Greenův tenzor deformace) \(\mathbf{C}\), definovaný jako:

\[ \mathbf{C} = \mathbf{F}^T \mathbf{F} \implies C_{ij} = F_{ki} F_{kj} = \left( \delta_{ki} + \frac{\partial u_k}{\partial x_i} \right) \left( \delta_{kj} + \frac{\partial u_k}{\partial x_j} \right) \]

\[ C_{ij} = \delta_{ij} + \frac{\partial u_j}{\partial x_i} + \frac{\partial u_i}{\partial x_j} + \frac{\partial u_k}{\partial x_i} \frac{\partial u_k}{\partial x_j} \]

Tenzor inženýrské míry deformace \(\mathbf{E}\) je definován jako rozdíl mezi deformovaným a nedeformovaným metrickým tenzorem (kterým je pro karteziánské souřadnice Kroneckerovo delta \(\delta_{ij}\)):

\[ \mathbf{E} = \frac{1}{2} (\mathbf{C} - \mathbf{I}) \implies E_{ij} = \frac{1}{2} (C_{ij} - \delta_{ij}) \]

Dosazením za \(C_{ij}\):

\[ E_{ij} = \frac{1}{2} \left( \delta_{ij} + \frac{\partial u_j}{\partial x_i} + \frac{\partial u_i}{\partial x_j} + \frac{\partial u_k}{\partial x_i} \frac{\partial u_k}{\partial x_j} - \delta_{ij} \right) \]

\[ E_{ij} = \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} + \frac{\partial u_k}{\partial x_i} \frac{\partial u_k}{\partial x_j} \right) \]

Pro malé deformace, kdy jsou gradienty posunutí \(\frac{\partial u_k}{\partial x_i}\) malé ve srovnání s jedničkou, lze zanedbat kvadratický člen \(\frac{\partial u_k}{\partial x_i} \frac{\partial u_k}{\partial x_j}\). V tomto případě se tenzor inženýrské míry deformace redukuje na tenzor malých deformací nebo linearizovaný tenzor deformace \(\varepsilon_{ij}\):

\[ \varepsilon_{ij} \approx \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \]

Tato definice, kterou jste uvedl, je tedy linearizovanou definicí tenzoru deformace, platnou pro případy malých deformací. Představuje symetrickou část gradientu posunutí. Symetrická část souvisí se změnou tvaru a velikosti, zatímco antisymetrická část (rotační tenzor) souvisí s rotací elementu bez změny jeho tvaru a velikosti v prvním řádu aproximace.

Složky tenzoru deformace

V trojrozměrném stavu napjatosti má symetrický tenzor deformace \(\boldsymbol{\varepsilon}\) druhého řádu v kartézských souřadnicích (x, y, z nebo \(x_1, x_2, x_3\)) následujících šest nezávislých složek:

Normálové deformace (diagonální složky):

• \(\varepsilon_{xx} = \varepsilon_{11} = \frac{\partial u_x}{\partial x} = \frac{\partial u_1}{\partial x_1}\): Poměrná změna délky elementu ve směru osy x.

• \(\varepsilon_{yy} = \varepsilon_{22} = \frac{\partial u_y}{\partial y} = \frac{\partial u_2}{\partial x_2}\): Poměrná změna délky elementu ve směru osy y.

• \(\varepsilon_{zz} = \varepsilon_{33} = \frac{\partial u_z}{\partial z} = \frac{\partial u_3}{\partial x_3}\): Poměrná změna délky elementu ve směru osy z.

Smykové deformace (nediagonální složky):

Tenzorové smykové deformace (\(\varepsilon_{ij}\) pro \(i \neq j\)) souvisejí s poloviční změnou úhlu mezi původně kolmými liniovými elementy. Inženýrská smyková deformace (\(\gamma_{ij}\)) je \(\gamma_{ij} = 2 \varepsilon_{ij}\).

• \(\varepsilon_{xy} = \varepsilon_{yx} = \varepsilon_{12} = \varepsilon_{21} = \frac{1}{2} \left( \frac{\partial u_x}{\partial y} + \frac{\partial u_y}{\partial x} \right) = \frac{1}{2} \gamma_{xy}\): Polovina změny úhlu mezi původně kolmými liniemi ve směrech x a y.

• \(\varepsilon_{yz} = \varepsilon_{zy} = \varepsilon_{23} = \varepsilon_{32} = \frac{1}{2} \left( \frac{\partial u_y}{\partial z} + \frac{\partial u_z}{\partial y} \right) = \frac{1}{2} \gamma_{yz}\): Polovina změny úhlu mezi původně kolmými liniemi ve směrech y a z.

• \(\varepsilon_{zx} = \varepsilon_{xz} = \varepsilon_{31} = \varepsilon_{13} = \frac{1}{2} \left( \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z} \right) = \frac{1}{2} \gamma_{zx}\): Polovina změny úhlu mezi původně kolmými liniemi ve směrech z a x.

kde \(u_x, u_y, u_z\) (nebo \(u_1, u_2, u_3\)) jsou složky vektoru posunutí.

Maticově lze tenzor deformace zapsat jako:

\[\begin{split} \boldsymbol{\varepsilon} = \begin{pmatrix} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz} \\ \varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz} \end{pmatrix} = \begin{pmatrix} \frac{\partial u_x}{\partial x} & \frac{1}{2} \left( \frac{\partial u_x}{\partial y} + \frac{\partial u_y}{\partial x} \right) & \frac{1}{2} \left( \frac{\partial u_x}{\partial z} + \frac{\partial u_z}{\partial x} \right) \\ \frac{1}{2} \left( \frac{\partial u_y}{\partial x} + \frac{\partial u_x}{\partial y} \right) & \frac{\partial u_y}{\partial y} & \frac{1}{2} \left( \frac{\partial u_y}{\partial z} + \frac{\partial u_z}{\partial y} \right) \\ \frac{1}{2} \left( \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z} \right) & \frac{1}{2} \left( \frac{\partial u_z}{\partial y} + \frac{\partial u_y}{\partial z} \right) & \frac{\partial u_z}{\partial z} \end{pmatrix} \end{split}\]

Warning

Tato definice platí pro malé deformace.

Hookeův zákon

Pro lineárně elastický materiál platí Hookův zákon v trojrozměrné podobě:

\[\varepsilon_x = \frac{1}{E} [\sigma_x - \nu (\sigma_y + \sigma_z)]\]

\[\varepsilon_y = \frac{1}{E} [\sigma_y - \nu (\sigma_x + \sigma_z)]\]

\[\varepsilon_z = \frac{1}{E} [\sigma_z - \nu (\sigma_x + \sigma_y)]\]

\[\gamma_{xy} = \frac{\tau_{xy}}{G}\]

\[\gamma_{yz} = \frac{\tau_{yz}}{G}\]

\[\gamma_{zx} = \frac{\tau_{zx}}{G}\]

kde

• \(E\) je Youngův modul pružnosti,

• \(\nu\) je Poissonovo číslo a

• \(G = \frac{E}{2(1+\nu)}\) je modul pružnosti ve smyku.

Obecný lineárně pružný materiál

V lineárně elastickém materiálu popisuje Hookův zákon vztah mezi tenzorem napětí \(\boldsymbol{\sigma}\) a tenzorem deformace \(\boldsymbol{\varepsilon}\). V obecném trojrozměrném stavu napjatosti a deformace lze tento vztah vyjádřit v tenzorové formě jako:

\[ \boldsymbol{\varepsilon} = \mathbf{S} : \boldsymbol{\sigma} \]

kde \(\mathbf{S}\) je tenzor poddajnosti (často se značí také jako \(\mathbf{C}^{-1}\), kde \(\mathbf{C}\) je tenzor tuhosti). Dvojtečka (\(:\)) značí dvojitou kontrakci tenzorů.

V maticové formě, při použití Voigtovy notace pro vektor napětí \(\{\sigma\} = [\sigma_x, \sigma_y, \sigma_z, \tau_{xy}, \tau_{yz}, \tau_{zx}]^T\) a vektor deformace \(\{\varepsilon\} = [\varepsilon_x, \varepsilon_y, \varepsilon_z, \gamma_{xy}, \gamma_{yz}, \gamma_{zx}]^T\), se Hookův zákon zapisuje jako:

\[\begin{split} \begin{pmatrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{pmatrix} = \begin{pmatrix} S_{11} & S_{12} & S_{13} & S_{14} & S_{15} & S_{16} \\ S_{21} & S_{22} & S_{23} & S_{24} & S_{25} & S_{26} \\ S_{31} & S_{32} & S_{33} & S_{34} & S_{35} & S_{36} \\ S_{41} & S_{42} & S_{43} & S_{44} & S_{45} & S_{46} \\ S_{51} & S_{52} & S_{53} & S_{54} & S_{55} & S_{56} \\ S_{61} & S_{62} & S_{63} & S_{64} & S_{65} & S_{66} \end{pmatrix} \begin{pmatrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{pmatrix} \end{split}\]

Matice poddajnosti \([S]\) je symetrická, což znamená \(S_{ij} = S_{ji}\), a má tedy maximálně 21 nezávislých konstant pro obecně anizotropní materiál.

Pro izotropní materiál (jehož vlastnosti jsou stejné ve všech směrech) se matice poddajnosti výrazně zjednodušuje a je vyjádřena pomocí dvou nezávislých materiálových konstant, Youngova modulu pružnosti (\(E\)) a Poissonova čísla (\(\nu\)), nebo pomocí Youngova modulu (\(E\)) a modulu pružnosti ve smyku (\(G = \frac{E}{2(1+\nu)}\)), případně pomocí Laméových konstant (\(\lambda\) a \(\mu = G\)). Matice poddajnosti pro izotropní materiál má tvar:

\[\begin{split} [S] = \begin{pmatrix} 1/E & -\nu/E & -\nu/E & 0 & 0 & 0 \\ -\nu/E & 1/E & -\nu/E & 0 & 0 & 0 \\ -\nu/E & -\nu/E & 1/E & 0 & 0 & 0 \\ 0 & 0 & 0 & 1/G & 0 & 0 \\ 0 & 0 & 0 & 0 & 1/G & 0 \\ 0 & 0 & 0 & 0 & 0 & 1/G \end{pmatrix} \end{split}\]

kde diagonální prvky souvisejí s normálovými deformacemi vyvolanými normálovými napětími a nediagonální prvky (mimo nuly) souvisejí s příčnými deformacemi (Poissonův jev) a smykovými deformacemi vyvolanými smykovými napětími.

\[\begin{split} [S] = \frac{1}{E} \begin{bmatrix} 1 & -\nu & -\nu & 0 & 0 & 0 \\ -\nu & 1 & -\nu & 0 & 0 & 0 \\ -\nu & -\nu & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2(1+\nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2(1+\nu) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2(1+\nu) \end{bmatrix} \end{split}\]

11. Matice tuhosti

\[\begin{split} [K] = \frac{E}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1-\nu & \nu & \nu & 0 & 0 & 0 \\ \nu & 1-\nu & \nu & 0 & 0 & 0 \\ \nu & \nu & 1-\nu & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1-2\nu}{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1-2\nu}{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1-2\nu}{2} \end{bmatrix} \end{split}\]

Hlavní napětí

Uvažujme rovinný stav napětí (2D), kde je tenzor napětí \(\boldsymbol{\sigma}\) redukován na matici 2x2:

\[\begin{split} \boldsymbol{\sigma} = \begin{pmatrix} \sigma_x & \tau_{xy} \\ \tau_{yx} & \sigma_y \end{pmatrix} \end{split}\]

Vlivem momentové rovnováhy platí \(\tau_{xy} = \tau_{yx}\), takže tenzor napětí je symetrický.

Hlavní napětí (\(\sigma_1, \sigma_2\)) jsou vlastní čísla tenzoru napětí. Lze je nalézt řešením charakteristické rovnice:

\[ \det(\boldsymbol{\sigma} - \lambda \mathbf{I}) = 0 \]

kde \(\lambda\) představuje hlavní napětí a \(\mathbf{I}\) je jednotková matice 2x2. Rozepsáním determinantu:

\[\begin{split} \det \begin{pmatrix} \sigma_x - \lambda & \tau_{xy} \\ \tau_{xy} & \sigma_y - \lambda \end{pmatrix} = (\sigma_x - \lambda)(\sigma_y - \lambda) - (\tau_{xy})^2 = 0 \end{split}\]

Rozvinutím této rovnice dostaneme kvadratickou rovnici pro \(\lambda\):

\[ \lambda^2 - (\sigma_x + \sigma_y) \lambda + (\sigma_x \sigma_y - \tau_{xy}^2) = 0 \]

Řešení této kvadratické rovnice pomocí vzorce pro kořeny dává hlavní napětí \(\sigma_1\) a \(\sigma_2\):

\[ \lambda_{1,2} = \frac{(\sigma_x + \sigma_y) \pm \sqrt{(\sigma_x + \sigma_y)^2 - 4(\sigma_x \sigma_y - \tau_{xy}^2)}}{2} \]

\[ \lambda_{1,2} = \frac{(\sigma_x + \sigma_y) \pm \sqrt{\sigma_x^2 + 2\sigma_x \sigma_y + \sigma_y^2 - 4\sigma_x \sigma_y + 4\tau_{xy}^2}}{2} \]

\[ \lambda_{1,2} = \frac{(\sigma_x + \sigma_y) \pm \sqrt{\sigma_x^2 - 2\sigma_x \sigma_y + \sigma_y^2 + 4\tau_{xy}^2}}{2} \]

\[ \lambda_{1,2} = \frac{(\sigma_x + \sigma_y) \pm \sqrt{(\sigma_x - \sigma_y)^2 + (2\tau_{xy})^2}}{2} \]

Označme hlavní napětí jako \(\sigma_1\) a \(\sigma_2\):

\[ \sigma_1 = \frac{(\sigma_x + \sigma_y)}{2} + \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \]

\[ \sigma_2 = \frac{(\sigma_x + \sigma_y)}{2} - \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \]

Nyní zavedeme průměrné normálové napětí \(\sigma_m\) a poloměr kružnice \(R\):

\[ \sigma_m = \frac{\sigma_x + \sigma_y}{2} \]

\[ R = \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \]

Pomocí těchto definic lze hlavní napětí zapsat jako:

\[ \sigma_1 = \sigma_m + R \]

\[ \sigma_2 = \sigma_m - R \]

Nyní se zaměřme na napětí (\(\sigma_n, \tau_t\)) působící na rovinu otočenou o úhel \(\theta\) od osy \(x\). Transformace napětí pro rovinný stav napětí je dána rovnicemi:

\[ \sigma_n = \frac{\sigma_x + \sigma_y}{2} + \frac{\sigma_x - \sigma_y}{2} \cos(2\theta) + \tau_{xy} \sin(2\theta) \]

\[ \tau_t = -\frac{\sigma_x - \sigma_y}{2} \sin(2\theta) + \tau_{xy} \cos(2\theta) \]

Naším cílem je ukázat, že body \((\sigma_n, \tau_t)\) leží na kružnici v rovině \(\sigma - \tau\). Přeuspořádejme transformační rovnice:

\[ \sigma_n - \frac{\sigma_x + \sigma_y}{2} = \frac{\sigma_x - \sigma_y}{2} \cos(2\theta) + \tau_{xy} \sin(2\theta) \]

\[ \tau_t = -\frac{\sigma_x - \sigma_y}{2} \sin(2\theta) + \tau_{xy} \cos(2\theta) \]

Nyní umocníme obě rovnice na druhou a sečteme je:

\[ \left(\sigma_n - \frac{\sigma_x + \sigma_y}{2}\right)^2 + \tau_t^2 = \left( \frac{\sigma_x - \sigma_y}{2} \cos(2\theta) + \tau_{xy} \sin(2\theta) \right)^2 + \left( -\frac{\sigma_x - \sigma_y}{2} \sin(2\theta) + \tau_{xy} \cos(2\theta) \right)^2 \]

Rozvinutím pravé strany:

\[ \left(\frac{\sigma_x - \sigma_y}{2}\right)^2 \cos^2(2\theta) + \tau_{xy}^2 \sin^2(2\theta) + 2 \frac{\sigma_x - \sigma_y}{2} \tau_{xy} \cos(2\theta) \sin(2\theta) + \left(\frac{\sigma_x - \sigma_y}{2}\right)^2 \sin^2(2\theta) + \tau_{xy}^2 \cos^2(2\theta) - 2 \frac{\sigma_x - \sigma_y}{2} \tau_{xy} \sin(2\theta) \cos(2\theta) \]

Střední členy se odečtou a zbývá:

\[ \left(\frac{\sigma_x - \sigma_y}{2}\right)^2 (\cos^2(2\theta) + \sin^2(2\theta)) + \tau_{xy}^2 (\sin^2(2\theta) + \cos^2(2\theta)) \]

Použitím goniometrické identity \(\sin^2(\alpha) + \cos^2(\alpha) = 1\) dostaneme:

\[ \left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2 \]

Levá strana rovnice je:

\[ \left(\sigma_n - \frac{\sigma_x + \sigma_y}{2}\right)^2 + \tau_t^2 \]

Spojením obou stran:

\[ \left(\sigma_n - \frac{\sigma_x + \sigma_y}{2}\right)^2 + \tau_t^2 = \left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2 \]

Substitucí dříve definovaného průměrného normálového napětí \(\sigma_m = \frac{\sigma_x + \sigma_y}{2}\) a poloměru kružnice \(R = \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}\) dostaneme rovnici kružnice:

\[ (\sigma_n - \sigma_m)^2 + \tau_t^2 = R^2 \]

Tato rovnice představuje Mohrovu kružnici v rovině \(\sigma - \tau\), kde:

• Střed kružnice leží na ose normálového napětí \(\sigma\) v bodě \((\sigma_m, 0) = \left(\frac{\sigma_x + \sigma_y}{2}, 0\right)\).

• Poloměr kružnice je \(R = \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}\).

Hlavní napětí \(\sigma_1\) a \(\sigma_2\) odpovídají průsečíkům Mohrovy kružnice s osou normálového napětí (\(\tau_t = 0\)), kde \(\sigma_n = \sigma_m \pm R\). Maximální smykové napětí \(\tau_{max}\) odpovídá hornímu a dolnímu bodu kružnice a má velikost rovnou poloměru \(R\):

\[ \tau_{max} = R = \sqrt{\left(\frac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} = \frac{\sigma_1 - \sigma_2}{2} \]

Tímto jsme odvodili rovnici Mohrovy kružnice jako geometrickou reprezentaci hlavních čísel (a obecně transformovaných složek) tenzoru napětí ve 2D.

Hlavní napětí a deformace ve 3D

Podobně můžeme postupovat ve třech rozměrech.

\[ \det(\boldsymbol{\sigma} - \lambda \mathbf{I}) = 0 \]

\[ \det(\boldsymbol{\varepsilon} - \lambda \mathbf{I}) = 0 \]

V tomto případě platí, že řešení determinantu vede na kubickou rovnici, která má tři řešení: tři hlavní napětí \(\sigma_1, \sigma_2, \sigma_3\) nebo \(\epsilon_1, \epsilon_2, \epsilon_3\).

Objemová deformace je stopou tenzoru deformace

Uvažujme infinitezimální objemový element ve tvaru kvádru s počátečními rozměry \(dx_1, dx_2, dx_3\). Jeho počáteční objem je \(dV_0 = dx_1 \, dx_2 \, dx_3\).

Po deformaci se rozměry elementu změní. Pro malé deformace můžeme změnu délky hrany ve směru osy \(x_i\) aproximovat jako \((1 + \varepsilon_{ii}) dx_i\), kde \(\varepsilon_{ii}\) je normálová složka tenzoru deformace ve směru \(x_i\).

Deformované rozměry elementu jsou tedy přibližně:

• \(dx'_1 = (1 + \varepsilon_{11}) dx_1\)

• \(dx'_2 = (1 + \varepsilon_{22}) dx_2\)

• \(dx'_3 = (1 + \varepsilon_{33}) dx_3\)

Objem deformovaného elementu \(dV\) je dán součinem těchto deformovaných rozměrů (zanedbáváme členy vyšších řádů pro malé deformace):

\[ dV = dx'_1 \, dx'_2 \, dx'_3 = (1 + \varepsilon_{11}) dx_1 \, (1 + \varepsilon_{22}) dx_2 \, (1 + \varepsilon_{33}) dx_3 \]

\[ dV = (1 + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} + \text{členy vyšších řádů}) \, dx_1 \, dx_2 \, dx_3 \]

Pro malé deformace zanedbáme členy vyšších řádů:

\[ dV \approx (1 + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}) \, dV_0 \]

Objemová deformace \(\varepsilon_v\) je definována jako relativní změna objemu:

\[ \varepsilon_v = \frac{dV - dV_0}{dV_0} = \frac{(1 + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}) dV_0 - dV_0}{dV_0} \]

\[ \varepsilon_v = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} \]

Stopa tenzoru deformace \(\text{Tr}(\boldsymbol{\varepsilon})\) je součet jeho diagonálních prvků:

\[ \text{Tr}(\boldsymbol{\varepsilon}) = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} \]

Porovnáním obou výrazů dostáváme:

\[ \varepsilon_v = \text{Tr}(\boldsymbol{\varepsilon}) \]

Tím jsme prokázali, že pro malé deformace je objemová deformace rovna stopě tenzoru deformace.

Objemová složka napětí a objemový modul pružnosti

Objemový modul pružnosti \(K\) charakterizuje odpor materiálu ke změně objemu při rovnoměrném všesměrném zatížení (hydrostatickém tlaku). Je definován jako poměr mezi objemovou složkou napětí (\(\sigma_m\)) a objemovou deformací (\(\varepsilon_v\)):

\[ K = \frac{\sigma_m}{\varepsilon_v} \]

Pro lineárně elastický izotropní materiál platí Hookův zákon:

\[\begin{split} \varepsilon_{xx} = \frac{1}{E} [\sigma_{xx} - \nu (\sigma_{yy} + \sigma_{zz})] \\ \varepsilon_{yy} = \frac{1}{E} [\sigma_{yy} - \nu (\sigma_{xx} + \sigma_{zz})] \\ \varepsilon_{zz} = \frac{1}{E} [\sigma_{zz} - \nu (\sigma_{xx} + \sigma_{yy})] \end{split}\]

kde \(E\) je Youngův modul pružnosti a \(\nu\) je Poissonovo číslo.

Objemová deformace \(\varepsilon_v\) je stopou tenzoru deformace:

\[ \varepsilon_v = \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \]

Sečtením rovnic Hookova zákona pro normálové deformace dostaneme:

\[ \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} = \frac{1}{E} [(\sigma_{xx} + \sigma_{yy} + \sigma_{zz}) - 2\nu (\sigma_{xx} + \sigma_{yy} + \sigma_{zz})] \]

\[ \varepsilon_v = \frac{1}{E} (1 - 2\nu) (\sigma_{xx} + \sigma_{yy} + \sigma_{zz}) \]

Objemová složka napětí \(\sigma_m\) (pro hydrostatické zatížení \(\sigma_{xx} = \sigma_{yy} = \sigma_{zz} = -p\), kde \(p\) je tlak, ale obecně):

\[ \sigma_m = \frac{1}{3} (\sigma_{xx} + \sigma_{yy} + \sigma_{zz}) \]

Z rovnice pro objemovou deformaci vyjádříme součet normálových napětí:

\[ \sigma_{xx} + \sigma_{yy} + \sigma_{zz} = E \frac{\varepsilon_v}{1 - 2\nu} \]

Dosadíme tento výraz do definice objemové složky napětí:

\[ \sigma_m = \frac{1}{3} \left( E \frac{\varepsilon_v}{1 - 2\nu} \right) \]

Nyní použijeme definici objemového modulu pružnosti \(K = \frac{\sigma_m}{\varepsilon_v}\):

\[ K = \frac{\frac{1}{3} E \frac{\varepsilon_v}{1 - 2\nu}}{\varepsilon_v} \]

Po zkrácení \(\varepsilon_v\) získáme výsledný vztah:

\[ K = \frac{E}{3(1 - 2\nu)} \]

\[ \varepsilon_v = \text{Tr}(\boldsymbol{\varepsilon}) \]

Další informace a reference

• Detailní popis transformace a vyjádření vektorů napětí v rovině je možné najít na odkazu z MIT David Roylance: Transformation of Stresses and Strains.

• Popis tenzoru je možné najít v kapitole z TU Delft.

• Tato kapitola částečně vychází z textu Stress Tensor, Tomasz Wierzbicki, Massachusetts Institute of Technology via MIT OpenCourseWare