Fiktivní síly

V učebnicích se často tvrdí, že “odstředivá síla neexistuje”. Když satelit obíhá Zemi, není udržován v rovnováze mezi dvěma stejnými a opačnými silami, tedy gravitací směřující k Zemi a odstředivou silou směřující ven. Satelit má tentenci pohyvoat se přímočaře a existuje pouze jedna síla, gravitační, která zakřivuje jeho dráhu.

Note

Slovo centrifugální (odstředivý) pochází z latinských slov centrum, “střed,” a fugere, “utíkat,” takže slovo znamená “utíkající od středu.” Odstředivou sílu studovali fyzikové již v roce 1629 a samotný termín používal Sir Isaac Newton ve své latinské podobě vis centrifuga v roce 1687.

Na druhé straně, dostředivou sílu moc necítíme ale když autem projedeme zatáčku příliš rychle a cítíme se odmrštěni od středu zakřivení naší dráhy, a tedy působí na nás “odstředivá síla” se zdá být velmi reálná. Celý problém, který nastal je v popisu naěho vztažného systému.

Inerciální vztažná soustava

Jako inerciální vztažná soustava se označuje taková vztažná soustava, v níž platí zákon setrvačnosti. Každá vztažná soustava, je-li vzhledem k dané inerciální soustavě v klidu nebo pohybu rovnoměrném přímočarém, je rovněž inerciální. Soustavy, v nichž zákon setrvačnosti neplatí, se nazývají neinerciální. Pohybují se pohybem přímočarým zrychleným, zpožděným, nebo křivočarými pohyby.

D´Alembertův princip

Podívejme se na jednodušší příklad, který nezahrnuje rotaci. Auto zrychluje zrychlením \(\vec{a}\) doprava.

Závěsné olovnice v autě se kvůli zrychlení nenachází ve vertikální poloze. Někdo by řekl, že na olovnici působí pouze dvě síly – její váha a tah v provázku – a v důsledku toho olovnice zrychluje doprava. Pomocí vztahu \(\vec{F}=m\vec{a}\) lze snadno najít tah v provázku a úhel, který provázek svírá s vertikálou.

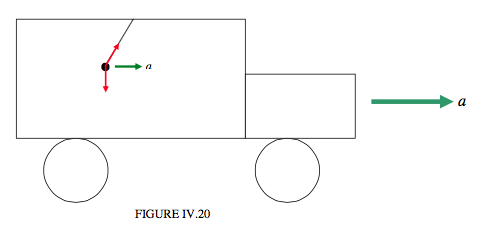
Nicméně, cestující v autě vidí věci jinak. Pro cestujícího v autě se nic nezrychluje. Olovnice je pouze ve statické rovnováze působením tří sil, z nichž jedna je síla \(ma\) doleva.

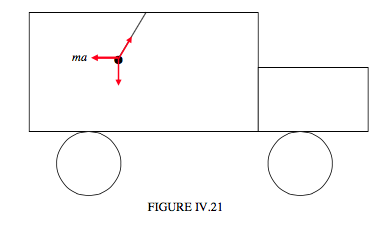
Zdá se, že ve vztažné soustavě vně auta existují pouze dvě síly, ale ve zrychlující vztažné soustavě uvnitř auta lze systém dokonale popsat postulováním existence síly \(ma\) táhnoucí doleva. Toto je princip klasické mechaniky, známý jako d’Alembertův princip, kdy, pokud popíšeme systém ve zrychlující vztažné soustavě, můžeme zrychlení nahradit silou v opačném směru. D’Alembertův princip, alternativní formulace druhého Newtonova pohybového zákona, byla formulovaná francouzským polymathou 18. století Jeanem Le Rondem d’Alembertem. V podstatě princip redukuje problém v dynamice na problém ve statice. Druhý zákon říká, že síla \(F\) působící na těleso se rovná součinu hmotnosti \(m\) a zrychlení a tělesa, nebo \(F = ma\); v d’Alembertově formě se síla \(F\) plus zápor hmotnosti \(m\) krát zrychlení a tělesa rovná nule: \(F − ma = 0\). Jinými slovy, těleso je v rovnováze pod působením skutečné síly F a fiktivní síly −ma. Fiktivní síla se také nazývá setrvačná síla a obrácená efektivní síla.

D’Alembertův princip říká, že součet všech sil působících na systém, včetně setrvačných sil, se rovná nule. Setrvačné síly jsou fiktivní síly, které se objevují v neinerciálních (zrychlujících nebo rotujících) referenčních rámcích.

Matematicky se dá D’Alembertův princip vyjádřit jako:

\[\sum (\vec{F}_i - m_i \vec{a}_i) \cdot \delta \vec{r}_i = 0\]

kde:

• \(\vec{F}_i\) je výsledná vnější síla působící na i-tou částici.

• \(m_i\) je hmotnost i-té částice.

• \(\vec{a}_i\) je zrychlení i-té částice.

• \(\delta \vec{r}_i\) je virtuální posunutí i-té částice.

Představte si blok na nakloněné rovině. Podle druhého Newtonova zákona se blok zrychluje dolů po rovině v důsledku gravitační síly.

Inerciální referenční rámec (Newtonův zákon)

• Síly působící na blok:

  • Gravitační síla (\(\vec{F}_g\))

  • Normálová síla (\(\vec{N}\))

  • Třecí síla (\(\vec{F}_f\))

• Výsledná síla způsobuje zrychlení bloku (\(\vec{a}\)).

Neinerciální referenční rámec (D’Alembertův princip)

• Síly působící na blok:

  • Gravitační síla (\(\vec{F}_g\))

  • Normálová síla (\(\vec{N}\))

  • Třecí síla (\(\vec{F}_f\))

  • Setrvačná síla (\(\vec{F}_i = -m\vec{a}\))

• Podle D’Alembertova principu je součet těchto sil nulový, což znamená, že blok je v rovnováze.

D’Alembertův princip je důležitý, protože:

• Umožňuje řešit složité dynamické problémy pomocí metod statiky.

• Je základem Lagrangeovy mechaniky, která je výkonným nástrojem pro analýzu složitých mechanických systémů.

• Pomáhá pochopit koncept setrvačných sil a jejich vliv na pohyb.

Podobná situace je s odstředivou silou. Pokud uvažujete satelit na oběžné dráze kolem Země, někteří by řekli, že na satelit působí pouze jedna síla, gravitační síla směrem k Zemi. Satelit, který je na kruhové oběžné dráze, zrychluje směrem ke středu kruhu a vše je, jak se očekávalo - \(F=ma\). Zrychlení je dostředivé zrychlení. Astronaut na palubě satelitu může mít jiný pohled. Je v konstantní vzdálenosti od Země, nezrychluje; je ve statické rovnováze a necítí na sobě žádnou výslednou sílu – cítí se beztížný. Pokud byl naučen, že Země vyvíjí gravitační sílu, pak to musí být vyváženo silou směřující od Země. Tato síla, která se projeví při popisu v rotující vztažné soustavě, je odstředivá síla.

Rotující souřadnicové systémy

• \(\Sigma = Oxyz\) je inerciální vztažná soustava (nezrychluje ani nerotuje).

• \(\Sigma' = Ox'y'z'\) je vztažná soustava, která rotuje kolem osy \(z\) s úhlovou rychlostí \(\vec{\omega} = \omega \vec{k}\).

Tři otázky:

1. Pokud je bod P pevný vzhledem k \(\Sigma'\), jaká je jeho rychlost \(v\) vzhledem k \(\Sigma\)?

2. Pokud se bod P pohybuje rychlostí \(v'\) vzhledem k \(\Sigma'\), jaká je jeho rychlost \(v\) vzhledem k \(\Sigma\)?

3. Pokud má bod P zrychlení \(a'\) vzhledem k \(\Sigma'\), jaké je jeho zrychlení \(a\) vzhledem k \(\Sigma\)?

Uvažujme jednoduchý 2D problém, kdy osy \(z\) jsou stejné a systém se otáčí rychlostí \(\vec{\omega}\)

1. Odpověď na první otázku je:

   \[\vec{v} = \vec{\omega} \times \vec{r}\]

2. Pokud se P pohybuje rychlostí \(v'\) vzhledem k \(\Sigma'\), pak jeho rychlost \(v\) vzhledem k \(\Sigma\) je:

   \[\vec{v} = \vec{v}' + \vec{\omega} \times \vec{r}\]

   nebo

   \[\dot{\vec{r}} = \dot{\vec{r}}' + \vec{\omega} \times \vec{r}\]

   Toto ukazuje, že:

   \[\left(\frac{d}{dt}\right)_\Sigma = \left(\frac{d}{dt}\right)_{\Sigma'} + \vec{\omega} \times\]

3. Pokud P zrychluje vzhledem k \(\Sigma'\), můžeme použít operátor k rovnici:

   \[{\vec{a}} = (\frac{d}{dt})_{ \Sigma^{\prime}} ({\vec v}^{\prime} + \vec \omega \times {\vec r}) + \vec \omega \times ({\vec v}^{\prime} + \vec \omega \times {\vec r}) \]

\[= {\vec a}^{\prime} +\vec \omega \times \vec v^{\prime} + \vec \omega \times \vec v^{\prime} + \vec \omega \times ( \vec \omega \times {\vec r} ).\]

\[\vec{a} = {\vec a}^{\prime} + \vec \omega \times( \vec \omega \times {\vec r}) + 2 \vec \omega\times \vec{v^{\prime}}\]

Pokud P nezrychluje ani se nepohybuje vzhledem k \(\Sigma'\), pak:

\[a = \omega \times (\omega \times r)\]

Což je dostředivé zrychlení jak můžeme lehce dokázat podle \({\bf A} \times({ \bf B} \times { \bf C} )=({ \bf A} \cdot { \bf C)B-(A\cdot B)C}\).

\[\vec a = \vec \omega \times (\vec \omega \times \vec r) = (\vec \omega \cdot \vec r)\vec \omega - \omega^2 \vec r\]

Pokud se částice pohybuje rychlostí \(\vec v'\) vzhledem k \(\Sigma'\), má dodatečné zrychlení \(2\vec \omega \times \vec v'\) vzhledem k \(\Sigma\), což je Coriolisovo zrychlení.

Inverzní rovnice je:

\[\vec a' = \vec a + \vec \omega \times (\vec r \times \vec \omega) + 2\vec v' \times \vec \omega\]

\[\vec F' = \vec F + m\vec \omega \times (\vec r \times \vec \omega) + 2m \vec v' \times \vec \omega\]

Coriolisova síla:

\[F = 2m\vec v' \times \vec \omega\]

Coriolisova síla - myšlenkový experiment

Nyní si představte myšlenkový experiment (Gedanken Prüfung). Jděte na rovník a postavte vysokou věž. Pusťte z vrcholu věže kámen. Zamyslete se nad směrem vektoru \(2m\vec{v}' \times \vec{\omega}\). Opravdu se nad tím zamyslete. Nebo se zamyslete nad zákonem zachování momentu hybnosti. Kámen padá blíže k ose rotace Země. Musí zachovat moment hybnosti. Padá východně od věže (nikoli západně!).

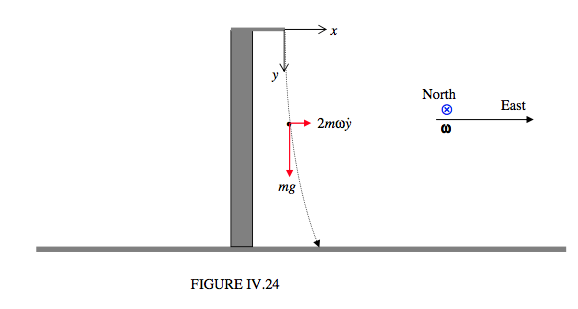
Na kámen působí dvě síly: jeho tíha \(mg\) a Coriolisova síla. Vektor rotace Země \(\vec{\omega}\) směřuje k severu. Coriolisova síla je kolmá k rychlosti kamene. Rozložíme-li rychlost kamene na svislou složku \(\dot{y}\) směřující dolů a vodorovnou složku \(\dot{z}\) směřující na východ, odpovídající složky Coriolisovy síly budou \(2m\omega\dot{y}\) na východ a \(2m\omega\dot{x}\) nahoru. Předpokládám však, že \(\dot{z} \ll \dot{y}\) a jedinou významnou Coriolisovou silou je složka \(2m\omega\dot{y}\) směřující na východ, kterou jsem nakreslil. Jiným způsobem, jak vyjádřit tuto aproximaci, je říci, že složka Coriolisovy síly směřující nahoru je zanedbatelná ve srovnání s tíhou \(mg\) kamene.

Po pádu po dobu \(t\) se souřadnice \(y\) kamene určí obvyklým způsobem:

\[\ddot{y} = g, \quad \dot{y} = gt, \quad y = \frac{1}{2}gt^2\]

A souřadnice \(x\) se určí z:

\[\ddot{x} = 2\omega\dot{y} = 2\omega gt, \quad \dot{x} = \omega gt^2, \quad x = \frac{1}{3}\omega gt^3\]

Takto můžete zjistit, jak daleko na východ kámen padl po dvou sekundách, nebo jak daleko na východ padl, pokud je výška věže 100 metrů. Rovnice trajektorie by byla \(t\)-eliminantou:

\[x^2 = \frac{8\omega^2}{9g}y^3\]

Pro Zemi je \(\omega = 7.292 \times 10^{-5} \, \text{rad s}^{-1}\) a na rovníku \(g = 9.780 \, \text{m s}^{-2}\), takže:

\[\frac{8\omega^2}{9g} = 4.788 \times 10^{-10} \, \text{m}^{-1}\]