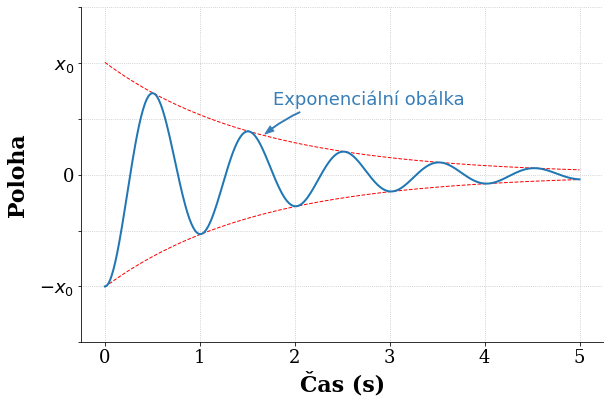
Tlumené vibrace

import numpy as np
from matplotlib import pyplot as plt

Rovnice pohybu

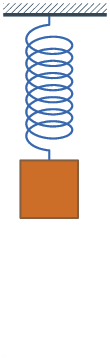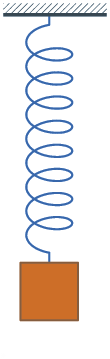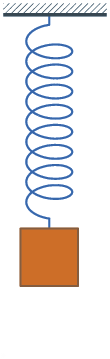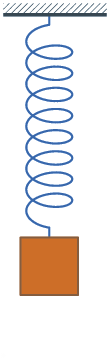
Pro odvození rovnice pohybu tlumených vibrací uvažujeme oscilátor s hmotností \(m\), tuhostí pružiny \(k\) a tlumicí silou úměrnou rychlosti, \(F_d\) = -bv\(, kde \)b$ je koeficient tlumení.

Podle druhého Newtonova zákona platí:

\[\sum F = m \ddot{x}\]

kde:

• \(\sum F\) je výsledná síla působící na oscilátor

• \(m\) je hmotnost oscilátoru

• \(a\) je zrychlení oscilátoru

Výsledná síla je součtem vratné síly pružiny a tlumicí síly:

\[\sum F = -kx - b \dot{x}\]

Dosazením do druhého Newtonova zákona dostaneme:

\[m \ddot{x} = -kx - b \dot{x}\]

\[m \ddot{x} + b \dot{x} + kx = 0\]

\[ \ddot{x} + \frac{b}{m} \dot{x} + \frac{k}{m} x = 0 \]

Tato rovnice je lineární, homogenní diferenciální rovnice druhého řádu s konstantními koeficienty. Určení typu diferenciální rovnice je důležité, protože přístup potřebný k jejímu řešení na něm závisí. K řešení diferenciálních rovnic tohoto typu se obvykle volí exponenciální ansatz.

Exponenciální řešení

Rovnice je homogenní lineární diferenciální rovnice druhého řádu s konstantními koeficienty. Předpokládá se, že řešením takové diferenciální rovnice je exponenciální funkce. Tuto metodu poprvé popsal Leonard Euler.

\[ x(t) = C e^{\lambda t}\]

Vytvořením první a druhé derivace získáme:

\[ \dot{x}(t) = \lambda C e^{\lambda t} \]

\[ \ddot{x}(t) = \lambda^2 C e^{\lambda t} \]

Dosazením těchto rovnic do diferenciální rovnice dostaneme:

\[ \lambda^2 C e^{\lambda t} + \frac{b}{m} \lambda C e^{\lambda t} + \frac{k}{m} C e^{\lambda t} = 0 \]

Dělením oběma stranami \(C e^{\lambda t}\) se vztah zjednoduší na:

\[ \lambda^2 + \frac{b}{m} \lambda + \frac{k}{m} = 0 \]

Tato rovnice se nazývá charakteristická rovnice. Je to kvadratická rovnice ve standardním tvaru, takže existují dvě řešení pro \(\lambda\):

\[ \lambda_{1,2} = - \frac{b}{2m} \pm \sqrt{\left( \frac{b}{2m} \right)^2 - \frac{k}{m}} \]

Pro další zjednodušení zavádíme nové konstanty \(\delta\) a \(\omega\):

\[ \delta = \frac{b}{2m}, \quad \omega_0 = \sqrt{\frac{k}{m}} \]

Rovnice se pak přepíše jako:

\[ \lambda_{1,2} = - \delta \pm \sqrt{\delta^2 - \omega_0^2} \]

Další řešení závisí na hodnotách \(\lambda_1\) a \(\lambda_2\). Je nutné zvážit několik různých možností. Výraz uvnitř druhé odmocniny se nazývá diskriminant. V závislosti na volbě konstant \(\delta\) a \(\omega_0\) může být diskriminant větší než 0, menší než 0 nebo roven 0. Proto \(\lambda_1\) a \(\lambda_2\) mohou být:

• Dvě různá reálná řešení.

• Dvě komplexně sdružená řešení.

• Dvě identická reálná řešení.

Každá z těchto možností vyžaduje jiný přístup k řešení. Obecné řešení homogenní diferenciální rovnice má tvar:

\[ x(t) = C_1 x_1(t) + C_2 x_2(t) \]

Funkce \(x_1(t)\) a \(x_2(t)\) jsou určeny hodnotou diskriminantu. Podívejme se nyní na různé možnosti.

Případ silně tlumený (overdamped) - aperiodický kmit

Pokud \(\delta > \omega_0\), máme případ silného tření. Diskriminant v rovnici je kladný a existují dvě různá reálná řešení pro \(\lambda\). Řešení diferenciální rovnice pak vypadá takto:

\[ x_1(t) = C_1 e^{\lambda_1 t} \]

\[ x_2(t) = C_2 e^{\lambda_2 t} \]

Dosazením do rovnice dostaneme obecné řešení diferenciální rovnice:

\[ x(t) = C_1 e^{(-\delta + \sqrt{\delta^2 - \omega_0^2}) t} + C_2 e^{(-\delta - \sqrt{\delta^2 - \omega_0^2}) t} \]

Při zjednodušení rovnice můžeme vložit nový konstantní člen:

\[ \alpha = \sqrt{\delta^2 - \omega_0^2} \]

Po dosazení do rovnice získáme:

\[ x(t) = e^{-\delta t} \left( C_1 e^{\alpha t} + C_2 e^{-\alpha t} \right) \]

Toto je řešení pro případ silného tlumení. Konstanty \(C_1\) a \(C_2\) pro konkrétní úlohu mohou být určeny z počátečních podmínek, jako je počáteční pozice a počáteční rychlost kyvadla.

\[ x(0) = x_0, \quad \dot{x}(0) = v_0 \]

Kritický případ tlumení - mezně aperiodický kmit

Mluvíme o kritickém tlumení, když \(\delta = \omega_0\). Jedná se o přechod od nadměrného tlumení k oscilaci. V tomto případě má rovnice jediné řešení pro \(\lambda\):

\[ \lambda_1 = \lambda_2 = \lambda = -\delta \]

Mohlo by se zdát, že v tomto případě máme jenom jedno řešení:

\[x_1(t) = C_1 e^{\lambda t} \]

Dané řešení ale není fyzikálně správné. Podle něho v čase \(t=0\) a při původní výchylce \(x_0\) je rychlost vždy rovna \(v_0 = v(0) = x_0 \lambda\). V podstatě ale v čase 0 můžeme umístnit oscilátor do libovolné polohy \(x_0\) s libovolnou rychlostí \(v_0\). Řěšení můžeme získat když uvážime silně tlumený případ, když \(\alpha \rightarrow 0\). Pro malé hodnoty \(\alpha\) můžeme napsat \(e^{\alpha t} = 1 + \alpha t \) a zároveň vztah $\( x(t) = e^{-\delta t} \left( C_1 e^{\alpha t} + C_2 e^{-\alpha t} \right) \)\( platí pro všechny \)C_1\( a \)C_2\(. Když si zvolíme \)C_2 = -C_1\( získáme \)\( x(t) = e^{-\delta t} \left( C_1 2 \alpha t \right) = t e^{\lambda t} (2 \alpha C_1) \)\( Protože pronásobením konstantou jenom změníme velikost neznámé konstanty \)C_1$ může pro druhé řešení napsat Použití exponenciálního řešení v tomto případě znamená použití následujícího postupu pro získání dvou dílčích řešení diferenciální rovnice:

\[ x_2(t) = t C_2 e^{\lambda t} \]

Vložení do obecného řešení nám dává řešení pro kritický případ tlumení:

\[ x(t) = e^{-\delta t} (C_1 + t C_2) \]

Integrační konstanty \(C_1\) a \(C_2\) musí být získány z počátečních podmínek konkrétního problému:

\[ x(0) = x_0 \quad,\quad \dot{x}(0) = v_0 \]

Podrobnosti pro výpočet konstant lze nalézt na Wolfram Alpha.

Tlumený harmonický kmit (underdamped)

Tlumená oscilace nastává pro \(\delta < \omega_0\). V tomto případě je diskriminant v rovnici záporný. Proto \(\lambda_1\) a \(lambda_2\) jsou komplexní čísla. Exponenciální funkce \((x(t)=C e^{\lambda t}\) je řešením diferenciální rovnice.

\[ x_1(t) = C_1 e^{\lambda_1 t} \]

\[ x_2(t) = C_2 e^{\lambda_2 t} \]

Vyjádření $\lambda získáme:

\[ x(t) = e^{-\delta t} \left( C_1 e^{\sqrt{\delta^2 - \omega_0^2}\; t} + C_2 e^{-\sqrt{\delta^2 - \omega_0^2}\; t}\right) \]

Dané řešení vyjádřuje kmoplexní čísla. protože v podtlumeném případě je termín pod odmocninou záporný. Když nahradíme výraz pod závorkou novou veličinou \(\omega_d\), získáme

\[ \omega_d = \sqrt{\omega_0^2 - \delta^2} \]

\[ \sqrt{\delta^2 - \omega_0^2} = \sqrt{-1 \cdot (\omega_0^2 - \delta) } = i \sqrt{\omega_0^2 - \delta^2} \tag{eq:iomega} \]

Jak uvidíme za chvíli, konstanta \(\omega_d\) představuje přirozenou frekvenci tlumeného harmonického oscilátoru. Řešení pohybové rovnice můžeme vyjádřit

\[ x(t) = e^{-\delta t} \left( {C_1 e^{i \omega_d t} + C_2 e^{- i \omega_d t}} \right) \]

Pro práci s komplexními čísly použijeme Eulerův vzorec, která spojuje komplexní exponenciální funkce s trigonometrickými funkcemi:

\[ e^{i \phi} = \cos \phi + i \sin \phi \]

\[ x(t) = e^{-\delta t} \left( C_1 \cos \omega_d t + i C_1 \sin \omega_d t + C_2 \cos_d \omega t - i C_2 \sin \omega_d t\right) \]

\[ x(t) = e^{-\delta t} \left( (C_1 + C_2) \cos \omega_d t + i (C_1-C_2) \sin \omega_d t \right) \]

\[ x(t) = e^{-\delta t} \left( C_3 \cos \omega_d t + C_4 \sin \omega_d t \right) \]

kde \(C_4\) je \(i (C_1-C_2)\). Ukázali jsme si, že součet dvojice harmonických kmitů se stejnou ferkevencí je možné vyjádřit jako jednou trigonometrickou funkcí, která obsahuje fázový posuv

\[ x(t) = e^{-\delta t} \left( A \cos \omega_d t + \psi \right) \]

kde

• \(\omega_d\) je tlumená vlastní frekvence

• konstanty \(A\) a \(\psi\) jsou amplituda a fáze a mohou být vypočteny z dané množiny počátečních podmínek.

\[ \omega_d = \sqrt{\omega_0^2 - \delta^2} = \sqrt{\omega_0^2 - \left(\frac{b}{2m}\right)^2} = \omega_0 \sqrt{1 - \left(\frac{b}{2m \omega_0}\right)^2} \]

Perioda tlumených kmitů je určena

\[ T_d = \frac{2\pi}{\omega_d} \]

a frekvence

\[ f_d = \frac{\omega_d}{2\pi} = f \sqrt{1 - \left(\frac{b}{2m \omega_0}\right)^2} \]

kde \(f\) je frekvence vlastních kmitů

Součinitel tlumení

Můžeme zavést veličinu, kterou označíme jako součinitel tlumení

\[ \zeta = \frac{b}{2m\omega_0}\]

V značení, které jsme používali v předcházejícím textu platí:

\[\sqrt{\delta^2 - \omega_0^2} = \omega_0 \sqrt{\zeta^2 - 1} \]

a tedy můžeme typ kmitů posoudit na základě hodnoty součinitele tlumení

1. \(\zeta > 1\) - aperiodický kmit

2. \(\zeta = 1\) - mezní aperiodický kmit

3. \(\zeta < 0\) - tlumené kmitání

Dodatečné informace

• Vizualizaci tlumeného kmitání s matematicky korektním odvozením je možné najít na https://beltoforion.de/en/harmonic_oscillator/.

Vizualizace

K vykreslení odezvy použijeme řešení diferenciální rovnici, kterou jsme odvodili. Řešení pro tlumený harmonický kmit je:

\[ x(t) = e^{-\zeta\omega_0t}\left(c_1 e^{i \omega_d t} + c_2 e ^{-i \omega_d t}\right) \]

\[ x(t) = e^{-\zeta\omega_0t}\left(a_1 \cos{\omega_d t} + a_2 \sin{\omega_d t}\right) \]

Abychom mohli tuto rovnici použít, musíme vyřešit pro \(c_1\) a \(c_2\) nebo \(a_1\) a \(a_2\) pomocí počátečních podmínek. Zde použijeme tvar sin/cos. Řešením rovnice pro obecnou počáteční rychlost \(\\dot{x} = v_0\) a obecnou počáteční výchylku \(x = x_0\) zjistíme:

\[ x(t) = e^{-\zeta \omega_0 t}\left(x_0 \cos{\omega_d t} + \frac{\zeta \omega_n x_0 + v_0}{\omega_d} \sin{\omega_d t}\right)\]

# Define the System Parameters
m = 1.0                   # kg
k = (2.0 * np.pi)**2.     # N/m (Selected to give an undamped natrual frequency of 1Hz)
wn = np.sqrt(k/m)         # Natural Frequency (rad/s)

z = 0.1                   # Define a desired damping ratio
c = 2*z*wn*m              # calculate the damping coeff. to create it (N/(m/s))

wd = wn*np.sqrt(1 - z**2) # Damped natural frequency (rad/s)
# Set up simulation parameters
t = np.linspace(0, 5, 501)          # Time for simulation, 0-5s with 501 points in-between

# Define the initial conditions x(0) = 1 and x_dot(0) = 0
x0 = np.array([-1.0, 0.0])
# Define x(t)
x = np.exp(-z*wn*t)*(x0[0]*np.cos(wd*t) + (z*wn*x0[0] + x0[1])/wd * np.sin(wd*t))
# # Make the figure pretty, then plot the results
# #   "pretty" parameters selected based on pdf output, not screen output
# #   Many of these setting could also be made default by the .matplotlibrc file

# Set the plot size - 3x2 aspect ratio is best
fig = plt.figure(figsize=(6, 4))
ax = plt.gca()
plt.subplots_adjust(bottom=0.17, left=0.17, top=0.96, right=0.96)

# Change the axis units to serif
plt.setp(ax.get_ymajorticklabels(),family='serif',fontsize=18)
plt.setp(ax.get_xmajorticklabels(),family='serif',fontsize=18)

ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# Turn on the plot grid and set appropriate linestyle and color
ax.grid(True,linestyle=':',color='0.75')
ax.set_axisbelow(True)

# Define the X and Y axis labels
plt.xlabel('Čas (s)', family='serif', fontsize=22, weight='bold', labelpad=5)
plt.ylabel('Poloha', family='serif', fontsize=22, weight='bold', labelpad=10)


amp = np.sqrt(x0[0]**2 + ((z*wn*x0[0] + x0[1])/wd)**2)
decay_env = amp * np.exp(-z*wn*t)

# plot the decay envelope
plt.plot(t, decay_env, linewidth=1.0, linestyle = '--', color = "red")
plt.plot(t, -decay_env, linewidth=1.0, linestyle = '--', color = "red")

plt.plot(t, x, linewidth=2, linestyle = '-', label=r'Response')

# uncomment below and set limits if needed
# xlim(0,5)
# ylim(0,10)

plt.yticks([-1.5, -1, -0.5, 0, 0.5, 1, 1.5], ['', r'$-x_0$', '', '0', '', r'$x_0$', ''])

plt.annotate('Exponenciální obálka',
         xy=(t[int(len(t)/3)],decay_env[int(len(t)/3)]), xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=18,
         arrowprops=dict(arrowstyle="simple, head_width = 0.35, tail_width=0.05", connectionstyle="arc3, rad=.2", color="#377eb8"), color = "#377eb8")


# # Create the legend, then fix the fontsize
# leg = plt.legend(loc='upper right', fancybox=True)
# ltext  = leg.get_texts()
# plt.setp(ltext,family='serif',fontsize=18)

# Adjust the page layout filling the page using the new tight_layout command
plt.tight_layout(pad = 0.5)

# save the figure as a high-res pdf in the current folder
# It's saved at the original 6x4 size
# plt.savefig('MCHE485_FreeVibrationWithDamping.pdf')

fig.set_size_inches(9, 6) # Resize the figure for better display in the notebook