Kmitání

import numpy as np
from matplotlib import pyplot as plt

Periodický pohyb a jeho charakteristiky

Periodický pohyb je druh pohybu, při kterém se těleso nebo systém vrací do stejného stavu po určité časové periodě.

Doba potřebná pro jedno úplné opakování pohybu se nazývá perioda a obvykle se označuje písmenem \(T\). Symbol \(P\) se nepoužívá, protože by mohl být zaměněn za hybnost. Jedno úplné opakování pohybu se nazývá cyklus. Jednotkou periody v SI soustavě je sekunda (s).

Matematicky lze periodický pohyb popsat funkcí:

\[x(t+T)=x(t)\]

kde kde \(x(t)\) představuje polohu popisující pohyb v čase \(t\)

Frekvence

Frekvence je definována jako počet cyklů za jednotku času.

Obvykle se značí latinským písmenem \(f\) nebo řeckým písmenem \(\nu\) (ni). Perioda a frekvence jsou vzájemně reciproční veličiny:

\[ f = \frac{1}{T} \]

Například pokud srdce novorozence bije s frekvencí 120 úderů za minutu, pak jeho perioda (čas mezi dvěma údery) je 0,5 sekundy. Obecně platí, že vyšší frekvence odpovídá kratší periodě a naopak.

V SI soustavě je jednotkou frekvence hertz (Hz), pojmenovaný po německém fyzikovi Heinrichu Hertzovi. 1 Hz znamená, že se daná událost opakuje jednou za sekundu.

U rotačních zařízení se často používá tradiční jednotka otáčky za minutu (RPM):

\[ 60 \text{ RPM} = 1 \text{ Hz} \]

Harmonický periodický pohyb

Harmonický periodický pohyb je zvláštní typ periodického pohybu, při kterém je možné popsat polohu tělesa v čase podle sinusové nebo kosinusové funkce.

\[x(t) = A \cos \left(\omega t + \varphi_0 \right)\]

kde

• \(x(t)\) je okamžitá poloha oscilujícího tělesa

• \(t\) je čas

• \(A\) je amplituda – maximální výchylka z rovnovážné polohy,

• \(\omega,\varphi_0\) jsou konstanty popisující pohyb

Úhlová frekvence

Periodický pohyb se často lépe popisuje pomocí úhlové frekvence, která se značí řeckým písmenem \(\omega\) (omega). Úhlová frekvence představuje úhlový posun za jednotku času (například při rotaci) nebo rychlost změny fáze sinusového signálu.

\[ y(t) = \sin(\varphi(t)) = \cos(\omega t) = \cos(2\pi f t) \]

Vzorec pro úhlovou frekvenci:

\[ \omega = 2\pi f \quad \]

Úhlová frekvence se obvykle vyjadřuje v jednotkách radián za sekundu (rad/s), přičemž jeden plný kruh obsahuje 2 \(\pi\) radiánů.

Fáze harmonického pohybu

Fáze harmonického pohybu určuje okamžitý stav oscilátoru v daném čase ( t ). Vyjadřuje se jako argument trigonometrické funkce v rovnici harmonického pohybu:

\[ \varphi(t) = \omega t + \varphi_0 \]

kde:

• \(\varphi(t)\) je okamžitá fáze oscilátoru,

• \(\omega\) je úhlová frekvence,

• \(t\) je čas,

• \(\varphi_0\) je počáteční fáze, která určuje stav oscilátoru v čase \(t = 0\).

Fáze harmonického pohybu určuje, v jaké části cyklu se oscilátor nachází.

• Pokud \(\varphi_0 = 0\), oscilátor začíná v maximální výchylce (při pohybu podle kosinové funkce).

• Pokud \(\varphi_0 = \frac{\pi}{2}\), oscilátor začíná v rovnovážné poloze a pohybuje se směrem nahoru.

Harmonický pohyb lze vyjádřit jako:

\[ x(t) = A \cos(\omega t + \varphi_0) \]

Fáze \(\varphi(t) = \omega t + \varphi_0\) se lineárně zvětšuje v čase, což odpovídá periodicitě pohybu. Fáze se měří v radiánech nebo stupních:

• Pokud fáze dosáhne hodnoty \(2\pi\), oscilátor dokončil jeden úplný cyklus.

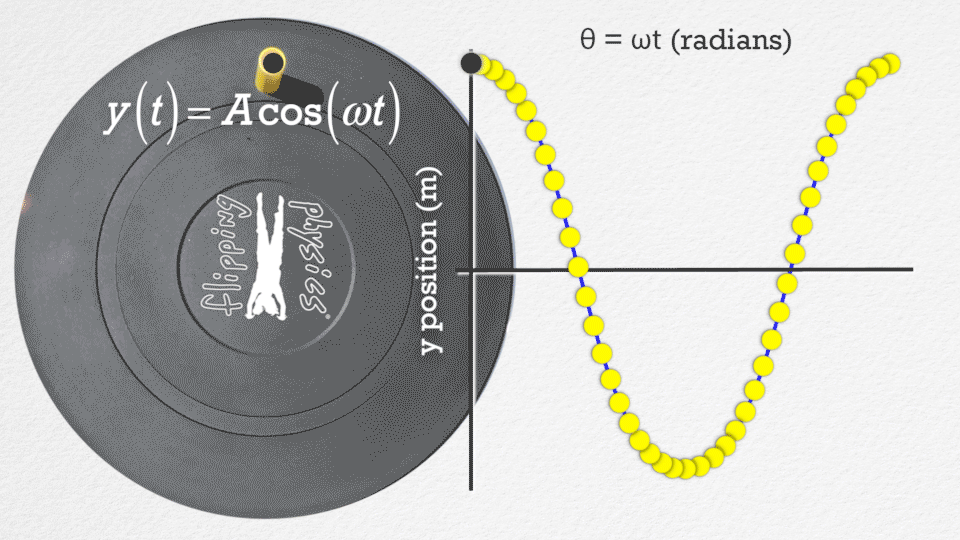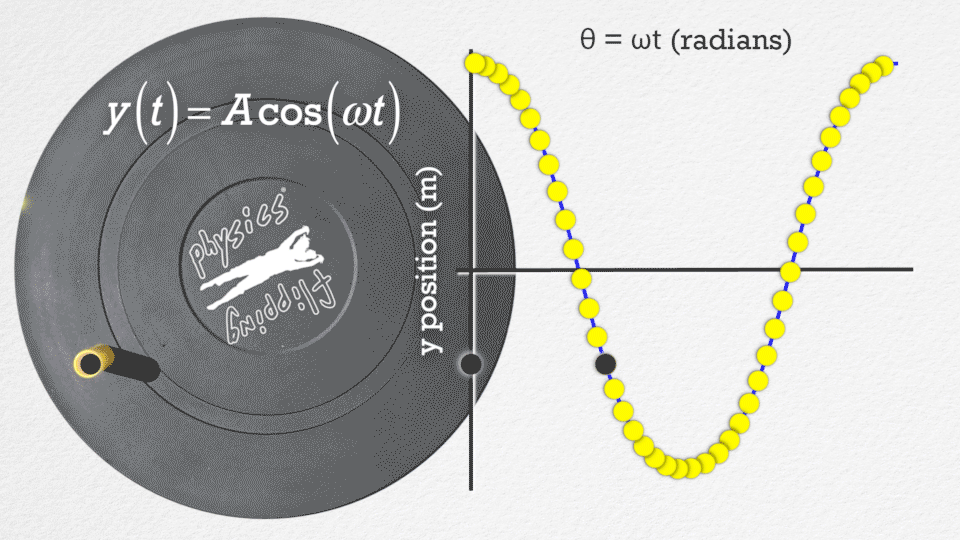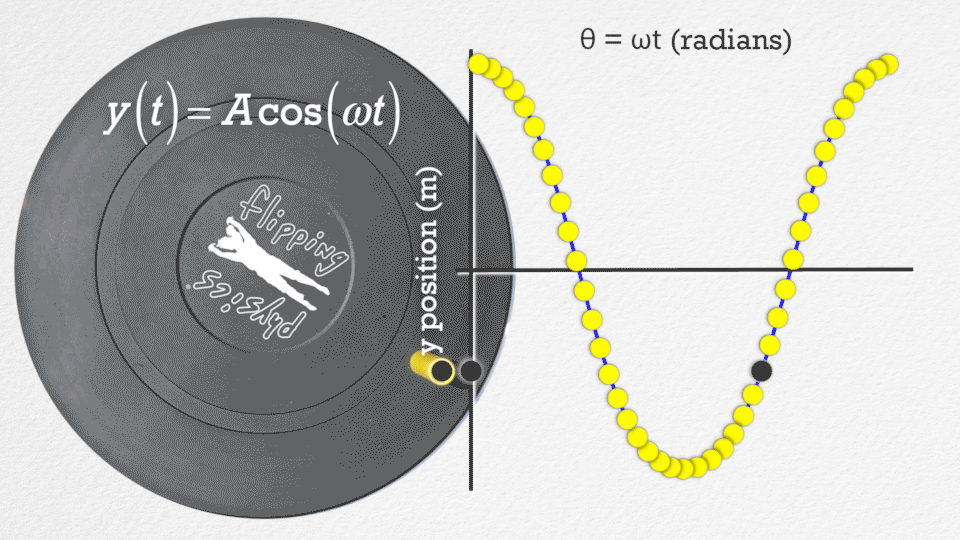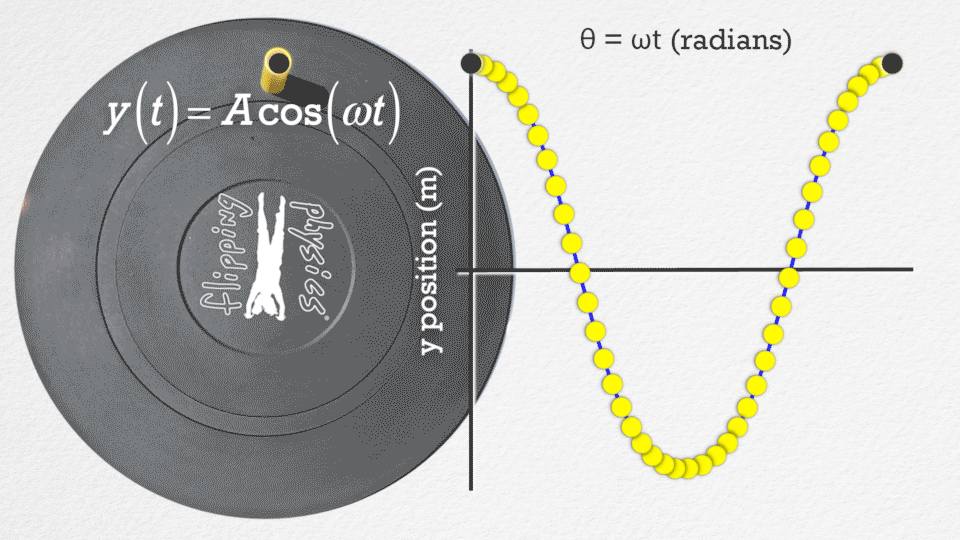
Vztah mezi harmonickým pohybem a pohybem po kružnici

Harmonický pohyb lze chápat jako projekci pohybu po kružnici do jednoho z jeho souřadných směrů. Představme si hmotný bod, který se pohybuje rovnoměrně po kružnici s úhlovou rychlostí \(\omega\). Jeho polohu můžeme popsat pomocí parametrických rovnic:

\[ x(t) = R \cos(\omega t + \varphi_0) \]

\[ y(t) = R \sin(\omega t + \varphi_0) \]

Pokud budeme sledovat pouze souřadnici \(x(t)\), vidíme, že se chová jako harmonický oscilátor s amplitudou \(A = R\).

Rychlost harmonického oscilátoru

Rychlost je první časová derivace polohy:

\[ v(t) = \dot{x} = \frac{dx(t)}{dt} = - A \omega \sin(\omega t + \varphi_0) \]

• Amplituda rychlosti je \(v_{\max} = A \omega\).

• Rychlost je fázově posunuta o \(\frac{\pi}{2}\) oproti poloze – když je výchylka maximální, rychlost je nulová.

• Znaménko rychlosti závisí na směru pohybu:

  • Při pohybu k rovnovážné poloze je rychlost kladná nebo záporná dle směru.

  • Při pohybu od rovnovážné polohy má opačné znaménko.

Zrychlení harmonického oscilátoru

Zrychlení je první derivace rychlosti, tedy druhá derivace polohy:

\[ a(t) = \ddot{x} = \frac{dv(t)}{dt} = - A \omega^2 \cos(\omega t + \varphi_0) \]

• Amplituda zrychlení je \(a_{\max} = A \omega^2\).

• Zrychlení je fázově posunuto o \(\pi\) oproti poloze – vždy směřuje k rovnovážné poloze.

• Znaménko zrychlení:

  • Je kladné, když je výchylka záporná \(x < 0\) – směřuje zpět k rovnovážné poloze.

  • Je záporné, když je výchylka kladná \(x > 0\) – opět směřuje zpět k rovnovážné poloze.

Pojmy kinematiky periodického pohybu

Veličina	Označení	Jednotka (SI)	Popis
Perioda	\(T\)	sekunda (s)	Čas potřebný pro jeden cyklus pohybu.
Frekvence	\(f\) nebo \(\nu\)	hertz (Hz)	Počet cyklů za sekundu. Vztahuje se k periodě jako \(f = \frac{1}{T}\).
Úhlová frekvence	\(\omega\)	rad/s	Udává rychlost změny fáze oscilátoru: \(\omega = 2\pi f\).
Amplituda	\(A\)	metr (m)	Maximální výchylka z rovnovážné polohy.
Fáze	\(\varphi(t)\)	radián (rad)	Okamžitý stav oscilátoru: \(\varphi(t) = \omega t + \varphi_0\).
Počáteční fáze	\(\varphi_0\)	radián (rad)	Fázový posun při \(t = 0\).