Kinematika v 1DOF prostoru

Kinematika v 1DOF prostoru#

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import IFrame

Poloha v 1D#

1D prostor, neboli jednorozměrný prostor, je koncept, který se používá k popisu objektů nebo jevů, které mají pouze jednu dimenzi. Představte si přímku: ta je nekonečně dlouhá, ale nemá žádnou šířku ani hloubku. Vše, co se v 1D prostoru nachází, se dá popsat pouze pomocí jedné souřadnice.

Za 1D prostor můžeme považovat také prostor, kdy pro popsání polohý nám stačí jedna souřadnice. I když se auto pohybuje v 3D prostoru, pro popsání jeho polohy na dálnici nám stačí pouze jedna souřadnice – vzdálenost od počátečního bodu dálnice. Poloha je omezena na jednu dimenzi, i když se odehrává v prostoru s vyšší dimenzí.

Warning

V případě obecného křivočarého pohybu vznikají neinerciální zrychlení a síly, např dostředivé zrychlení při pohybu po kružnici.

Jak si představit 1D prostor

Přímka: Nejjednodušší způsob, jak si představit 1D prostor, je jako přímku. Každý bod na této přímce je určen pouze jednou souřadnicí, která udává jeho vzdálenost od počátku.
Časová osa: Časová osa je také příkladem 1D prostoru. Události se odehrávají v čase a dají se popsat pouze jednou souřadnicí – časem.
Struna: Vibrující struna je fyzikální příklad 1D prostoru. Pohyb bodů na struně se dá popsat pouze jednou souřadnicí – vzdáleností od jednoho konce struny.

Matematický popis 1D prostoru

1D prostor se matematicky popisuje pomocí:

Reálných čísel: Každý bod v 1D prostoru je reprezentován reálným číslem.
Souřadnicové osy: 1D prostor má pouze jednu souřadnicovou osu, obvykle označenou jako osa x.
Vzdálenosti: Vzdálenost mezi dvěma body v 1D prostoru se vypočítá jako absolutní hodnota rozdílu jejich souřadnic.

Pohyb v 1D#

Pro další popis budeme vycházet z definice pohybu. Samotnou změnu fyzikální veličiny označujeme v mechanice symbolem \(\Delta\). Například pro změnu času označíme jako \(\Delta t\). Znamená to:

\[\Delta t = t_2 - t_1\]

Začneme-li pohyb v čase 12 hodin 20 minut a ukočníme ho v čase 12 hodin 21 minut, trval daný pohyb 1 minutu. S popisem změny polohy je to o něco komplikovanější vzhledem k rozdělení pohybu. Kůli jednoduchosti budeme uvažovat nejjednodušší způsob měření pohybu u pohybu posuvného. Pohyb po kružnici si probereme samostatně v části periodického pohybu.

Translační pohyb#

Za nejjednodušší posuvný pohyb budeme považovat pohyb běžce po přímé dráze. Jakým způsobem by jsme mohli určit jeho polohu? Příkladem může být původní měření běhu.

Běh pohyb

Souřadnicová osa#

Počátek souřadnic: Zvolený bod na přímce, od kterého měříme vzdálenosti.
Kladný směr: Směr, ve kterém rostou kladné hodnoty souřadnice.
Záporný směr: Směr opačný ke kladnému směru.

souřadnicová osa

Poloha bodu#

Souřadnice: Číselná hodnota udávající vzdálenost bodu od počátku souřadnic ve zvoleném směru. V případě pohybu po přímce nám stačí jedna hodnota \(x\).

Změna polohy#

Posunutí: Změna polohy bodu v čase. Je to vektorová veličina, která má velikost (dráhu) a směr. Označujeme jí \(\vec{\mathbf{d}}\).

Zápis pohybu#

Možný zápis pohybu je tabulkou, kde vyjádříme jednotlivé body

Čas \(t\) [s]	Poloha \(x\) [m]
0	1
1	3
2	5
3	5
4	2

Zobrazení pomocí tabulky může být nepřehledné když máme velké množství bodů. Proto je výhodnější po popis polohy použít graf. Při spojení jednotlivých naměřených bodů vždy pohyb aproximujeme.

t = [0,1,2,3,4]
x = [1,3,5,5,2]

plt.plot(t,x, "o", label="Naměřené hodnoty")
plt.plot(t,x, "--", label="Aproximace pohybu")
plt.xlabel("Čas [s]")
plt.ylabel("Poloha [m]")
plt.legend()
plt.show()

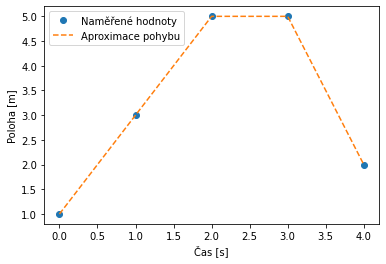
../_images/ada86577407f7ab14e062334eaa8f47b7422139ff5751b10ef8d8e9566923e85.png

Warning

V případě malého počtu naměřených bodů nebo jejich malé frekvence měření vůči pohybu je aproximace pohybu nepřesná.

Kinematika#

Kinematika je odvětví klasické mechaniky, které popisuje pohyb objektů bez uvážení příčin pohybu (Wikipedia).

Kinematika částice je popis pohybu, když je objekt považován za částici.

Částice jako fyzický objekt v přírodě neexistuje; je to zjednodušení pro pochopení pohybu tělesa nebo je to pojmová definice, jako je těžiště soustavy objektů.

Dráha, rychlost a zrychlení jsou tři základní veličiny popisující pohyb tělesa. Mezi nimi existují úzké vztahy, které nám umožňují popsat a analyzovat pohyb tělesa.

Dráha#

Dráha je délka trajektorie, kterou urazí těleso při svém pohybu. Je to skalární veličina a značí se obvykle písmenem s.

Rychlost#

Průměrná rychlost mezi dvěma okamžiky je:

\[\overrightarrow{\mathbf{v_x}}(t) = \frac{\overrightarrow{\mathbf{x}}(t_2)-\overrightarrow{\mathbf{x}}(t_1)}{t_2-t_1} = \frac{\Delta \overrightarrow{\mathbf{x}}}{\Delta t}\]

Okamžitá rychlost částice se získá, když se \(\Delta t\) přiblíží k nule.

\[\overrightarrow{\mathbf{v_x}}(t) = \lim_{\Delta t \to 0} \frac{\Delta \overrightarrow{\mathbf{x}}}{\Delta t} = \lim_{\Delta t \to 0} \frac{\overrightarrow{\mathbf{x}}(t+\Delta t)-\overrightarrow{\mathbf{r}}(t)}{\Delta t} = \frac{\mathrm{d}\overrightarrow{\mathbf{x}}}{\mathrm{d}t} = \dot{\vec{\mathbf{x}}}\]

Note

V mechanice se často setkáváme s časovými derivacemi, tedy derivacemi funkcí, které závisí na čase. Pro zjednodušení zápisu a usnadnění práce s těmito derivacemi se používá speciální značení pomocí teček nad symbolem veličiny. Toto značení zavedl Isaac Newton.

První časová derivace: Značí se jednou tečkou nad symbolem veličiny. Například, pokud \(x\) značí polohu, pak \(\dot{x}\) (x s tečkou) značí její první časovou derivaci, tedy rychlost:

\[\dot{x} = \frac{dx}{dt}\]
Druhá časová derivace: Značí se dvěma tečkami nad symbolem veličiny. Například, \(\ddot{x}\) (x se dvěma tečkami) značí druhou časovou derivaci polohy, tedy zrychlení:

\[\ddot{x} = \frac{d^2x}{dt^2} = \frac{d}{dt}\left(\frac{dx}{dt}\right) = \frac{d\dot{x}}{dt}\]

Třetí a vyšší časové derivace: Značí se třemi a více tečkami nad symbolem veličiny. Vyšší časové derivace se používají méně často, ale mohou se objevit například při popisu dynamiky pohybu.

Rychlost je relativní#

Rychlost je vždy relativní. To znamená, že se udává vzhledem k nějakému referenčnímu bodu nebo soustavě. Neexistuje absolutní rychlost. Pojďme si to ilustrovat na několika příkladech s ohledem na Zemi, Slunce a centrum naší Galaxie, Mléčné dráhy.

1. Vzhledem k Zemi:

Chůze: Člověk jde rychlostí například 5 km/h. Tato rychlost je vzhledem k povrchu Země.
Auto: Auto jede rychlostí 100 km/h. Opět, tato rychlost je vzhledem k Zemi.
Letadlo: Letadlo letí rychlostí 900 km/h. Tato rychlost je vzhledem k Zemi.

V těchto příkladech je Země naše nejpřirozenější referenční soustava. Všichni se pohybujeme po Zemi a proto nám tyto rychlosti dávají největší smysl.

2. Vzhledem ke Slunci:

Země obíhá kolem Slunce. To znamená, že i když stojíme na Zemi, pohybujeme se obrovskou rychlostí vzhledem ke Slunci.

Rychlost Země kolem Slunce: Přibližně 30 km/s (108 000 km/h). To je mnohem rychleji, než cokoliv, co běžně zažíváme na Zemi. I když sedíte v klidu doma, pohybujete se touto obrovskou rychlostí vzhledem ke Slunci.
Rychlost sondy Voyager 1 (vzhledem ke Slunci): Voyager 1, jedna z nejvzdálenějších sond od Země, se pohybuje rychlostí přibližně 17 km/s (61 200 km/h) vzhledem ke Slunci.

Zde vidíme, že i relativně “pomalu” se pohybující tělesa (jako Země) mají obrovské rychlosti, pokud změníme referenční soustavu na Slunce.

3. Vzhledem k centru Galaxie:

Slunce a celá Sluneční soustava obíhají kolem centra Mléčné dráhy. I zde se pohybujeme obrovskou rychlostí.

Rychlost Slunce kolem centra Galaxie: Přibližně 220 km/s (828 000 km/h). To je ještě mnohem rychlejší než pohyb Země kolem Slunce! I Slunce, obrovská a zdánlivě nehybná hvězda, se řítí vesmírem obrovskou rychlostí vzhledem k centru Galaxie.

Zde je Země pouze malou planetou obíhající kolem Slunce, které je jednou z miliard hvězd obíhajících centrum Galaxie. Proto se naše rychlost vzhledem k centru Galaxie skládá z rychlosti Země kolem Slunce a rychlosti Slunce kolem centra Galaxie.

Shrnutí:

Vzhledem k	Příklad	Rychlost (přibližně)
Zemi	Chůze	5 km/h
Rovník	Osa otáčení Země	1674 km/h
Slunci	Země	108 000 km/h)
Centru Galaxie	Slunce	828 000 km/h)
Mléčna dráha	ostatní galaxie	2.2 miliona km/h
Zdroj: Britannica.com

Zrychlení#

Zrychlení je změna rychlosti bodu, která může být dána i rychlostí změny polohy druhého řádu. Střední zrychlení mezi dvěma okamžiky je:

\[\overrightarrow{\mathbf{a}}(t) = \frac{\overrightarrow{\mathbf{v}}(t_2)-\overrightarrow{\mathbf{v}}(t_1)}{t_2-t_1} = \frac{\Delta \overrightarrow{\mathbf{v}}}{\Delta t}\]

Podobně okamžité zrychlení je derivace prvního řádu rychlosti nebo derivace druhého řádu polohového vektoru:

\[\overrightarrow{\mathbf{a}}(t) = \frac{\mathrm{d}\overrightarrow{\mathbf{v}}(t)}{\mathrm{d}t} = \frac{\mathrm{d}^2\overrightarrow{\mathbf{x}}(t)}{\mathrm{d}t^2} = \dot{\vec{\mathbf{v}}} =\ddot{\vec{\mathbf{x}}}\]

Ryv (Jerk)#

Ryv (anglicky jerk) je fyzikální veličina, která popisuje změnu zrychlení v čase. Udává, jak rychle se zrychlení tělesa mění. Je to vektorová veličina, což znamená, že má velikost a směr.

Ryv se značí písmenem \(j\) a jeho definiční vztah je dán derivací zrychlení (\(a\)) podle času (\(t\)):

\[ \vec{\mathbf{j}} = \frac{\mathrm{d}\vec{\mathbf{a}}}{\mathrm{d}t} = \frac{\mathrm{d}^3\mathbf{x}}{\mathrm{d}t^3} \]

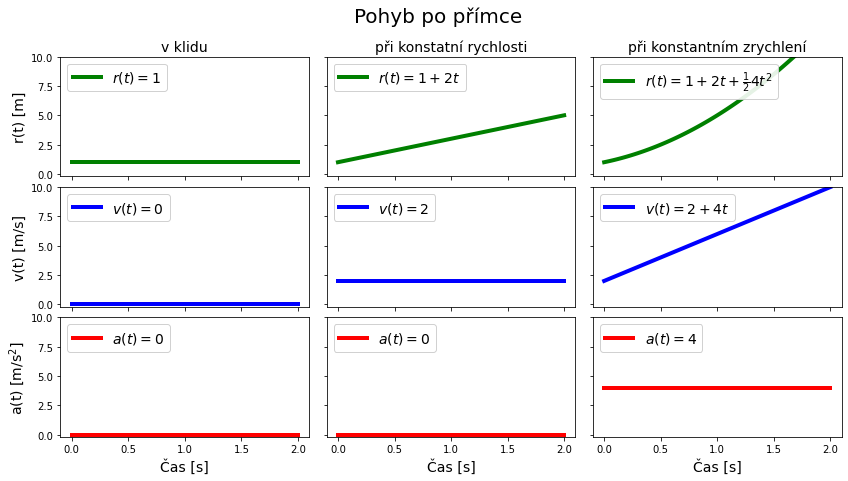
Příklady pohybu v 1D#

Bod při konstantní rychlosti#

\[\begin{split} \begin{array}{l l} \overrightarrow{\mathbf{a}}(t) = 0 \\ \overrightarrow{\mathbf{v}}(t) = \overrightarrow{\mathbf{v}}_0 \\ \overrightarrow{\mathbf{r}}(t) = \overrightarrow{\mathbf{r}}_0 + \overrightarrow{\mathbf{v}}_0t \end{array} \end{split}\]

Bod při konstantním zrychlení#

\[\begin{split} \begin{array}{l l} \overrightarrow{\mathbf{a}}(t) = \overrightarrow{\mathbf{a}}_0 \\ \overrightarrow{\mathbf{v}}(t) = \overrightarrow{\mathbf{v}}_0 + \overrightarrow{\mathbf{a}}_0t \\ \overrightarrow{\mathbf{r}}(t) = \overrightarrow{\mathbf{r}}_0 + \overrightarrow{\mathbf{v}}_0t + \frac{1}{2}\overrightarrow{\mathbf{a}}_0 t^2 \end{array} \end{split}\]

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t = np.linspace(0, 2, 101)
r0 = 1
v0 = 2
a0 = 4

plt.rc('axes',  labelsize=14,  titlesize=14) 
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10) 
f, axarr = plt.subplots(3, 3, sharex = True, sharey = True, figsize=(14,7))
plt.suptitle('Pohyb po přímce', fontsize=20);

tones = np.ones(np.size(t))

axarr[0, 0].set_title('v klidu', fontsize=14);
axarr[0, 0].plot(t, r0*tones, 'g', linewidth=4, label='$r(t)=1$')
axarr[1, 0].plot(t,  0*tones, 'b', linewidth=4, label='$v(t)=0$')
axarr[2, 0].plot(t,  0*tones, 'r', linewidth=4, label='$a(t)=0$')
axarr[0, 0].set_ylabel('r(t) [m]')
axarr[1, 0].set_ylabel('v(t) [m/s]')
axarr[2, 0].set_ylabel('a(t) [m/s$^2$]')

axarr[0, 1].set_title('při konstatní rychlosti');
axarr[0, 1].plot(t, r0*tones+v0*t, 'g', linewidth=4, label='$r(t)=1+2t$')
axarr[1, 1].plot(t, v0*tones,      'b', linewidth=4, label='$v(t)=2$')
axarr[2, 1].plot(t,  0*tones,      'r', linewidth=4, label='$a(t)=0$')

axarr[0, 2].set_title('při konstantním zrychlení');
axarr[0, 2].plot(t, r0*tones+v0*t+1/2.*a0*t**2,'g', linewidth=4,
                 label='$r(t)=1+2t+\\frac{1}{2}4t^2$')
axarr[1, 2].plot(t, v0*tones+a0*t,             'b', linewidth=4,
                 label='$v(t)=2+4t$')
axarr[2, 2].plot(t, a0*tones,                  'r', linewidth=4,
                 label='$a(t)=4$')

for i in range(3): 
    axarr[2, i].set_xlabel('Čas [s]');
    for j in range(3):
        axarr[i,j].set_ylim((-.2, 10))
        axarr[i,j].legend(loc = 'upper left', frameon=True, framealpha = 0.9, fontsize=14)
        
plt.subplots_adjust(hspace=0.09, wspace=0.07)

../_images/dc639cc5f376c8ff27e1b948d78c3c185360759f261b69ec78fbc7351bded44c.png

Kinematika závodu na 100 m#

Příkladem, kde lze analýzu některých aspektů pohybu lidského těla zredukovat na analýzu bodu, je studium biomechaniky běhu na 100 metrů.

Technickou zprávu s kinematickými daty pro světový rekord na 100 m od Usaina Bolta si můžete stáhnout z website for Research Projects od Mezinárodní asociace atletických federací. Tady je přímý odkaz. Konkrétně následující tabulka ukazuje údaje pro tři medailisty v tomto závodě:

částečné časy závodu na 100 metrů v Berlíně 2009 — *Obrázek. Údaje od tří medailistů z běhu na 100 m v Berlíně, 2009 (0print report).*

Sloupec RT v tabulce výše se týká reakční doby každého sportovce. IAAF má velmi přísné pravidlo o reakční době: každý sportovec s reakční dobou kratší než 100 ms je ze soutěže diskvalifikován! Diskuzi o tomto pravidle naleznete na webu Reaction Times and Sprint False Starts.

Svou vlastní reakční dobu si můžete změřit jednoduchým způsobem na této webové stránce: http://www.humanbenchmark.com/tests/reactiontime.

Článek A Kinematics Analysis Of Three Best 100 M Performances Ever od Krzysztofa a Mera představuje podrobnou kinematickou analýzu závodů na 100 m.

Vztah mezi dráhou, rychlostí a zrychlením#

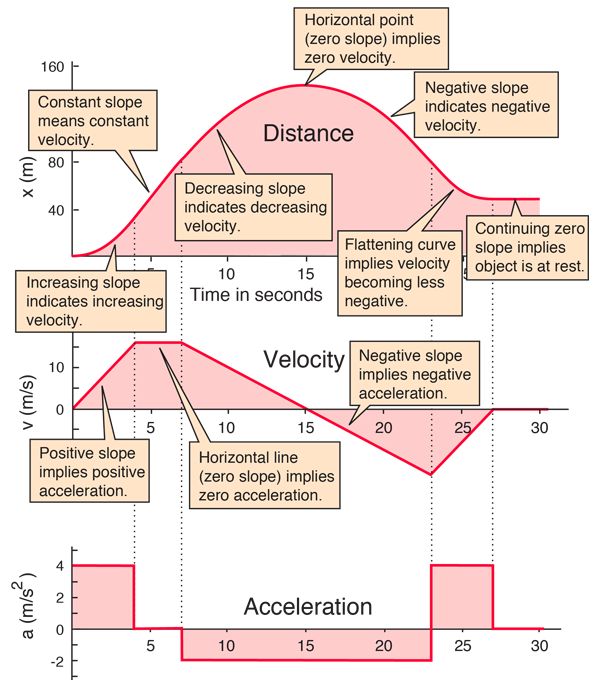
Graf dráhy: Ukazuje, jak se mění poloha tělesa v čase.

Graf rychlosti: Ukazuje, jak se mění rychlost tělesa v čase.

Graf zrychlení: Ukazuje, jak se mění zrychlení tělesa v čase.

Při rovnoměrném přímočarém pohybu: Rychlost je konstantní a dráha je přímo úměrná času, zrychlení je nulové.

Při rovnoměrně zrychleném přímočarém pohybu: Rychlost se lineárně zvětšuje s časem a dráha se mění kvadraticky s časem.