Smykové napětí

import numpy as np
from matplotlib import pyplot as plt

Smykové napětí v rovině

Smykové napětí \(\tau\) popisuje vnitřní síly v materiálu působící rovnoběžně s danou plochou. Je definováno jako síla působící na jednotkovou plochu:

\[ \tau = \frac{F}{A} \]

kde:

• \(F\) je smyková síla působící v rovině,

• \(A\) je plocha, na kterou síla působí.

Smykové napětí způsobuje deformaci, kterou vyjadřujeme pomocí smykové deformace (\(\gamma\)), což je úhel změny mezi původně kolmými přímkami v materiálu.

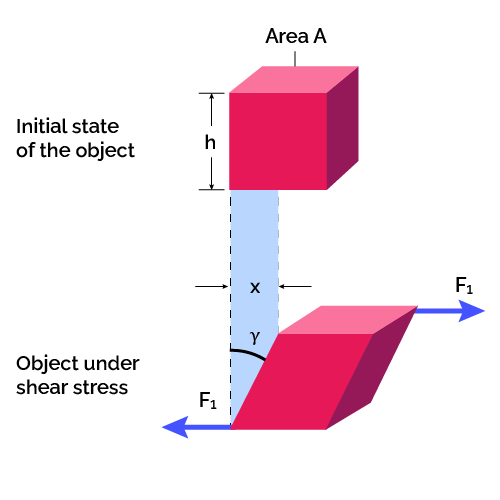
Deformaci ve smyku můžeme vyjádřit také pomocí poměrného napětí

\[\gamma = \frac{\Delta x}{h}\]

Smykové napětí je lineárně úměrné smykové deformaci, což vyjadřuje Hookeův zákon pro smyk:

\[ \tau = G \gamma \]

kde \(G\) je modul pružnosti ve smyku (smykový modul), který charakterizuje odolnost materiálu vůči smykovým deformacím.

Zákon sdružených smykových napětí

Zákon sdružených smykových napětí vyjadřuje, že smyková napětí na dvou navzájem kolmých rovinách jsou si rovna.

Matematicky:

\[ \tau_{xy} = \tau_{yx} \]

Odvození

Uvažujme malý elementární kvádr v rovnováze. Pro smykové síly působící na protilehlé stěny kvádru musí platit rovnováha momentů. Například pro smykové napětí \(\tau_{xy}\) a \(\tau_{yx}\):

• Síla na stěně \(x\) ve směru \(y\) vyvolává moment kolem osy \(z\).

• Stejnou velikost momentu musí vyvolávat síla na stěně \(y\) ve směru \(x\).

• Proto musí platit \(\tau_{xy} = \tau_{yx}\).

Podobný postup lze aplikovat na další smyková napětí.

Vztah mezi modulem pružnosti \(G\) a Youngovým modulem \(E\)

Pro izotropní materiály existuje vztah mezi smykovým modulem \(G\), Youngovým modulem \(E\) a Poissonovým číslem \(\nu\). Vyjdeme z rovnice pro objemovou deformaci v Hookeově zákoně:

\[ G = \frac{E}{2(1+\nu)} \]

Napětí v čistém smyku

Základní vztah mezi napětím a deformací pro izotropní materiály v Hookeově zákoně ve dvourozměrném prostoru je:

\[ \varepsilon_x = \frac{1}{E} \left[ \sigma_x - \nu (\sigma_y) \right] \]

Podobně pro smykové deformace platí:

\[ \gamma_{xy} = \frac{\tau_{xy}}{G} \]

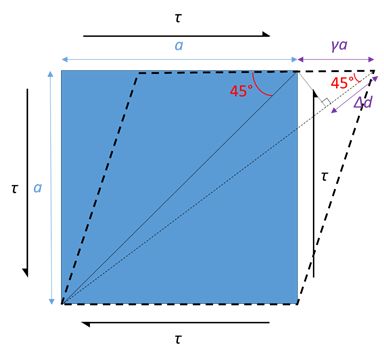
Uvažujme krychli o straně \(a\). Předpokládejme působení smykového napětí \(\tau\), které vyvolá malo deformaci \(\gamma\). Deformace uhlopříčky krychle je

\[\frac{{{\rm{\Delta }}d}}{{\sqrt 2 a}} = \frac{{\gamma a\;{\rm{cos}}45^\circ }}{{\sqrt 2 a}} = \frac{\gamma }{2} \]

Z definice modulu pružnosti ve smyku plyne, že deformace ve směru uhlopříčky je

\[\epsilon_\parallel = \frac{\tau}{2G} \]

Deformace ve směru druhé uhlopříčky je

\[\epsilon_\perp = -\frac{\tau}{2G} \]

Dosazením do Hookova zákona získáme

\[\frac{\tau}{2G} = \frac{1}{E} \left[ \sigma_\parallel - \nu \sigma_\perp \right] \]

\[-\frac{\tau}{2G} = \frac{1}{E} \left[ \sigma_\perp - \nu \sigma_\parallel \right] \]

Z uvedeného plyne, že

\[ \sigma_\perp = - \sigma_\parallel \]

a napětí můžeme vyjádřit ve formě.

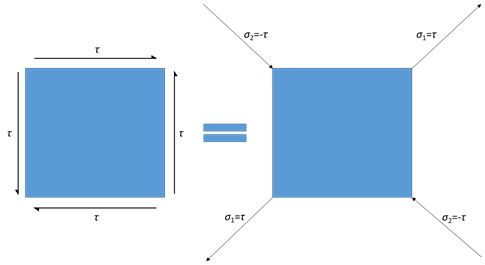
Z Mohrovy kružnice plyne, že při prostém smyku platí

\(\sigma_1 =\sigma_\perp = \tau; \sigma_2 = \sigma_\parallel = -\tau;\)

Proto můžeme napsat

\[\frac{\tau}{2G} = \frac{\tau}{E} (1 + \nu)\]

a

\[ G = \frac{E}{2(1+\nu)} \]

Závěr

• Smykové napětí popisuje síly působící rovnoběžně s povrchem tělesa a je úměrné smykové deformaci.

• Modul pružnosti ve smyku ( G ) je spojen s Youngovým modulem ( E ) a Poissonovým číslem ( \nu ) vztahem:

  \[ G = \frac{E}{2(1+\nu)} \]

• Zákon sdružených smykových napětí říká, že smyková napětí na navzájem kolmých plochách jsou si rovna:

  \[ \tau_{xy} = \tau_{yx}, \quad \tau_{xz} = \tau_{zx}, \quad \tau_{yz} = \tau_{zy} \]

Tento zákon plyne z rovnováhy momentů v elementárním objemu.