Hookeův zákon#
from IPython.display import IFrame
from IPython.display import YouTubeVideo
Přechod od pohybových sil ke změnám tvaru#
Nyní se přesuneme od úvah o silách, které ovlivňují pohyb objektu (například tření a odpor vzduchu), k těm, které ovlivňují tvar objektu. V případě působení velkých sil dojde ke změně tvaru objektu. Například když silně zatlačíme na hřebík, nepohne se z místa ale působící síla změní jeho tvar. Změna tvaru v důsledku působení síly se nazývá deformace.

Zároveň k deformacím dochází také při působení velmi malých sil. Tyto deformace jsou mnohem menší a platí pro ně dvě důležité charakteristiky:
Elasticita – Objekt se po odstranění síly vrátí do svého původního tvaru, tedy deformace je elastická.
Proporcionalita – Velikost deformace je úměrná působící síle, což znamená, že pro malé deformace platí Hookeův zákon.
Note
Hookeův zákon Hookeův zákon je pojmenován po britském fyzikovi Robertu Hookovi ze 17. století a poprvé byl formulován v roce 1676 jako latinská anagramová hádanka “ceiiinosssttuv”. Její řešení Hooke zveřejnil v roce 1678 ve formě věty Ut tensio, sic vis, což znamená “Jaké prodloužení, taková síla.”
Matematicky lze Hookeův zákon vyjádřit jako:
kde:
\(\Delta l\) je velikost deformace (například změna délky),
\(F\) je působící síla,
\(k\) je konstanta úměrnosti závislá na tvaru a materiálu objektu. Tuto konstantu úměrnosti označujeme jako tuhost (stiffness). Tuhost je fyzikální veličina charakterizující odpor tělesa nebo materiálu vůči deformaci při působení síly. Vyjadřuje, jak velká síla je potřebná k vyvolání určité deformace. Jednotkou tuhosti je N/m.
Caution
Elastická síla není konstatní Je důležité si uvědomit, že tato síla působí proti působící vnější síle podobně jako síla tření a závisí na deformaci \(\Delta l\) – není konstantní jako síla tření.
Přepíšeme-li rovnici do tvaru:
je jasné, že deformace je přímo úměrná aplikované síle (Ut tensio, sic vis). Převrácená hodnota tuhosti se označuje jako poddajnost (compliance). Poddajnost je fyzikální veličina vyjadřující schopnost tělesa nebo materiálu podléhat deformaci při působení síly.
kde:
\(C\) je poddajnost [m/N],
\(k\) je tuhost [N/m]).
Vztah mezi deformací \(\Delta l\) a aplikovanou silou \(F\) lze vyjádřit jako:
Tento vztah ale neplatí pro libovolné síly. Na obrázku je graf deformace \(\Delta l\) versus aplikovaná síla \(F\). Přímý úsek představuje lineární oblast, kde platí Hookeův zákon. Sklon tohoto přímého úseku je \(1/k\). Při větších silách se graf zakřivuje, ale deformace je stále elastická—po odstranění síly se \(\Delta l\) vrátí na nulu. Při ještě větších silách dochází k trvalé deformaci objektu, která nakonec vede k jeho zlomu. Všimněte si, že v tomto grafu se těsně před zlomením sklon zvětšuje, což znamená, že malý nárůst síly \(F\) způsobuje výrazné prodloužení \(\Delta l\) v blízkosti zlomu.
IFrame("https://www.geogebra.org/classic/tb98aHHz?embed", width="800", height="600")
Na čem záleží tuhost?#
Caution
Tuhost je vlastnost tělesa Tuhost závisí nejen na materiálových vlastnostech, ale také na geometrii objektu (např. průřezu nebo délce). Proto mají dva objekty ze stejného materiálu různou tuhost, pokud mají odlišné rozměry nebo tvar.
Z Hookeova zákona plyne, že prodloužení \(\Delta l\) je funkcí působící síly. Na čem ale závisí samotná tuhost objektu. Přčdepokládejme, že na gitarové struny působíme stejnou sílou. Stejná síla, v tomto případě tíha \(W\), vede k různé výslední deformaci. Výsledné deformace jsou na obrázku níže znázorněny jako šedé segmenty.

Struna vlevo je tenká nylonová - pozorujeme velkou deformaci.
Struna uprostřed je tlustší nylonová - pozorujeme menší deformaci.
Struna vpravo je ocelová - deformaci téměř nepozorujeme.
Každá struna se deformuje jinak, což ukazuje, že tuhost závisí na:
Materiálu – Ocelová struna má vyšší modul pružnosti než nylonová, a proto se méně deformuje.
Průměru (ploše průřezu) – Tlustší nylonová struna je tužší než tenčí, protože větší průřez zvyšuje odpor vůči deformaci.
Délce – I když v tomto případě jsou všechny struny stejně dlouhé, obecně platí, že delší objekty mají menší tuhost (při stejné síle se více deformují).
V případě, že by jsme zkoušeli struny různé délky, zjistili by jsme, že celkové prodloužení závisí na velikosti původní délky:
Dále by jsme mohli zjistit, že prodloužení je menší u materiálů s větším průřezem
Když tyto závislosti vložíme do Hookeova zákona zjistíme
nebo můžeme přepsat do tvaru
kde:
\(\sigma\) je napětí, [ N/m\(^2\)]
\(\varepsilon\) je poměrné prodloužení, [1]
\(E\) je Youngův modul pružnosti, [Pa]
Hookův zákon v tomto tvaru bývá také označován jako elementární Hookův zákon a můžeme ho formulovat:
Normálové napětí je přímo úměrné relativnímu prodloužení.
\[ \sigma = E \varepsilon \]
Napětí (stress)#
Napětí vyjadřuje vnitřní sílu působící v materiálu v důsledku vnějšího zatížení. Udává, jak velká síla působí na jednotkovou plochu průřezu.
Matematicky je definováno vztahem:
kde:
\(\sigma\) je normálové napětí [Pa = N/m^2],
\(F\) je působící síla [N],
\(A\) je plocha průřezu [m\(^2\)].
Napětí může být:
Tahové (\(\sigma > 0\)) – materiál se prodlužuje.
Tlakové (\(\sigma < 0\)) – materiál se zkracuje.
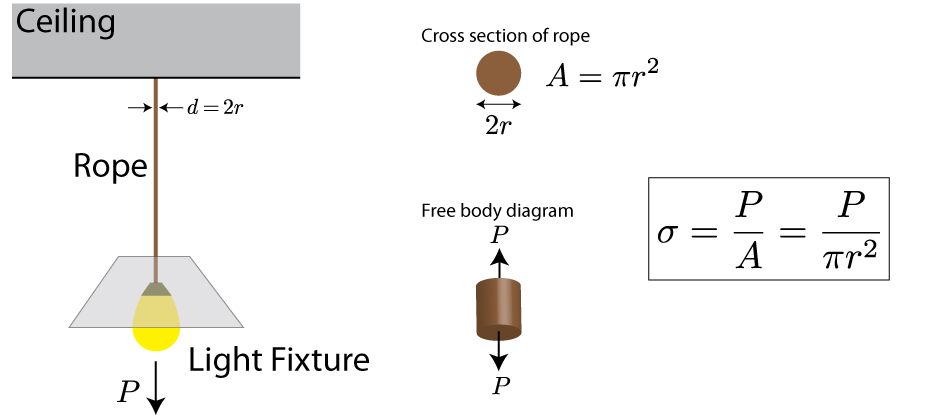
V rámci tohoto kurzu budeme předpokládat, že všechny materiály jsou homogenní, izotropní a elastické. Také budeme uvažovat, že objekt je prizmatický – to znamená, že průřez je po celé délce stejný (například banán je přibližně prizmatický, zatímco jablko není). Tyto předpoklady nám umožňují říci, že objekt se bude deformovat rovnoměrně v každém bodě svého průřezu a napětí je konstatní.
V případě, že napětí v průřezu není konstatní přenáší malá plocha průřezu \(\Delta A\) malou sílu \(\Delta F\) a můžeme definovat napětí v bodě, když dané plochy a síly budeme zmenšovat:
a součet všech těchto sil musí být roven výsledné vnitřní síle \(F\).
Tento vztah vyjadřuje průměrné normálové napětí, protože jsme vnitřní síly zprůměrovali po celém průřezu.
Napětí je často obtížné pochopit, protože není přímo viditelné. Existuje však metoda, která umožňuje vizualizaci napětí – pozorováním průhledného z určitých materiálů objektu v polarizovaném světle. Tento jev je známý jako fotoelasticita.
YouTubeVideo('MhcsqX9u1pU')
Napětí může v materiálu existovat i bez působícího zatížení. Tomu se říká zbytkové napětí, které může být výhodné pro zvýšení pevnosti materiálů – například při výrobě japonských katan. Naopak, nežádoucí zbytková napětí mohou podporovat růst trhlin a vést k porušení materiálu. Příkladem je zhroucení mostu Silver Bridge v Západní Virginii v roce 1967.
Jedním z nejzajímavějších příkladů zbytkového napětí je fenomén rychlého ochlazování roztaveného skla, známý jako Prince Rupert’s Drop.
YouTubeVideo('xe-f4gokRBs')
Poměrné prodloužení (strain)#
Poměrné prodloužení je bezrozměrná veličina, která vyjadřuje relativní změnu délky materiálu při deformaci.
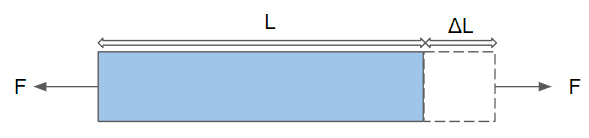
Matematicky se definuje jako:
kde:
\(\varepsilon \) je poměrné prodloužení [-],
\(\Delta l \) je změna délky tělesa [m],
\(l_0 \) je původní délka tělesa [m].
Poměrné prodloužení je kladné při tahu a záporné při tlaku.
Na rozdíl od napětí, je možné deformace přímo vidět a měřit. V elastické oblasti jsou ale běžné deformace malé pro inženýrské materiály, typicky v rozsahu mikrometrů. Pro měření proto využíváme senzor, který se označuje pojmem tenzometr.
Příkladem může být odporový tenzometr, u kterého při deformaci dochází ke změně elektrického odporu, což lze přesně změřit. Tenzometr pracuje na základě závislosti elektrického odporu vodiče na jeho délce a průřezu. Elektrický odpor vodiče je dán vztahem:
kde:
\(R\) je elektrický odpor [\(\Omega\)],
\(\rho\) je měrný elektrický odpor materiálu [\(\Omega\) m],
\(L\) je délka vodiče [m],
\(A\) je plocha průřezu vodiče [m\(^2\)].
Při natažení tenzometru se délka vodiče zvětší a průřez zmenší, což vede k zvýšení odporu. Naopak při stlačení se odpor sníží. Změna odporu \(\Delta R\) je úměrná poměrnému prodloužení podle vztahu:
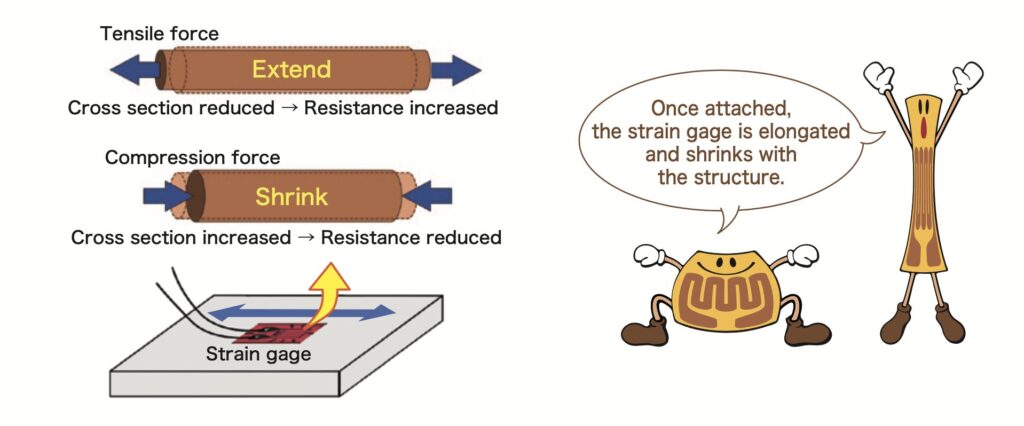
kde:
\(K\) je tenzometrický faktor (typicky kolem 2 pro kovové tenzometry),
\(\varepsilon\) je poměrné prodloužení [1]
Youngův modul pružnosti (modul pružnosti v tahu)#
Youngův modul pružnosti ( E ) charakterizuje schopnost materiálu odolávat deformaci při působení napětí.
Youngův modul pružnosti definován jako poměr normálového napětí k odpovídající poměrné deformaci v oblasti lineární pružnosti materiálu:
kde:
\(E\) je Youngův modul pružnosti (Pa, N/m²)
\(\sigma\) je normálové napětí (Pa, N/m²)
\(\varepsilon\) je poměrná deformace (bezrozměrná veličina)
V diagramu napětí–deformace odpovídá Youngův modul pružnosti směru (sklonu) přímé části křivky, tedy oblasti, kde platí Hookeův zákon. Čím strmější je tato část křivky, tím je materiál tuhší a odolnější vůči deformaci.

Při stejném napětí v tahu prokazuje materiál „B“ podstatně větší deformaci než materiál „A“. Materiál „A“ má tedy větší modul pružnosti v tahu než materiál „B“. Vyšší hodnota modulu pružnosti znamená, že materiál je tuhší a méně se deformuje při stejném zatížení.
Note
Thomas Young (1773–1829) Thomas Young byl britský fyzik, lékař a polyhistor, kterému říkali The Last Man Who Knew Everything. Popsal akomodaci oka a roli čočky při ostření obrazu a je pokládám za zakladatele fyziologie oka. Proslavil se také svým dvojštěrbinovým experimentem, který poskytl důkaz o vlnové povaze světla. Podílel se na rozluštění egyptských hieroglyfů.
Young popsal charakterizaci pružnosti, která se stala známou jako Youngův modul, označovaný jako \(E\), v roce 1807 a dále ji rozvinul ve svém díle Course of Lectures on Natural Philosophy and the Mechanical Arts. Nicméně první experimentální použití konceptu Youngova modulu provedl Giordano Riccati již v roce 1782, tedy o 25 let dříve než Young. Navíc lze tuto myšlenku vystopovat až k článku Leonarda Eulera, publikovanému v roce 1727, tedy přibližně 80 let před Youngovým článkem z roku 1807.

