Analýza dat z tahového diagramu

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from lmfit import Model
%matplotlib inline

Dva datové soubory .xls obsahující data z tahové zkoušky jsme získali z věřejně přístupných zdrojů. Popisují naměřená data při zkoušce oceli 1045 slitiny hliníku 6061.

Načtení dat z Excelu

Nejdříve si pomocí funkce %ls ověříme, že nás adresář obsahuje data z měření. Tato funkce nám vypíše obsah adresáře.

Pomocí funkce pd.read_excel() z balíčku pandas je možné přímo načíst data. Data ze dvou excelových souborů budou uložena ve dvou datových objektech nazvaných steel_df a al_df. Datový objekt pandas je tabulkový datový typ.

K zobrazení prvních pěti řádků každého datového rámce můžeme použít metodu .head().

%ls ../data/ 
df_al = pd.read_excel('../data/Al60601_raw_data.xls')
df_al.head()

Al60601_raw_data.xls  Steel1018_raw_data.xls

WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero

	TESTNUM	POINTNUM	TIME	POSIT	FORCE	EXT	CH5	CH6	CH7	CH8
0	542	1	8.470	0.02256	201.146011	-0.001444	0.007552	NaN	NaN	NaN
1	542	2	8.632	0.02330	206.599442	0.000302	0.007552	NaN	NaN	NaN
2	542	3	10.027	0.02846	287.512573	0.003044	0.018898	NaN	NaN	NaN
3	542	4	11.031	0.03232	365.380981	0.009881	0.022061	NaN	NaN	NaN
4	542	5	11.928	0.03616	447.813965	0.014085	0.033652	NaN	NaN	NaN

df_steel = pd.read_excel('../data/Steel1018_raw_data.xls')
df_steel.head()

WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero

	TESTNUM	POINTNUM	TIME	POSIT	FORCE	EXT	CH5	CH6	CH7	CH8
0	523	1	6.189	0.07302	202.924728	0.000402	-0.028272	NaN	NaN	NaN
1	523	2	6.549	0.07396	205.714890	-0.000238	-0.034549	NaN	NaN	NaN
2	523	3	7.148	0.07624	217.763336	-0.000713	-0.030140	NaN	NaN	NaN
3	523	4	9.146	0.08438	316.306122	0.002377	-0.025968	NaN	NaN	NaN
4	523	5	10.041	0.08822	417.003357	0.003089	-0.024100	NaN	NaN	NaN

Vidíme, že naměřená data obashují různé hodnoty. Pro nás je nejdůležitejší sloupec síla (FORCE). Kromě těchto hodnot máme k dispozici ještě hodnotu EXT hodnoty prodloužení z mechanického extenzometeru v % a CH5, který obsahuje hodnoty prodloužení z laserového extensometru v %.

Úprava dat

Protože tato data jsme získali z americké laboratoře, máme sílu určenou v librách (pounds) a průmer zkušební tyče je 0.506 palců (inch). Nejdříve musíme tyto hodnoty převést na jednotky SI.

• Pro převod síly nebo hmotnosti z liber (lb) na newtony (N) použijeme následující vztah: 1 lb \(\approx\) 4,4822162 N.

• Pro převod délky z palců (inch) na milimetry (mm) použijeme následující vztah: 1 inch = 25.4 mm.

Note

Síla v N, rozměry v mm, napětí v MPa $\(1 \frac{\mathrm{N}}{\mathrm{mm}^2} = 1\,10^6 \frac{\mathrm{N}}{\mathrm{m}^2} = 1 \mathrm{MPa}\)$

d = 0.506 * 25.4 # mm
force_al = df_al['FORCE'].to_numpy() *  4.4822162#N
force_steel = df_steel['FORCE'].to_numpy() * 4.4822162 #N

Následně si určíme smluvné napětí vydělením síly počátečným průřezem a převedem prodloužení z procent. Protože laserový exntezometr je přesnější, budeme počítat s těmito daty.

A = np.pi*d**2/4
stress_al = force_al / A
stress_steel = force_steel/A

strain_al = df_al['CH5'].to_numpy()*0.01
strain_steel = df_steel['CH5'].to_numpy()*0.01

Vykreslení závislosti

Nyní, když máme data z tahového testu připravena, můžeme vytvořit rychlý graf pomocí metody ax.plot() knihovny Matplotlib. První pár hodnot (x, y), který předáme do ax.plot(), je ( strain_al}, stress_al), a druhý pár (x, y), který předáme, je (strain_steel, stress_steel). Příkaz plt.show() zobrazí graf.

fig,ax = plt.subplots()

ax.plot(strain_al, stress_al, strain_steel, stress_steel)

plt.show()

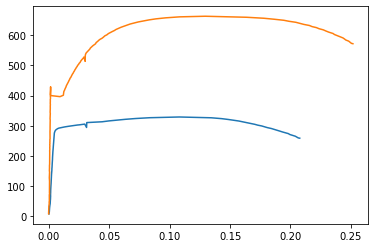
Náš graf vylepšíme přidáním popisek jednotlivých křivek a os.

Matplotlib metoda	Popis	Příklad
ax.set_xlabel()	popisek osy x	plt.xlabel(‘strain (in/in)’)
ax.set_ylabel()	popisek osy y	plt.ylabel(‘stress (ksi)’)
ax.set_title()	poisek grafu	plt.title(‘Stress Strain Curve’)
ax.legend()	legenda	plt.plt(x,y, label=’steel’)

fig,ax = plt.subplots()

ax.plot(strain_al, stress_al)
ax.plot(strain_steel, stress_steel)

ax.set_xlabel('Poměrná deformace (m/m)')
ax.set_ylabel('Napětí (MPa)')
ax.set_title('Smluvní tahový diagram  slitiny hliníku 6061 a oceli 1018')
ax.legend(['Al6061','Steel1018'])

plt.show()

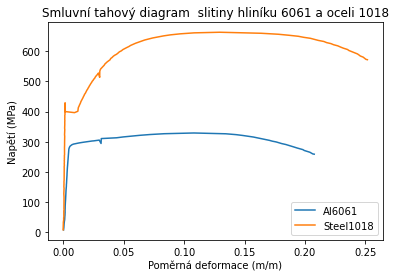
Nyní můžeme uložit graf jako obrázek ve formátu .png pomocí metody plt.savefig() knihovny Matplotlib. Kód níže vytvoří graf a uloží obrázek s názvem tahovy_diagram.png. Argument dpi=300 uvnitř metody plt.savefig() specifikuje rozlišení uloženého obrázku. Obrázek bude uložen ve složce static stejného adresáře jako náš kód.

fig,ax = plt.subplots()

ax.plot(strain_al, stress_al, label = 'Al6061')
ax.plot(strain_steel, stress_steel, label = 'Steel1018')

ax.set_xlabel('Poměrná deformace (m/m)')
ax.set_ylabel('Napětí (MPa)')
ax.set_title('Smluvní tahový diagram  slitiny hliníku 6061 a oceli 1018')
ax.legend()

plt.savefig('static/tahovy_diagram.png', dpi=300)
plt.show()

Nalezení meze pevnosti

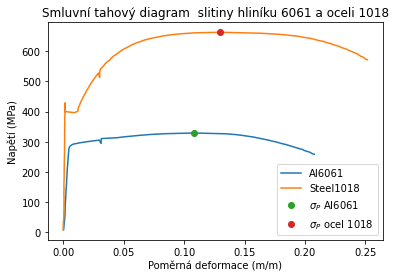
Mez pevnosti je bod na grafu s největší hodnotou napětí.

uts_steel = np.max(stress_steel)
uts_al = np.max(stress_al)

Pro vykreslení dodáme ještě deformace, ve kterých nastává mez pevnosti

uts_strain_steel = strain_steel[stress_steel==uts_steel][0]
uts_strain_al = strain_al[stress_al==uts_al][0]



print(f'Mez pevnosti pro hliník 6061 je {uts_al} MPa a nastává při poměrném prodloužení {uts_strain_al}.')
print(f'Mez pevnosti pro ocel 1018 je {uts_steel} MPa a nastává při poměrném prodloužení {uts_strain_steel}.')

Mez pevnosti pro hliník 6061 je 328.87169171951257 MPa a nastává při poměrném prodloužení 0.10797487258911133.
Mez pevnosti pro ocel 1018 je 663.4758721964481 MPa a nastává při poměrném prodloužení 0.12940356254577637.

Body si můžeme přidat do grafu.

fig,ax = plt.subplots()

ax.plot(strain_al, stress_al, label = 'Al6061')
ax.plot(strain_steel, stress_steel, label = 'Steel1018')

ax.plot(uts_strain_al, uts_al, "o", label = '$\sigma_P$ Al6061')
ax.plot(uts_strain_steel, uts_steel, "o", label = '$\sigma_P$ ocel 1018')


ax.set_xlabel('Poměrná deformace (m/m)')
ax.set_ylabel('Napětí (MPa)')
ax.set_title('Smluvní tahový diagram  slitiny hliníku 6061 a oceli 1018')
ax.legend()

plt.savefig('static/tahovy_diagram.png', dpi=300)
plt.show()

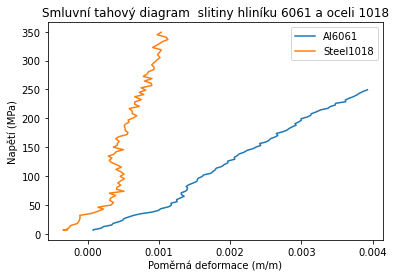
Určení Youngova modulu pružnosti

Zvolíme si část křivky, pro kterou je průběh lineárrní. Pro slitinu hliníku to bude přibližně oblast mezi 0 a 250 MPa a pro ocel mezi 0 a 350 MPa.

lin_stress_steel = stress_steel[stress_steel<350]
lin_strain_steel = strain_steel[stress_steel<350]

lin_stress_al = stress_al[stress_al<250]
lin_strain_al = strain_al[stress_al<250]

fig,ax = plt.subplots()

ax.plot(lin_strain_al, lin_stress_al, label = 'Al6061')
ax.plot(lin_strain_steel, lin_stress_steel, label = 'Steel1018')

ax.set_xlabel('Poměrná deformace (m/m)')
ax.set_ylabel('Napětí (MPa)')
ax.set_title('Smluvní tahový diagram  slitiny hliníku 6061 a oceli 1018')
ax.legend()

<matplotlib.legend.Legend at 0x73e1dd2eb010>

V jednoduchém přístupu použijeme funkci aproximace bodů polynomem prvního stupně.

param_steel = np.polyfit(lin_strain_steel, lin_stress_steel, 1)
param_al = np.polyfit(lin_strain_al, lin_stress_al, 1)

print(f'Ocel 1018: Napětí = {param_steel[1]} + {param_steel[0]} * deformace')
print(f'Al6061: Napětí = {param_al[1]} + {param_al[0]} * deformace')

Ocel 1018: Napětí = 30.353246542441244 + 267660.33488346846 * deformace
Al6061: Napětí = -13.32484752659266 + 68493.0090973414 * deformace

A zpětné získáme fitovaná data.

fit_stress_steel = np.polyval(param_steel, lin_strain_steel)
fit_stress_al = np.polyval(param_al, lin_strain_al)

fig,ax = plt.subplots()

ax.plot(lin_strain_al, lin_stress_al, label = 'Al6061')
ax.plot(lin_strain_steel, lin_stress_steel, label = 'Steel1018')
ax.plot(lin_strain_al, fit_stress_al,"--" ,label = 'fit Al6061')
ax.plot(lin_strain_steel, fit_stress_steel,"--", label = 'fit Steel1018')

ax.set_xlabel('Poměrná deformace (m/m)')
ax.set_ylabel('Napětí (MPa)')
ax.set_title('Smluvní tahový diagram  slitiny hliníku 6061 a oceli 1018')
ax.legend()

<matplotlib.legend.Legend at 0x73e1dd366020>

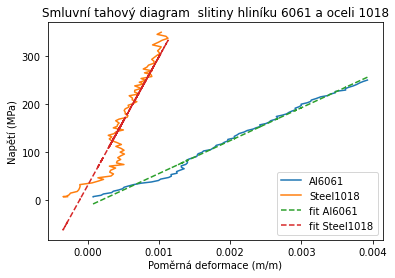
Sklon přímky nám udáva hodnotu Youngova modulu pružnosti.

print(f'E(ocel 1018) = {param_steel[0]/1000} GPa')
print(f'E(Al6061) = {param_al[0]/1000} GPa')

E(ocel 1018) = 267.66033488346847 GPa
E(Al6061) = 68.4930090973414 GPa

Výsledky můžeme srovnat s výsledky v tabulkách, např. matweb.com nebo asm.matweb.com. Na základě našich měření a hodnot v tabulkách se můžeme pokusit odhadnout o jaký typ zpracování oceli 1018 se jedná.

Alternativou je využití složitějších modelů k fitování křivek, například knihovna lmfit.

def model_hooke(epsilon, E):
    return epsilon * E

emodel = Model(model_hooke)

result = emodel.fit(lin_stress_steel, epsilon=lin_strain_steel, E=0*1e3)

print(result.fit_report())

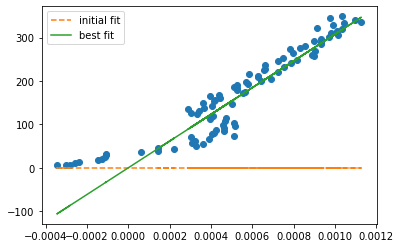
plt.plot(lin_strain_steel, lin_stress_steel, 'o')
plt.plot(lin_strain_steel, result.init_fit, '--', label='initial fit')
plt.plot(lin_strain_steel, result.best_fit, '-', label='best fit')
plt.legend()
plt.show()

print(f'E(ocel 1018) = {result.params["E"]/1000} GPa')

[[Model]]
    Model(model_hooke)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 13
    # data points      = 91
    # variables        = 1
    chi-square         = 139374.949
    reduced chi-square = 1548.61055
    Akaike info crit   = 669.399783
    Bayesian info crit = 671.910643
    R-squared          = 0.84966458
[[Variables]]
    E:  307574.304 +/- 6556.48153 (2.13%) (init = 0)

E(ocel 1018) = 307.57430351056655 GPa