7. cvičení

Momenty stervačnosti geometrických těles

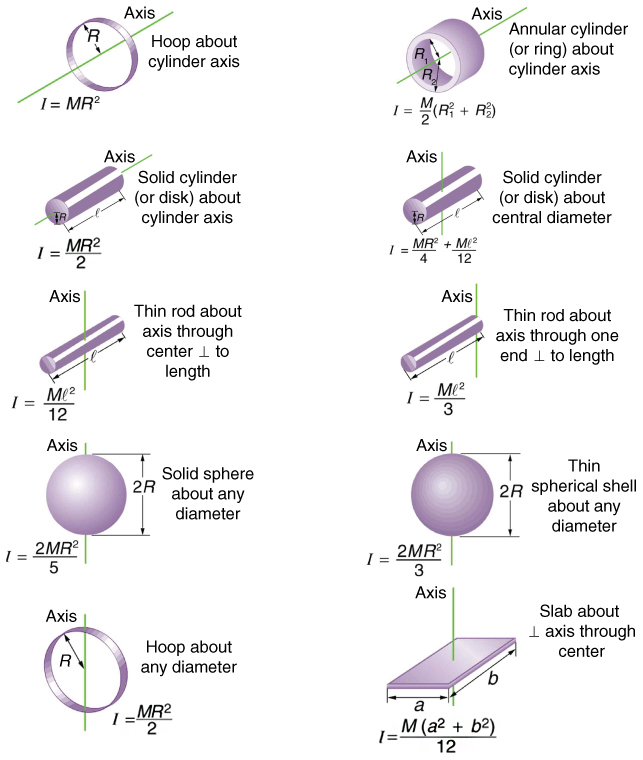
Moment setrvačnosti

1. Určete momenty setrvačností tenké homogenní tyče hmotnosti m a délky L s osou otáčení procházející:

   • středem tyče (analyticky)

   • koncem tyče (analyticky)

   • koncem tyče pomocí Steinerovy věty

   • bodem v jedné čtvrtině délky tyče metodou podle své volby

   Řešení

2. Určete moment setrvačnosti u tělesa podle obrázku když \(m_1=2m_2=m_3-2=2m_4=2kg\). Když se otáčí

   • kolem osi \(x\)

   • kolem osi \(y\)

   • kolem osi \(z\)

   Velikost koulí můžete zanedbat.

   

Pohybové rovnice

1. Uvažujme otce, jak tlačí kolotoč na hřišti na obrázku 4. Působí silou 250 N na okraj 50,0 kg vážícího kolotoče, který má poloměr 1,50 m. Vypočítejte úhlové zrychlení vzniklé

   • když na kolotoči nikdo není, a

   • když 18,0 kg vážící dítě sedí 1,25 m od středu. Samotný kolotoč považujte za jednolitý kotouč se zanedbatelným retardačním třením.

   

   Řešení

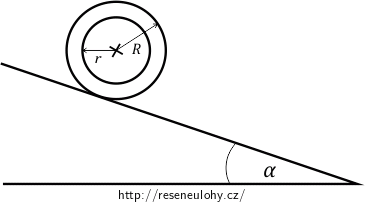
2. Betonová válcová skruž o hmotnosti \(M\) se valí bez smýkání dolů po svahu, který svírá s vodorovnou rovinou úhel \(\alpha\)

• Určete moment setrvačnosti skruže, je-li její vnější poloměr \(R\), vnitřní poloměr \(r\)

• Určete zrychlení hmotného středu skruže. Řešte pmocí pohybových rovnic, viz. přednášky.

Řešení

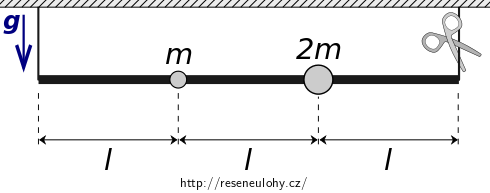
3. Tyč o délce \(3l\), jejíž hmotnost zanedbáváme, je zavěšena ve vodorovné poloze pomocí dvou vláken, upevněných na koncích tyče. Na tyči jsou nasazeny malé koule o hmotnostech \(m\) a \(2m\) tak, že jejich středy leží v jedné, resp. dvou třetinách délky tyče. Poloměry koulí jsou malé oproti délce tyče.

   

   Řešení

4. Automobilový motor může produkovat točivý moment 200 Nm. Vypočítejte úhlové zrychlení kola, pokud 95,0 % tohoto točivého momentu působí na hnací hřídel, nápravu a zadní kola automobilu, s ohledem na následující informace. Auto je zavěšeno tak, aby se kola mohla volně otáčet. Každé kolo se chová jako 15,0 kg disk s poloměrem 0,180 m. Stěny každé pneumatiky fungují jako 2,00 kg vážící prstenec, který má vnitřní poloměr 0,180 m a vnější poloměr 0,320 m. Běhoun každé pneumatiky působí jako 10,0 kg obruč o poloměru 0,330 m. Osa kol o hmotnosti 14,0 kg funguje jako tyč s poloměrem 2,00 cm. Hnací hřídel o hmotnosti 30,0 kg funguje jako tyč s poloměrem 3,20 cm.

Energie rotačního pohybu

1. Osoba, jejíž noha je znázorněna na obrázku, kopne nohou vyvinutím svalové síly 2000 N. Účinné kolmé rameno svalu je 2,20 cm. Vzhledem k tomu, že moment setrvačnosti bérce je 1,25 kg⋅m\(^2\)

   • najděte úhlové zrychlení nohy.

   • Zanedbáme-li gravitační sílu, jaká je rotační kinetická energie nohy poté, co se otočila o 57,3\(^\circ\) (1,00 rad)?

   

   Řešení

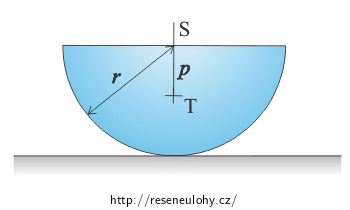
2. Homogenní půlválec o poloměru r a hmotnosti m leží na vodorovné rovině.

   • Určete moment setrvačnosti půlválce vzhledem k přímce, ve které se půlválec dotýká roviny.

   • Půlválec vykloníme o malý úhel z rovnovážné polohy a pustíme. S jakou periodou se bude kolébat?

   

   Řešení

Zákon zachování momentu hybnosti

1. Obrázek ukazuje otáčivý podnos s jídlem. Předpokládejme, že osoba vyvíjí sílu 2,50 N kolmo na poloměr podnosu 0,260 m po dobu 0,150 s.

   • Jaký je konečný moment hybnosti, pokud začíná z klidu, za předpokladu, že tření je zanedbatelné?

   • Jaká je konečná úhlová rychlost podnosu za předpokladu, že její hmotnost je 4,00 kg a za předpokladu, že její moment setrvačnosti je momentem setrvačnosti disku?

   

   Řešení

2. Předpokládejme, že bruslařka, jako je ta na obrázku, se točí rychlostí 0,800 ot/s s nataženými pažemi. Má moment setrvačnosti 2,34 kg m\(^2\) s nataženými pažemi a 0,363 kg m\(^2\) s rukama u těla. (Tyto momenty setrvačnosti jsou založeny na rozumných předpokladech o bruslaři o hmotnosti 60,0 kg.)

   • Jaká je její úhlová rychlost v otáčkách za sekundu poté, co přitáhne ruce?

   • Jaká je její rotační kinetická energie před a poté, co to udělá?

   • Proč se kinetická energie změnila?

   

   Řešení

3. Dřevěná tyč délky 40 cm a hmotnosti 1 kg se může otáčet kolem osy kolmé na tyč a procházející jejím středem. Na konec tyče narazí střela o hmotnosti 10 g a rychlosti 200 m·s\(^{-1}\) ve směru kolmém na osu i na tyč. Určete úhlovou rychlost, kterou se tyč dá do pohybu, když v ní střela uvázne.

   

   Řešení

4. Na obvodu nehybné vodorovné homogenní kruhové desky o hmotnosti 140 kg a poloměru 4 m, volně otáčivé kolem svislé osy ve středu, stojí punker o hmotnosti 79 kg se dvěma kilogramovými závažími v rukou.

   • S jakou úhlovou rychlostí se začne deska otáčet, odhodí-li punker jedno závaží ve směru tečném k obvodu desky s počáteční rychlostí 20 m·s\(^{-1}\)?

   • Jaká bude úhlová rychlost desky, přejde-li punker poté o 2 m blíž k ose?

   • Jaká bude úhlová rychlost desky, odhodí-li punker druhé závaží podobně jako to první, rychlostí 20 m·s\(^{-1}\) vzhledem k rotující desce?

   

   Řešení

5. Astronaut utahuje šroub na satelitu na oběžné dráze. Otáčí se v opačném směru, než je směr šroubu, a satelit se otáčí stejným směrem jako šroub. Vysvětlete proč. Pokud je na satelitu k dispozici držadlo, lze této protirotaci zabránit? Vysvětlete svou odpověď.