Tahová zkouška

from IPython.display import IFrame
from IPython.display import YouTubeVideo

Tahová zkouška

Tahová zkouška je destruktivní mechanická zkouška materiálu, která slouží k určení jeho mechanických vlastností při tahovém zatížení. Při zkoušce se zkušební vzorek upne do trhacího stroje a postupně se zatěžuje tahovou silou. Během zkoušky se měří prodloužení vzorku a síla, která na něj působí. Z naměřených dat se pak sestavuje tahový diagram, ze kterého se vyhodnocují mechanické vlastnosti materiálu.

Všeobecně se rozlišují zkoušky tahem pod

• statickým zatížením - stálé konstantní zatížení

• kvazistatickým zatížením - zatížení plynule narůstá a působí plynule (kvazistaticky). Horní mez pro kvazistatické zkušební metody se pohybuje na rychlosti deformace přibližně 10-1/s, proto maximální nárůst (např. deformace) nesmí být větší než 0,1 % / s

• cyklickým zatížením - zatížení se periodicky mění

• rázovým zatížením - prudká změna zatížení

Postup zkoušky

1. Příprava vzorku: Z materiálu se vyrobí zkušební vzorek normalizovaných rozměrů a tvaru.

2. Upnutí vzorku: Vzorek se upne do čelistí trhacíhbo stroje.

3. Zatěžování vzorku: Vzorek se postupně zatěžuje tahovou silou.

4. Měření dat: Během zkoušky se měří prodloužení vzorku a působící síla.

5. Sestavení diagramu: Z naměřených dat se sestaví tahový diagram, který zobrazuje závislost napětí na deformaci.

6. Vyhodnocení parametrů: Z tahového diagramu se vyhodnotí mechanické vlastnosti materiálu.

Tahový diagram

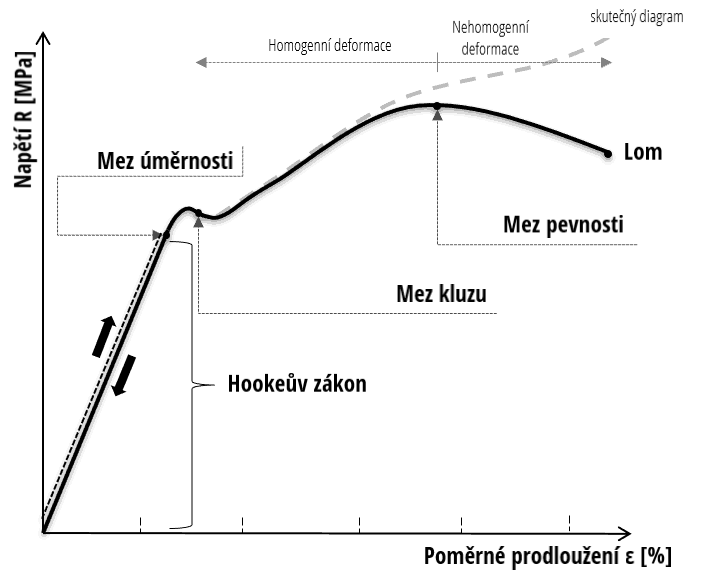
Průběh zkoušky je graficky zaznamenán pomocí tahového diagramu, který je závislostí síly (napětí) na prodloužení (poměrném prodloužení) zkušebního tělesa. Rozlišujeme tři typy tahového diagramu:

1. diagram pracovní - závislost síly \(F\) na prodloužení \(\Delta l\))

2. diagram smluvní - závislost smluvného napětí \(\sigma_s\) na poměrném prodloužení \(\varepsilon\), vztažená k původním rozměrům vzorku) a

3. diagram skutečný - závislost skutečného napětí \(\sigma\) na skutečném prodloužení \(\epsilon\), vztažená ke skutečným aktuálním rozměrům vzorku v průběhu zkoušky.

Nejčastěji se využívá smluvní tahový diagram. Smluvní napětí \(\sigma_s\) je dáno vztahem

\[\sigma_s = \frac{F}{A_0}\]

kde \(F\) je zatěžující síla a \(A_0\) je původní průřez zatěžovaného vzorku. Poměrné podélné prodloužení \(\varepsilon\) definované vztahem

\[\varepsilon = \frac{\Delta l}{l_0} = \frac{l - l_0}{l_0}\]

kde \(l\) je délka vzorku po zatížení silou \(F\) a \(l_0\) je původní délka vzorku.

1. Elastická oblast

   • Vztah mezi napětím a deformací je lineární.

   • Po odstranění zatížení se materiál vrátí do původního tvaru.

   • Materiál se řídí Hookeovým zákonem a platí přímá úměrnost mezi napětím a deformací.

   • Směrnice přímky v této oblasti definuje důležitou materiálovou vlastnost – Youngův modul pružnosti (modul pružnosti v tahu).

2. Přechod do plastické oblasti

   • Při dosažení určitého napětí materiál přechází z elastické do plastické oblasti.

   • Mez kluzu označuje napětí, při kterém začíná trvalá (plastická) deformace.

   • Elastické deformace jsou vratné, plastické deformace nejsou vratné.

3. Krčkování a lom materiálu

   • Při krčkování (necking) dochází k nerovnoměrné plastické deformaci, při které se část vzorku výrazně ztenčuje.

   • V této oblasti vznikají vysoké koncentrace napětí, což vede ke konečnému lomu materiálu.

   • Po lomu lze vypočítat procentuální prodloužení a celkové zmenšení průřezu vzorku.

Caution

Skutečné napětí není rovno smluvnému napětí V průběhu zkoušky dochází ke změně průřezu. Proto se skutečné napětí liší od smluvného napětí, při kterém se počítá s původní plochou průřezu.

YouTubeVideo('67fSwIjYJ-E', width=800)

Parametry vyhodnocované z tahové zkoušky

Parametr	Meze / Hodnoty	Označení (ASTM)	Označení (ISO)	Definice
Mez úměrnosti (Proportional Limit)	\(\sigma_u\) (MPa)	PL	-	Nejvyšší napětí, při kterém je napětí úměrné deformaci podle Hookeova zákona.
Mez pružnosti (Elasticity Limit)	\(\sigma_e\) (MPa)	EL	-	Mezní napětí, které po odtížení ( odlehčení ) nevyvolává trvalé deformace
Modul pružnosti (Young’s Modulus)	E (GPa)	E	E	Poměr mezi napětím a deformací v elastické oblasti, určuje tuhost materiálu.
Mez kluzu (Yield Strength)	\(\sigma_k\), \(\sigma_y\) (MPa)	YS	Re	Napětí, při kterém materiál přechází z elastické do plastické oblasti.
Mez pevnosti v tahu (Ultimate Tensile Strength)	\(\sigma_{UTS}, \sigma_P\) (MPa)	UTS	Rm	Nejvyšší dosažené napětí během tahové zkoušky před nástupem krčkování.
Procentuální prodloužení (Elongation at Break)	A (%)	EL	A	Relativní prodloužení vzorku při lomu vyjádřené v procentech původní délky.
Kontrakce průřezu (Reduction of Area)	Z (%)	RA	Z	Relativní zmenšení průřezu vzorku při lomu, vyjádřené v procentech původní plochy.
Skutečné napětí při lomu (True Fracture Stress)	σ_f (MPa)	TFS	-	Skutečné napětí vypočtené s ohledem na skutečný zmenšený průřez v místě lomu.

• Mez kluzu (\(\sigma_Y\)): Napětí, při kterém dochází k náhlému plastickému toku materiálu (trvalé deformaci) bez nárůstu zatížení.

  \[\sigma_Y = \frac{F_Y}{A}\]

  kde

  • \(F_{Y}\) je síla kluzu.

  • \(A\) je počáteční průřez vzorku.

  Mez kluzu materiálů často není výrazná, a proto ji nelze při zkoušce tahem jednoznačně určit. V takových případech se vyhodnocuje smluvní mez kluzu. Smluvní mez kluzu se zpravidla určuje při plastickém prodloužení 0,2 %, proto se tato charakteristická hodnota označuje Rp0,2. V mnoha případech je možné stanovit jak hodnotu horní meze kluzu ReH, tak dolní meze kluzu ReL.

  

• Pevnost v tahu (\(\sigma_{UTS}\)): Maximální napětí, které materiál snese, než dojde k porušení.

  \[ \sigma_{UTS} = \frac{F_{max}}{A} \]

  kde

  • \(F_{max}\) je maximální síla.

  • \(A\) je počáteční průřez vzorku.

  U kovových materiálů s výraznou mezí kluzu je maximální tahová síla definována jako nejvyšší dosažená síla až za oblastí s mezí kluzu. Maximální tahová síla po překročení meze kluzu může u méně zpevněných materiálů ležet i pod mezí kluzu, v tomto případě je pak mez pevnosti v tahu nižší než hodnota horní meze kluzu.

Tahový diagram pro různé materiály

Tahový diagram je grafické znázornění závislosti napětí na deformaci. Pro různé materiály má diagram typický tvar, který se liší v závislosti na jejich vlastnostech.

• Křehké materiály (brittle): Mají lineární tahový diagram a po překročení meze pevnosti dochází k náhlému lomu bez výrazných plastických deformací.

• Houževnaté (tažné) materiály (ductile): Mají nelineární tahový diagram a po překročení meze kluzu dochází k plastickým deformacím, než dojde k lomu.

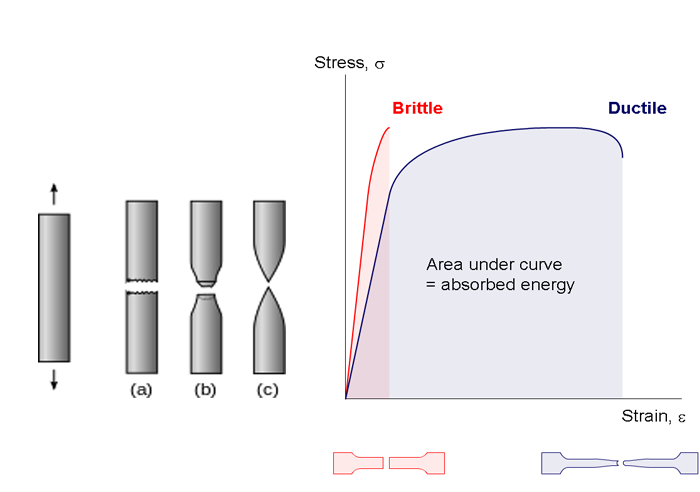
Houževnaté materiály

• Absorpce energie: Tažné materiály mohou absorbovat značné množství energie díky své schopnosti procházet plastickou deformací před zlomením.

• Deformace: Tyto materiály vydrží značné plastické deformace, než dojde k jejich zlomení.

• Křivka napětí-deformace: Křivka napětí-deformace tažných materiálů prochází všemi fázemi, jak bylo popsáno výše, včetně elastické deformace, kluzu, zpevnění a neckingu před zlomením.

• Příklady: Měkká ocel, hliník, měď, guma a většina plastů.

Křehké materiály

• Chování při zlomení: Křehké materiály se lámou bez výrazné změny v prodloužení nebo plastické deformaci. Jejich křivka napětí-deformace je po mezní síle téměř vertikální, což naznačuje velmi malou plastickou deformaci.

• Konzistence pevnosti: U křehkých materiálů jsou mez kluzu, mez pevnosti a mez porušení v podstatě stejné.

• Příklady: Lité železo, keramika, sklo, beton a kámen.