4. cvičení#
Superpozice pohybů#
Loď pluje po řece proti jejímu proudu z bodu A do bodu B a zpět do bodu A znovu. Rychlost lodi vůči vodě je v obou případech stejná a rovná se 4 km·h\(^{−1}\). Rychlost proudu je 1,6 km·h\(^{-1}\). Určete poměr času, který loďce zabere plavba z bodu A do bodu B a zpět, a doby, kterou by loď potřebovala na ujetí stejné vzdálenosti na klidném jezeře.
Basketbalový koš je umístěn ve výšce \(h_1\) nad podlahou. Střed koše je ve vzdálenosti \(L\) vodorovně od čáry trestného hodu. Basketbalista střílí trestné hody a míč opustí jeho ruku v okamžiku, kdy je jeho střed přesně nad čarou trestného hodu ve výšce \(h_2\) nad podlahou. Optimální elevační úhel \(\alpha\) je úhel, ve kterém střed míče prochází středem obruče, přičemž je potřeba minimální počáteční rychlost míče. Obecně dokažte, že tento úhel je \(\alpha = 45˚+\beta/2\), kde \(\beta\) je tečný úhel, tj. úhel směrnice přímky spojující střed obruče a počáteční bod výstřelu od vodorovné roviny.
Nádrž má dva otvory vyvrtané ve stěně, první ve výšce \(h_1\) měřeno ode dna a druhý ve výšce \(h_2\). V jaké výšce h musí být hladina vody v nádrži, pokud chceme, aby proudy vody proudily z obou otvorů, abychom získali stejný dosah \(x\)? Odpor vzduchu je zanedbatelný. Rěšte úlohu obecně, pak pro hodnoty h1 = 10 cm a h2 = 30 cm.

Pohyb po kružnici#
Může člověk, který stojí na rovníku, „odlétnout“ účinkem odstředivé síly? Jak rychle by se musela točit Země, aby nám to hrozilo?
Kalibrovali jsme pružinovou váhu na severním pólu a poté jsme váhu přesunuli k rovníku. Udává stupnice stejné hodnoty jako na pólu? Uveďte důvody proč ano nebo ne.
Na kolotoči je na 1 m dlouhém provázku ve vzdálenosti 2 m od osy otáčení zavěšeno závaží o hmotnosti 0,5 kg. Závaží je vychýleno z klidové polohy o 10°. Závaží nekmitá. Jaká je doba rotace kolotoče? Vyřešte tento problém s ohledem na inerciální i neinerciální vztažnou soustavu.
Štíhlá tyč OA délky R se otáčí úhlovou rychlostí \(\omega\) ve směru hodinových ručiček v rovině kolem bodu O. Po tyči leze mravenec z bodu O do bodu A konstantní rychlostí \(\vec{v}(t)\) (měřeno s ohledem na tyč). Určete časově závislou polohu mravence v laboratorní referenční soustavě. Předpokládejme, že poloha v čase t = 0 s byla ve středu tyče.
Malé těleso klouže z nejvyššího bodu koule o poloměru \(R\) po povrchu koule bez tření.
A) V jaké výšce h pod nejvyšším bodem koule se těleso odpojí od povrchu koule?
B) Vypočítejte rychlost tělesa v okamžiku odpojení od povrchu koule, pokud mělo v nejvyšším bodě nulovou rychlost.
C) V jaké vzdálenosti od bodu dotyku míče s vodorovným stolem přistane těleso na stole?
Moment síly#
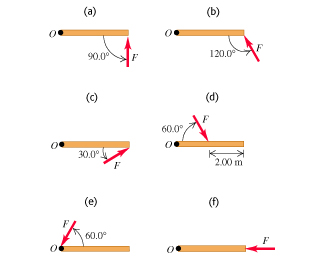
Která ze sil má největší otáčívý účinek. Vyjádřete matematicky pomocí momentu síly.
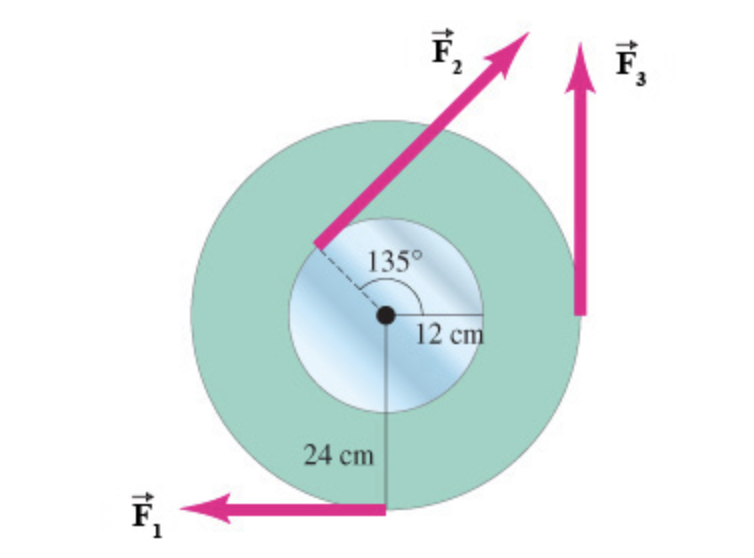
Vypočítejte čistý točivý moment kolem nápravy kola zobrazeného na obrázku. Předpokládejme, že třecí moment 0,50 Nm brání pohybu. Předpokládejme, že \(F_1\) = 22 N, \(F_2\) = 35 N, \(F_3\) = 21 N.
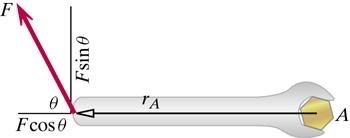
Pokud \(r_A\)=0,34 m, \(F\)=18 N a \(\theta\)=61°, jaká je velikost momentu kolem bodu A. Řešte pomocí vektorové algebery a rozkladem na složky.
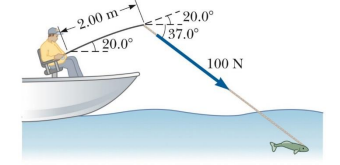
Lovíte na jezeře a chytáte rybu pěkné velikosti. Jaký točivý moment musíte udržet v ruce?
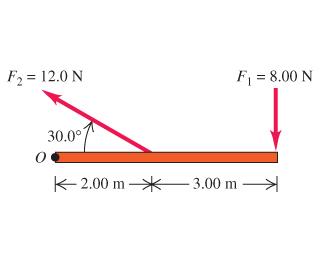
Určete výsledný moment síly k bodu 0
Určete výsledný moment síly k bodu C

Poloha těžiště#
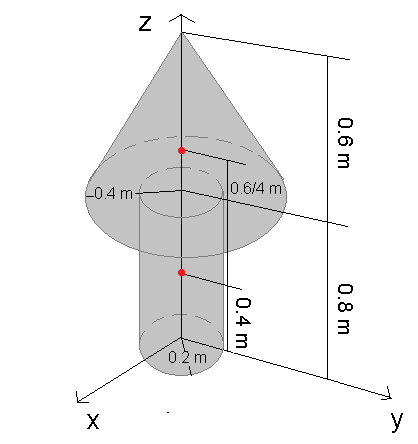
Určete polohu těžiště u objektu na obrázku.
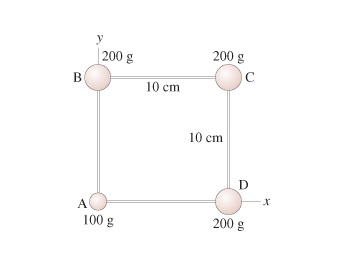
Určete polohu těžiště u objektu na obrázku.

Výpočtem určete polohu těžiště tenkého drátu o poloměru \(r\), který ohneme do podoby půlkružnice o poloměru \(R\) (\(r\ll R\)).
Určete polohu těžiště u objektu na obrázku.