Skutečné a smluvní napětí a deformace

import numpy as np
import matplotlib.pyplot as plt

V technické mechanice a pevnostní analýze se smluvní napětí a smluvní deformace používají pro popis materiálového chování. Tyto veličiny se zavádějí zejména v souvislosti s tažnými zkouškami a analýzou materiálových vlastností.

Smluvní napětí (engineering stress)

Smluvní napětí \(\sigma_s\) se definuje jako podíl aktuální síly \(F\) a počáteční plochy příčného řezu \(A_0\) před deformací:

\[ \sigma_s = \frac{F}{A_0} \]

kde:

• \(F\) je působící síla [N}],

• \(A_0\) je počáteční plocha průřezu před deformací [m].

Tento přístup zjednodušuje výpočty, protože při velkých plastických deformacích dochází k výrazné změně průřezu, což by komplikovalo výpočet skutečného napětí.

Rozdíl mezi smluvním a skutečným napětím

• Smluvní napětí – počítá s původním průřezem \(A_0\), což je běžné v inženýrských výpočtech.

• Skutečné napětí (true stress) – vychází z aktuální plochy průřezu \(S\) v daném okamžiku deformace, což je přesnější, ale složitější na výpočet:

\[ \sigma_t = \frac{F}{A} \]

kde \(A\) je skutečná plocha průřezu v okamžiku měření.

Smluvní deformace (engineering strain)

Smluvní (technická) deformace \((\varepsilon_s)\) se definuje jako podíl prodloužení délky a původní délky vzorku:

\[ \varepsilon_s = \frac{\Delta L}{L_0} \]

kde:

• \(\Delta L = L - L_0\) je změna délky [m],

• \(L_0\) je původní délka vzorku [m]).

Rozdíl mezi smluvní a skutečnou deformací

• Smluvní deformace – používá počáteční délku \(L_0\), což zjednodušuje výpočty.

• Skutečná (logaritmická) deformace (true strain) – bere v úvahu okamžitou délku (L), což je přesnější zejména pro velké deformace

Odvození vztahu logaritmické deformace

Vyjdeme z definice infinitesimálního přírůstku podélné deformace:

\[ d\varepsilon_t = \frac{dL}{L} \]

Integrací této rovnice v mezích od \(L_0\) (počáteční délka) po \(L\) (aktuální délka) získáme:

\[ \varepsilon_t = \int_{L_0}^{L} \frac{dL}{L} \]

Tento integrál je elementární a logaritmická deformace je dána vztahem:

\[ \varepsilon_t = \ln{\left( \frac{L}{L_0} \right)} \]

Vztah mezi logaritmickou a smluvní deformací

Pro malé deformace (\(\varepsilon_s \ll 1\)) se logaritmická deformace přibližně rovná smluvní deformaci:

\[ \ln(1 + \varepsilon_s) \approx \varepsilon_s, \quad \text{pro } \varepsilon_s \ll 1 \]

Pro velké deformace však platí:

\[ \varepsilon_t = \ln{\frac{L}{L_0}} = \ln\left({\frac{L0}{L_0} + \frac{L-L0}{L_0}}\right) = \ln(1 + \varepsilon_s) \]

Caution

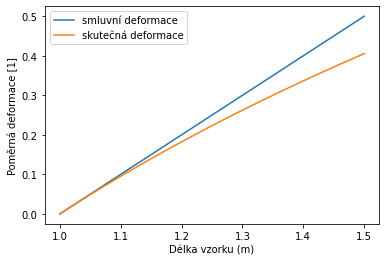
Logaritmická deformace je vždy o něco menší než smluvní deformace při větších hodnotách \(\varepsilon_s\).

L0 = 1
delta_L = 0.5
L = np.linspace(L0,L0 + delta_L,100)

epsilon_s = (L - L0)/L0
epsilon_t = np.log(L/L0)
# pro numpy log označuje přirozený logaritmus

plt.plot(L, epsilon_s, label = "smluvní deformace")
plt.plot(L, epsilon_t, label = "skutečná deformace")
plt.xlabel("Délka vzorku (m)")
plt.ylabel("Poměrná deformace [1]")
plt.legend()
plt.show()