Dynamika oscilátoru

import numpy as np
import matplotlib as plt

Proč vzniká kmitavý pohyb

Newtonovy zákony a oscilační pohyb:

První Newtonův zákon, zákon setrvačnosti, postuluje, že těleso setrvává v klidu nebo v rovnoměrném přímočarém pohybu, pokud na něj nepůsobí vnější síla. Z toho plyne, že oscilující těleso, měnící směr svého pohybu, je nutně vystaveno působení sil.

Analýza sil v oscilačním systému:

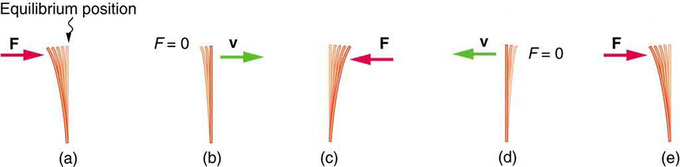
Uvažujme jednorozměrný oscilátor, jehož polohu popisuje souřadnice \(x\). Pokud oscilátor vykonává pohyb podél osy \(x\), pak v každém okamžiku platí:

• Když je \(x > 0\) (těleso vychýleno doprava), působí na něj síla \(F < 0\) (směřující doleva).

• Když je \(x < 0\) (těleso vychýleno doleva), působí na něj síla \(F > 0\) (směřující doprava).

Z této analýzy vyplývá existence bodu, kde \(F = 0\), což definuje rovnovážnou polohu systému. Konvenčně se počátek souřadnicového systému umisťuje do této rovnovážné polohy (\(x = 0\)).

Příklad: Oscilace plastového pravítka:

Demonstrativním příkladem oscilačního pohybu je vychýlení plastového pravítka z jeho stabilní vertikální polohy.

1. Vratná síla: Deformace pravítka indukuje vratnou sílu, která působí proti směru vychýlení. Tato síla se snaží vrátit pravítko do rovnovážné polohy.

2. Hybnost: Po uvolnění pravítka vratná síla urychluje jeho pohyb směrem k rovnovážné poloze. V důsledku hybnosti pravítko pokračuje v pohybu i po dosažení rovnovážné polohy, čímž dochází k vychýlení na opačnou stranu.

3. Tlumení: Reálné systémy jsou ovlivněny disipativními silami (např. třením), které postupně snižují amplitudu oscilací až do úplného zastavení pohybu.

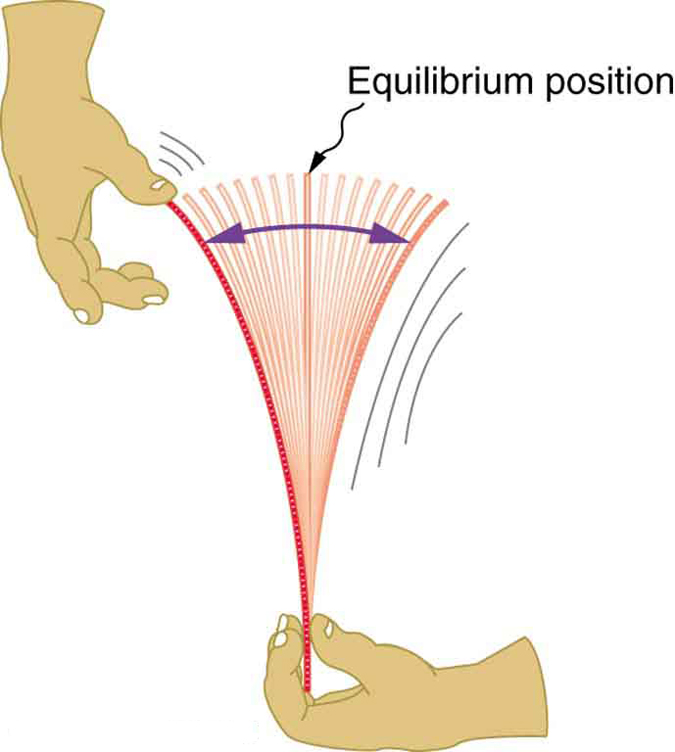
Dynamická analýza oscilačního cyklu:

1. Po vychýlení pravítka z rovnovážné polohy působí vratná síla, která ho urychluje zpět.

2. V rovnovážné poloze je výsledná síla nulová, ale pravítko má nenulovou hybnost, která ho unáší na opačnou stranu.

3. Na opačné straně působí vratná síla v opačném směru, čímž zpomaluje a zastavuje pohyb pravítka.

4. Proces se opakuje, přičemž amplituda oscilací se postupně snižuje v důsledku tlumení.

Pohybová rovnice oscilátoru

Pro jednorozměrný jednoduchý harmonický pohyb lze rovnici pohybu (což je lineární diferenciální rovnice druhého řádu s konstantními koeficienty) odvodit pomocí druhého Newtonova zákona a Hookeova zákona.

\[m \ddot{x} = -kx\]

kde \(m\) je hmotnost oscilujícího tělesa, \(x\) je jeho posunutí z rovnovážné polohy a \(k\) je konstanta pružiny. Proto:

\[\frac{d^2x}{dt^2} = -\left(\frac{k}{m}\right)x\]

Řešením výše uvedené diferenciální rovnice je sinusoidální funkce:

\[x(t) = c_1 \cos(\omega t) + c_2 \sin(\omega t)\]

• Použijeme součtový vzorec: \(\sin(\alpha + \varphi) = \sin(\alpha)\cos(\varphi) + \cos(\alpha)\sin(\varphi)\)

• Násobíme \(A\): \(A\sin(\alpha + \varphi) = A\sin(\alpha)\cos(\varphi) + A\cos(\alpha)\sin(\varphi)\)

• Porovnáme s původním výrazem:

  • \(c_1 = A\sin(\varphi)\)

  • \(c_2 = A\cos(\varphi)\)

• Odvodíme:

  • \(A = \sqrt{a^2 + b^2}\)

  • \(\varphi = \arctan\left(\frac{a}{b}\right)\)

Můžeme tedy řešení uvedené rovnice napsat ve tvaru:

\[x(t) = A \cos(\omega t - \varphi)\]

kde:

\[\omega = \sqrt{\frac{k}{m}}\]

\[A = \sqrt{c_1^2 + c_2^2}\]

\[\tan \varphi_0 = \frac{c_2}{c_1}\]

Caution

Součet dvou harmonických kmitů o stejné úhlové rychlosti je harmonický kmit se stejnou frekvencí a fázovým posuvem.

V řešení jsou \(c_1\) a \(c_2\) dvě konstanty určené počátečními podmínkami a počátek je nastaven v rovnovážné poloze. Každá z těchto konstant nese fyzikální význam pohybu: \(A\) je amplituda (maximální posunutí z rovnovážné polohy), \(\omega = 2\pi f\) je úhlová frekvence a \(\varphi_0\) je fáze.

Protože \(\omega = 2\pi f\), platí:

\[f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}\]

Vzhledem k tomu, že \(T = \frac{1}{f}\), platí:

\[T = 2\pi \sqrt{\frac{m}{k}}\]

Vlastní frekvence oscilátoru

Vlastní frekvence oscilátoru je frekvence, na které oscilátor přirozeně kmitá, když je vychýlen z rovnovážné polohy a uvolněn. Jinými slovy, je to frekvence, na které oscilátor kmitá bez působení vnější síly.

• Závisí na vlastnostech oscilátoru:

  • Vlastní frekvence je určena fyzikálními vlastnostmi oscilátoru (hmotnost, tuhost, délka, atd.).

• Nezávisí na amplitudě (u lineárních oscilátorů):

  • U ideálních oscilátorů je vlastní frekvence konstantní bez ohledu na amplitudu.