Deformace ve 2D

import numpy as np
from matplotlib import pyplot as plt

Poissonovo číslo

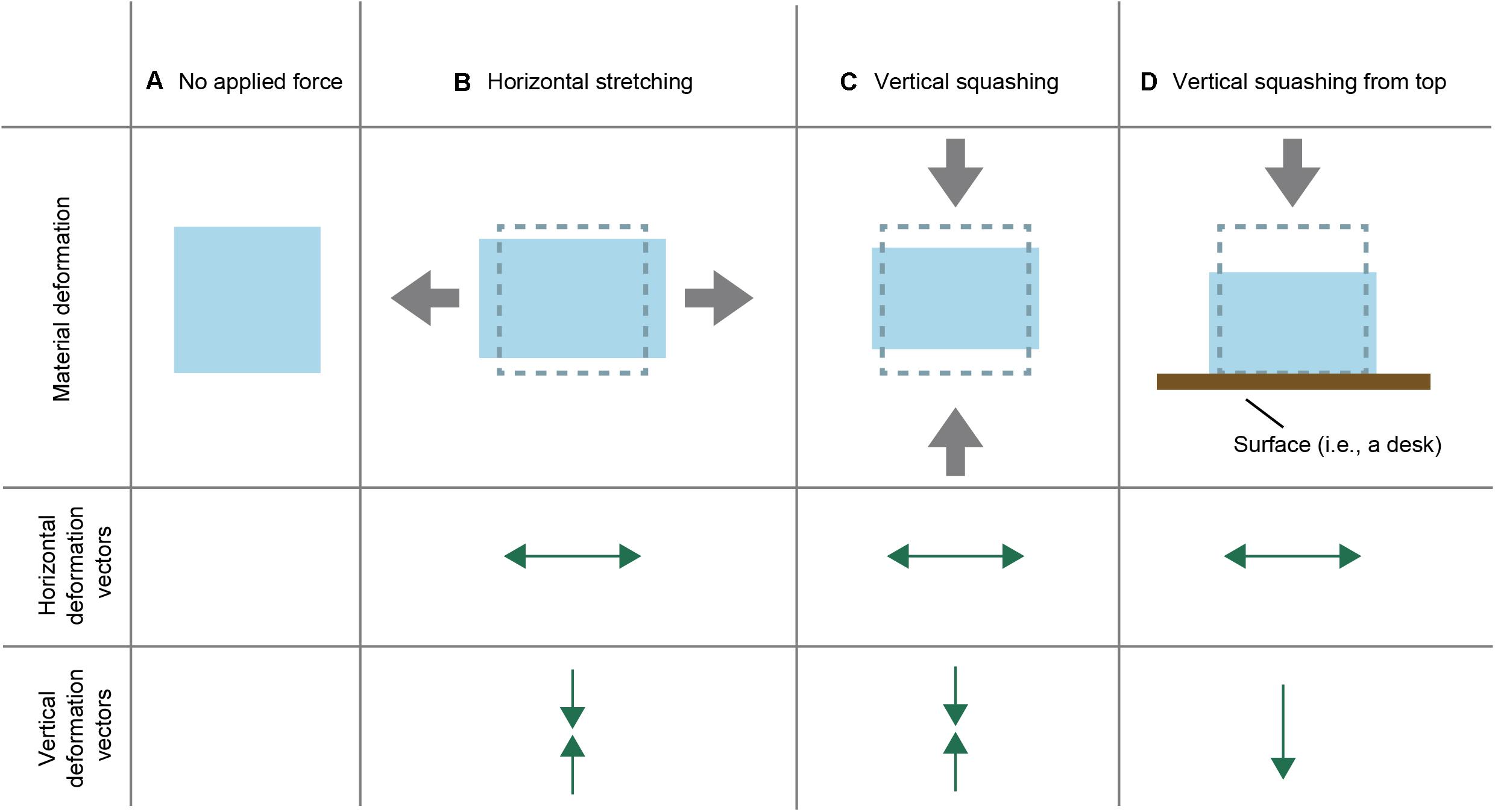
Poissonovo číslo (také Poissonův poměr) je bezrozměrná materiálová konstanta, která popisuje vztah mezi příčnou a podélnou deformací materiálu při mechanickém zatížení. Udává, jaký je poměr relativní změny šířky materiálu k relativní změně délky při tahovém nebo tlakovém namáhání.

Poissonovo číslo \(\nu\) je definováno jako záporný poměr příčné relativní deformace \(\varepsilon_{\perp}\) k podélné relativní deformaci \(\varepsilon_{\parallel}\):

\[ \nu = -\frac{\varepsilon_{\perp}}{\varepsilon_{\parallel}} \]

kde:

• \(\varepsilon_{\perp}\) je relativní deformace ve směru kolmém na směr zatížení,

• \(\varepsilon_{\parallel}\) je relativní deformace ve směru zatížení.

Podle https://doi.org/10.3389/fpsyg.2020.612368

Poissonovo číslo pro nestačitelný materiál

Materiál je nestlačitelný, pokud jeho objemová změna je nulová. Matematicky to znamená, že objemová deformace \(\varepsilon_V\) je nulová:

\[ \varepsilon_V = \frac{\Delta V}{V} = 0 \]

Objemová deformace je dána součtem hlavních normálových deformací:

\[ \varepsilon_V = \frac{l_x l_y l_z - l_{x0}l_{y0}l_{z0}}{l_{x0}l_{y0}l_{z0}} = \frac{(l_{x0} + \Delta l_x) (l_{y0} + \Delta l_y) (l_{z0} + \Delta l_z) - l_{x0}l_{y0}l_{z0}}{l_{x0}l_{y0}l_{z0}} = \varepsilon_x + \varepsilon_y + \varepsilon_z \]

Pro nestlačitelný materiál tedy platí:

\[ \varepsilon_x + \varepsilon_y + \varepsilon_z = 0 \]

Uvažujme tahové zatížení ve směru osy \(x\), tedy \(\varepsilon_x = \varepsilon_{\parallel}\). Vzhledem k symetrii se příčné deformace v osách \(y\) a \(z\) rovnají \(\varepsilon_y = \varepsilon_z = \varepsilon_{\perp}\).

Dosadíme do podmínky nestlačitelnosti:

\[ \varepsilon_x + 2\varepsilon_{\perp} = 0 \]

Vyjádříme \(\varepsilon_{\perp}\):

\[ \varepsilon_{\perp} = -\frac{\varepsilon_x}{2} \]

Dosadíme do definice Poissonova čísla:

\[ \nu = -\frac{\varepsilon_{\perp}}{\varepsilon_x} = -\frac{-\varepsilon_x / 2}{\varepsilon_x} = \frac{1}{2} \]

Pro nestlačitelný materiál platí:

\[ \nu = 0.5 \]

Typické hodnoty

Materiál	Poissonovo číslo \(\nu\)
Kovy	0.25 - 0.35
Ocel	0.3
Hliník	0.33
Sklo	0.2 - 0.3
Beton	0.1 - 0.2
Dřevo (vysoká vlhkost)	0.3
Dřevo (suché)	0.2
Plasty (typické)	0.3 - 0.4
Guma (elastomery)	0.49 - 0.5
Keramika	0.15 - 0.25
Pěnový materiál	-0.1 až -0.5 (auxetický)
Voda (vysoká tlaková)	0.5

Souvislost s modulem pružnosti

Poissonovo číslo ovlivňuje další mechanické vlastnosti materiálu. Pro izotropní materiály existuje vztah mezi Poissonovým číslem \(\nu\), Youngovým modulem pružnosti \(E\) a modulem pružnosti ve smyku \(G\):

\[ G = \frac{E}{2(1+\nu)} \]