Napětí při krutu

Hřídel je rotační strojní součást, která slouží k přenášení točivého momentu z jednoho místa na druhé.

Při krutu kruhového průřezu působí na materiál torzní (kroutící) moment, který vyvolává ve všech vláknech průřezu smykové napětí. Tento jev lze analyzovat pomocí vztahů pro kroutící moment a polární moment setrvačnosti.

Kroutící moment \( M_k \)

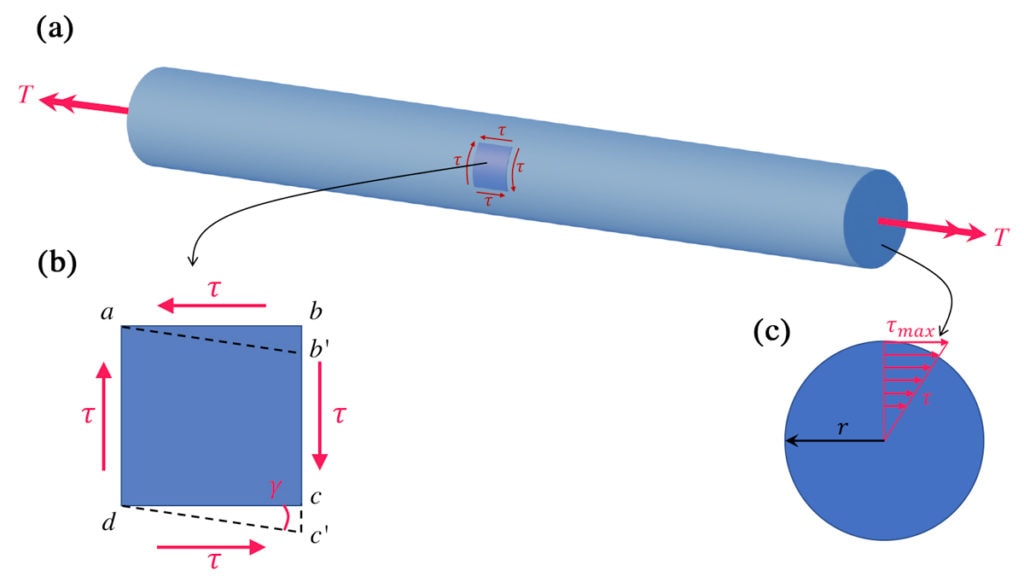
Kroutící moment \( M_k \) je moment, který působí na těleso kolem jeho osy a způsobuje, že se těleso otáčí.

U kruhového průřezu je tento moment definován jako:

\[ M_k = \int\limits_A \rho \tau \, dA \]

kde:

• \( M_k \) je kroutící moment,

• \( A \) je plocha průřezu,

• \( \rho \) je vzdálenost od osy otáčení (poloměr),

• \( \tau \) je smykové napětí v daném bodě průřezu.

Napětí při krutu

Předpokládáme, že napětí při krutu je minimální v ose hřídele a lineárně se zvyšuje směrem k okraji:

\[\tau = c \rho \]

Pro vztah mezi napětím a kroutícím momentem musí platit

\[ M_k = \int\limits_A c \rho^2 \, dA \]

z čeho platí

\[ c = \frac{M_k}{J_p} \]

kde \(J_p\) je polární kvadratický moment průřezu.

Pro výpočet smykového napětí \( \tau \) ve vláknech průřezu při působení kroutícího momentu používáme vztah:

\[ \tau = \frac{M_k r}{J_p} \]

kde:

• \( \tau \) je smykové napětí na vzdálenosti \( r \) od osy otáčení,

• \( M_k \) je kroutící moment,

• \( r \) je vzdálenost od osy otáčení (poloměr v daném bodě),

• \( J_p\) je polární kvadratický moment.

Tento vztah ukazuje, že smykové napětí je přímo úměrné vzdálenosti od osy otáčení a velikosti kroutícího momentu a nepřímo úměrné polárnímu momentu setrvačnosti.

Maximální napětí

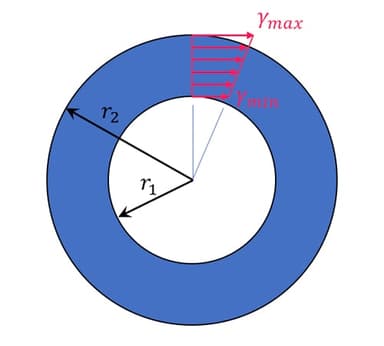
Maximální smykové napětí nastává na povrchu průřezu, kde \( r = R \) (poloměr kruhu). Maximální smykové napětí je tedy:

\[ \tau_{\text{max}} = \frac{M_k \cdot R}{J_p} \]

kde:

• \( R \) je poloměr kruhového průřezu.

Polární kvadratický moment \(J_p\)

Polární moment setrvačnosti \( J_p \) je geometrický moment, který popisuje odolnost průřezu proti krutu.

Pro kruhový průřez je definován jako:

\[ J_p = \int\limits_A \rho^2 \, dA \]

Pro kruhový průřez o poloměru \( R \) se polární moment setrvačnosti vypočítá jako:

\[ J_p = \frac{\pi R^4}{2} \]

kde:

• \( R \) je poloměr kruhu.