Napětí při ohybu

Nosník

Nosník je v konstrukčním inženýrství konstrukční prvek, který je navržen tak, aby přenášel zatížení ohybem kolmo na osu. Toto zatížení může zahrnovat jak statické zatížení (např. váha konstrukce), tak dynamické zatížení (např. zatížení větrem, pohybem).

Napětí vznikající při ohybu v materiálu je způsobeno ohybovým momentem, který působí na průřez materiálu. Pro výpočet napětí při ohybu využíváme ohybový moment \(M_o\) a kvadratický moment průřezu \(J_y\), který charakterizuje tuhost průřezu vůči ohybu.

Představme si, že máme prvek, který je ohýbán působením ohybového momentu \( M_o \). Tento moment vyvolává napětí ve všech vláknech průřezu. Napětí v určitém bodě průřezu závisí na jeho vzdálenosti od neutrální osy, která je osou, kolem které dochází k ohybu.

Neutrální osa

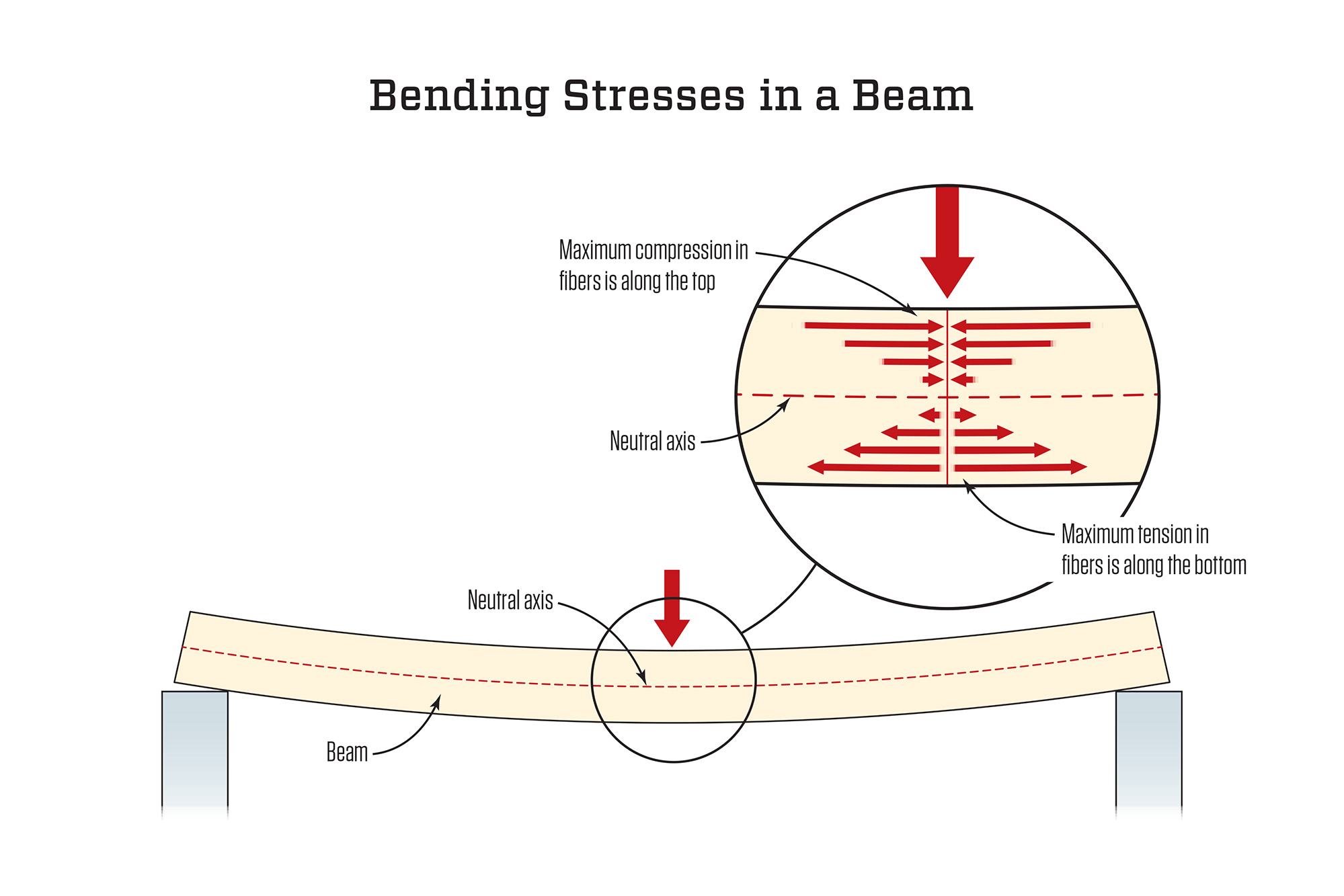
Neutrální osa je imaginární čára nebo rovina v materiálu, která není vystavena žádným normálním napětím při ohybu.

Na neutrální ose nedochází k žádné deformaci ve smyslu stlačení ani natažení — jde o místo, kde je napětí nulové. Při ohybu dochází k tomu, že části materiálu nad neutrální osou jsou stlačeny (získávají tlaková napětí), zatímco části pod neutrální osou jsou nataženy (mají tažná napětí).

Poloha neutrální osy

Poloha neutrální osy je ovlivněna geometrií průřezu a materiálovými vlastnostmi. Pro jednoduché výpočty se obvykle předpokládá, že neutrální osa je rovnoběžná s osou symetrie průřezu (například osou středu průřezu pro obdélníkové, kruhové a jiné symetrické průřezy). U různých typů průřezů je poloha neutrální osy dána různými faktory.

1. Pro symetrické průřezy (např. obdélníkový nebo kruhový průřez)

   • Neutrální osa je obvykle umístěna ve středu průřezu. U obdélníkového průřezu například neutrální osa prochází středem výšky \(h\), tedy v bodě \(y = \frac{h}{2}\).

2. Pro nesymetrické průřezy

   • U nesymetrických průřezů je neutrální osa také určena geometrickými a materiálovými vlastnostmi průřezu. Neutrální osa je často posunuta od osy symetrie, což znamená, že vznikají různé výpočty, které berou v úvahu tento posun.

Při ohybu materiálu platí, že napětí musí přenést ohybový moment a nepřenáší sílu. Velikost momentu síly od tahových a tlakových napětí musí být stejná.

\[ \int F = \int_A \sigma(y) dA = 0 \]

co je ekvivalentní definici težiště průřezu, když osa \(y=0\) prochází těžištěm. Z toho plyne, že neutrální osoa u homogenního materiálu prochází těžištěm průřezu.

Ohybová deformace a napětí

Při ohybu se vlákna nad neutrální osou stlačují, zatímco vlákna pod neutrální osou se natahují. Ohybová deformace v materiálu je přímo úměrná vzdálenosti \( y \) od neutrální osy. Napětí vzniklé v materiálu je dáno vztahem:

Podobně jako u krutu můžeme předpokládat

\[\sigma = c y \]

kde \(y\) je vzdálenost od neutrální osy

Caution

Záporná vzdálenost značí záporné napětí (tlak) v případě kladného ohybového momentu.

\[ M_o = \int M = \int_A y \sigma(y) dA = \int_A y \sigma(y) dA = \int_A c y^2 dA = c J_p \]

\[ \sigma = \frac{M_o \cdot y}{J_y} \]

kde:

• \( \sigma \) je napětí v bodě na průřezu,

• \( M_o \) je ohybový moment působící na prvek,

• \( y \) je vzdálenost daného bodu od neutrální osy,

• \( J_y \) je kvadratický moment průřezu podle osy \( y \).

Kvadratický moment průřezu \( J_y \)

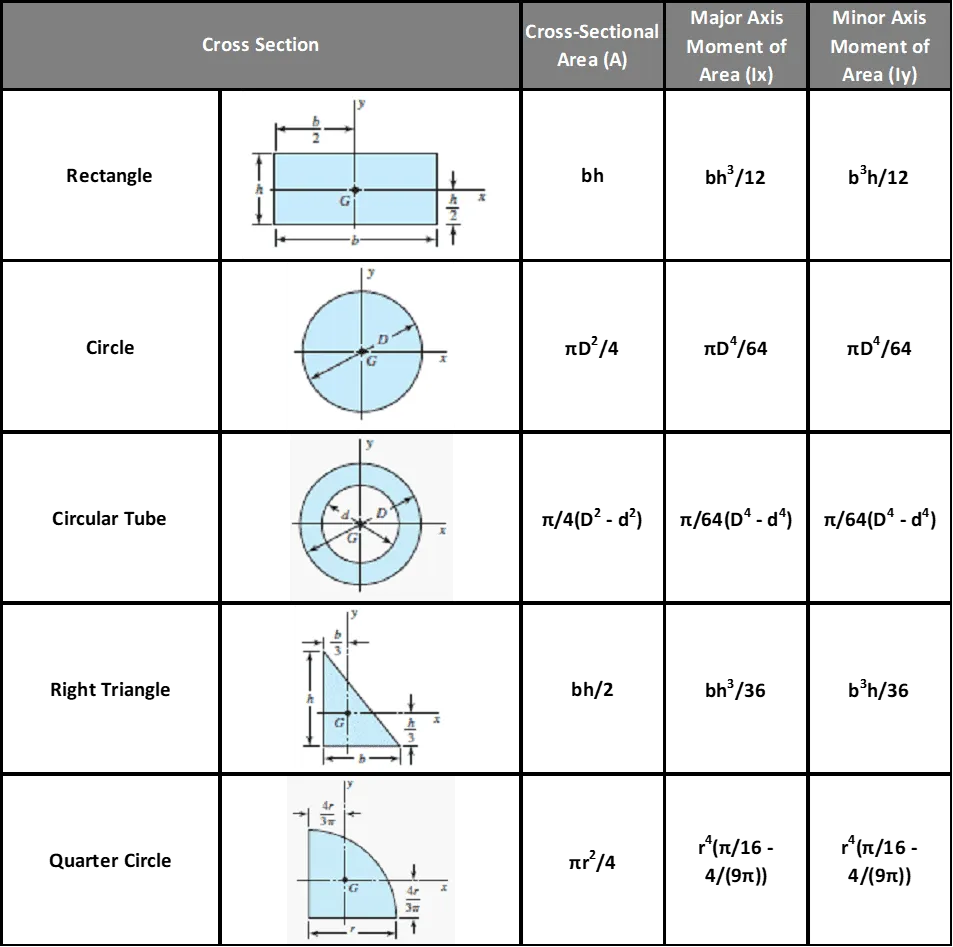
Kvadratický moment průřezu \( J_y \) je geometrická vlastnost, určuje odolnost vůči ohybu.

Kvadratický moment průřezu \( J_y \) je definován jako integrál vzdálenosti každého malého elementu plochy \( dA \) od osy \( y \) umocněné na druhou:

\[ J_y = \int_A y^2 \, dA \]

Pro různé geometrie průřezů existují specifické výrazy pro \( J_y \), např. pro obdélníkový průřez o šířce \( b \) a výšce \( h \) je:

\[ J_y = \frac{b h^3}{12} \]

Pro kruhový průřez o poloměru \( R \) je:

\[ J_y = \frac{\pi R^4}{4} \]

Maximální napětí při ohybu

Maximální napětí vznikne na okraji průřezu, kde je vzdálenost od neutrální osy \( y_{\text{max}} = R \) pro kruhový průřez nebo \( y_{\text{max}} = \frac{h}{2} \) pro obdélníkový průřez. Maximální napětí je tedy:

\[ \sigma_{\text{max}} = \frac{M_o \cdot y_\text{max}}{J_y} \]

Smykové napětí při ohybu

Pro výpočet smykového napětí při ohybu je potřeba zohlednit i smykové síly působící na materiál, které jsou způsobeny působící sílou. Pro jednoduchost, ve vztahu pro ohyb se soustředíme na normální napětí, které je při ohybu dominantní.