Mohrova kružnice#
import numpy as np
import math as mt
import matplotlib.pyplot as plt
import ipywidgets as widgets
from IPython.display import display
from IPython.display import IFrame
%config InlineBackend.print_figure_kwargs = {'bbox_inches':None}
%config InlineBackend.rc = {'font.size': 10, 'figure.figsize': (10.0, 6.0), 'figure.facecolor': (1, 1, 1, 0), 'figure.subplot.bottom': 0.125, 'figure.edgecolor': (1, 1, 1, 0), 'figure.dpi': 72}
%matplotlib inline
Hlavní napětí#
Hlavní napětí jsou taková normálová napětí působící na vzájemně kolmých rovinách, na nichž se nevyskytují smyková napětí. Jinými slovy, hlavní napětí jsou vlastní hodnoty tenzoru napětí a jejich směry (hlavní směry) odpovídají vlastním vektorům tohoto tenzoru.
Při odvozování Mohrovy kružnice se předpokládá, že svislé napětí \(\sigma_v\) a vodorovné napětí \(\sigma_h\) jsou hlavními napětími. Ve skutečnosti však mohou mít tato napětí libovolnou orientaci.
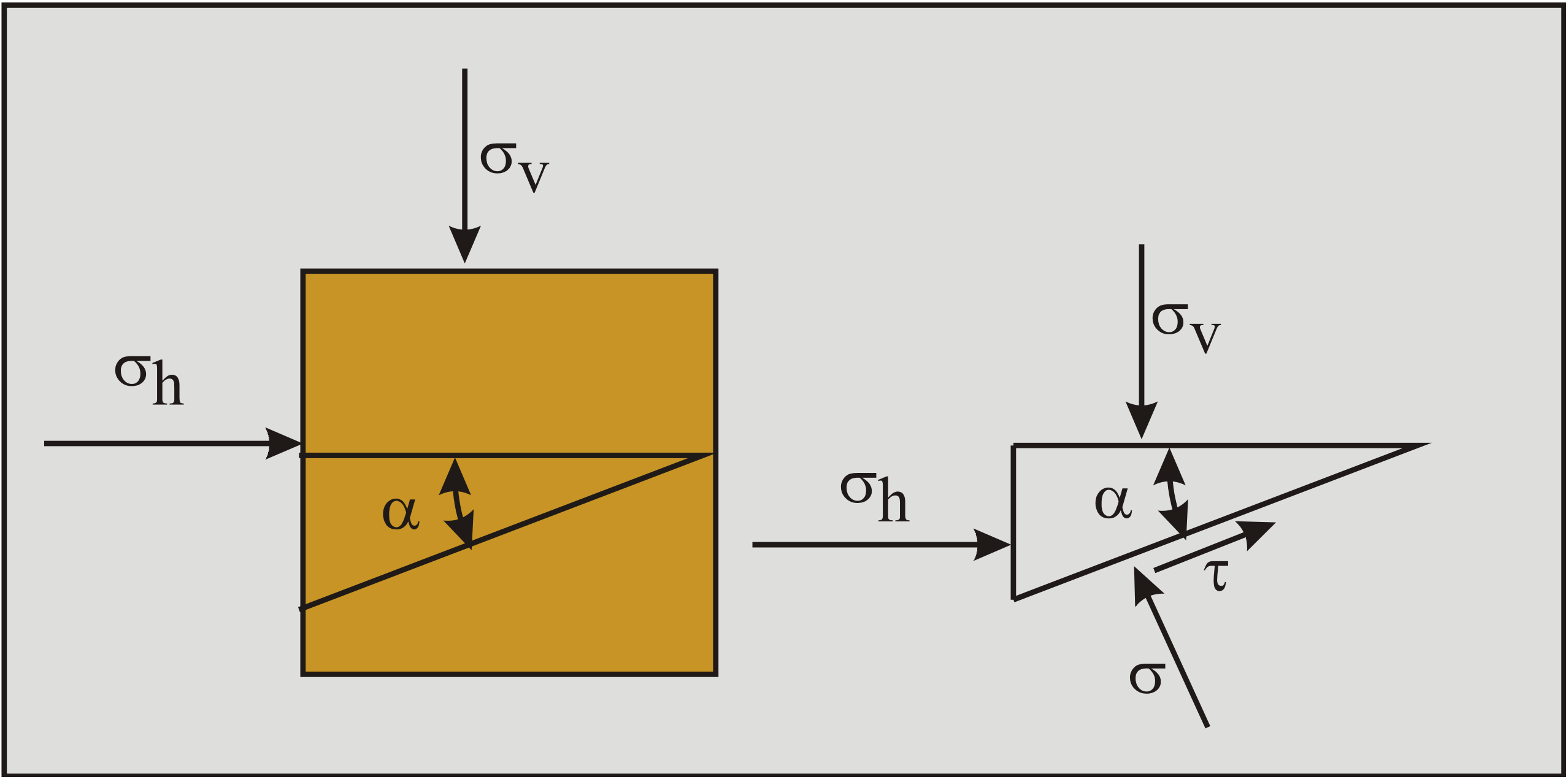
Nyní uvažujme nekonečně malý element tělesa v podmínkách rovinné deformace, jak je znázorněno na obrázku. Na tento element působí svislé napětí \( \sigma_v \) a vodorovné napětí \( \sigma_h \). Na vodorovných a svislých rovinách se předpokládá nulové smykové napětí.
Otázkou je, jaké budou normálové napětí \( \sigma \) a smykové napětí \( \tau \) na rovině, která svírá úhel \( \alpha \) s vodorovným směrem? Pro řešení tohoto problému se odvodí podmínky rovnováhy sil. Rovnováha napětí neexistuje, protože povrchy trojúhelníku na obrázku nejsou stejné.
Pokud je délka povrchu pod úhlem \( \alpha \) považována za 1, pak délka vodorovné strany je \( \cos(\alpha) \) a délka svislé strany \( \sin(\alpha) \). Napětí musí být vynásobena jejich plochou, aby bylo možné získat síly potřebné pro rovnováhu sil (viz obrázek 2-45).
Rovnováha sil#
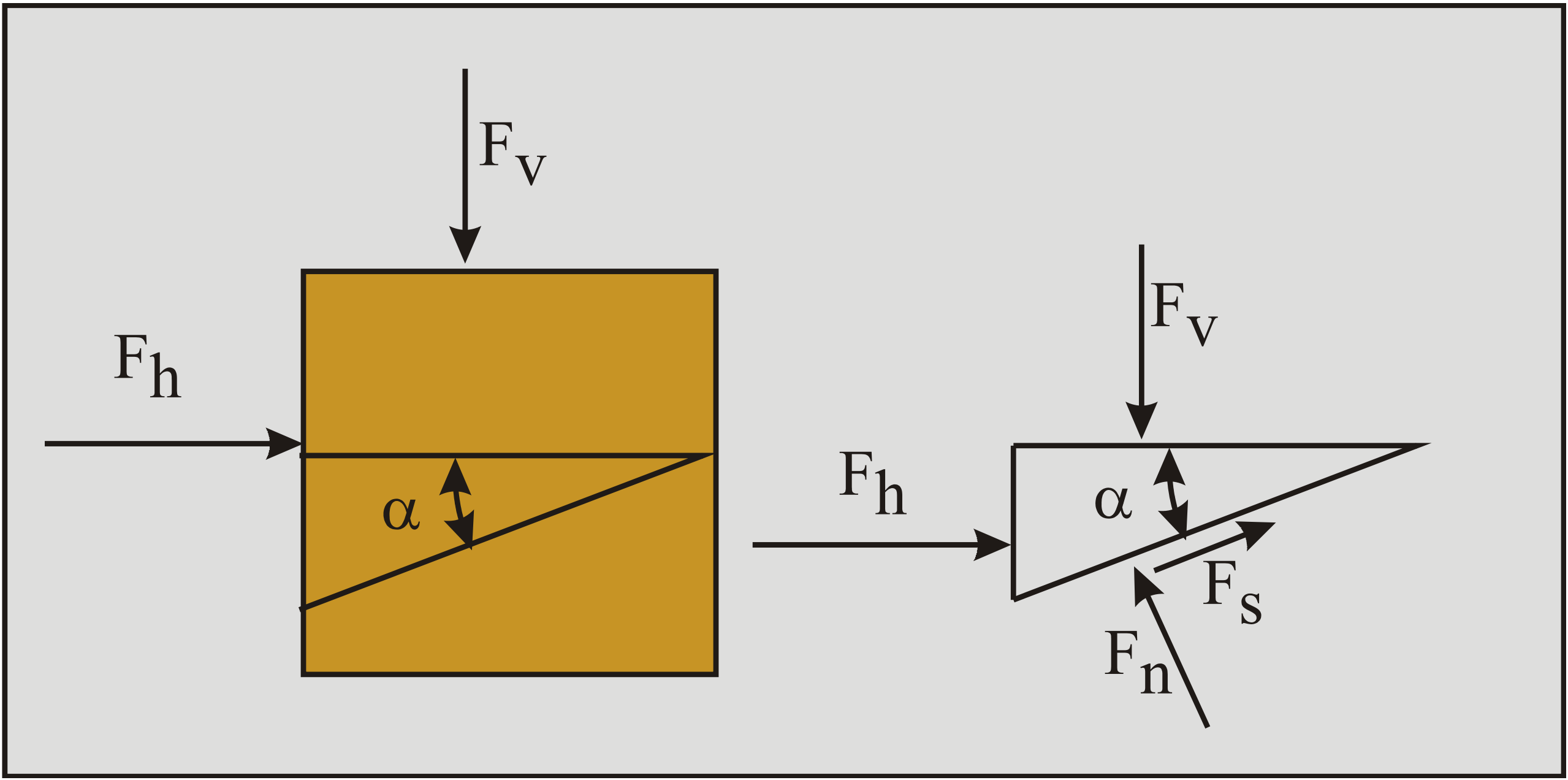
Protože rovnováha napětí neexistuje a existuje pouze rovnováha sil, musí být známy síly působící na element tělesa nebo jejich poměr.
Pro síly platí (za předpokladu délky strany pod úhlem \( \alpha \) rovné 1):
Rovnováha sil ve vodorovném směru:#
Rovnováha sil ve svislém směru:#
Řešení pro normálové napětí \( \sigma \)#
Rovnice se upraví tak, aby eliminovaly smykové napětí \( \tau \). První rovnici vynásobíme \( \sin(\alpha) \) a druhou \( \cos(\alpha) \):
Využijeme vztah z trigonometrie
co můžeme vyjádřit ve tvaru
Sečtením těchto rovnic dojde k eliminaci členů s \( \tau \) a získáme vztah pro \( \sigma \):
Řešení pro smykové napětí \( \tau \)#
První rovnici vynásobíme \( -\cos(\alpha) \) a druhou \( \sin(\alpha) \):
Sečtením rovnic eliminujeme \( \sigma \) a dostaneme:
Rovnice Mohrovy kružnice#
Umocněním předchozích rovnic a jejich sečtením získáme:
Tato rovnice odpovídá obecné rovnici kruhu:
S následujícími hodnotami:
Rovnice Mohrovy kružnice#
Mohrůva kružnice popisuje stav napjatosti v bodě a umožňuje grafickou analýzu napětí v libovolně orientované rovině. Rovnice Mohrovy kružnice pro rovinnou napjatost je:
kde:
\(\sigma_x, \sigma_y\) jsou normálová napětí v hlavních směrech souřadnicového systému,
\(\tau_{xy}\) je smykové napětí v rovině ( xy ),
\(\sigma\) a \(\tau\) jsou normálové a smykové složky napětí na obecné rovině.
Význam Mohrovy kružnice#
Určení hlavních napětí: Hlavní napětí \(\sigma_1\) a \(\sigma_2\) odpovídají průsečíkům kružnice s osou \(\sigma\) a udávají maximální a minimální normálové napětí.
Stanovení maximálního smykového napětí: Maximální smykové napětí \(\tau_{\max}\) odpovídá poloměru kružnice a je určeno vztahem:
\( \tau_{\max} = \frac{\sigma_1 - \sigma_2}{2} \)
Grafická interpretace napětí: Mohrův kruh umožňuje snadno určit hodnoty napětí v libovolně orientované rovině bez nutnosti složitého výpočtu.
Určení orientace hlavních a smykových rovin: Úhel hlavních rovin vzhledem k původní soustavě souřadnic je dán vztahem:
\( \tan 2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y} \)
kde ( \theta_p ) je úhel hlavních napětí vůči ose ( x ).
IFrame('https://www.geogebra.org/classic/DDkrSne2?embed', width='100%', height=800)
def mohr_circle():
# from https://github.com/ProfessorKazarinoff/mohrs_circle/blob/master/mohrs_circle.ipynb
print('PLEASE CONSIDER SIGNS BEFORE ENTERING YOUR VALUES')
stress_x=float(input('Enter the stress in the x-direction: '))
stress_y=float(input('Enter the stress in the y-direction: '))
shear=float(input('Enter the shear: '))
stress_avg=(stress_x+stress_y)/2
stress_max=stress_avg+(((stress_x-stress_y)/2)**2+shear**2)**0.5
stress_min=stress_avg-(((stress_x-stress_y)/2)**2+shear**2)**0.5
R=((((stress_x-stress_y)/2)**2)+shear**2)**0.5 #Also max shear
circle_eqn=((stress_x-stress_avg)**2)-shear**2-R**2
if shear==0:
theta_p=0
theta_s=0
else:
theta_p=0.5*mt.degrees(mt.atan((2*shear)/(stress_x-stress_y)))
if theta_p<=0:
a=-1
else:
a=1
theta_s=a*0.5*mt.degrees(mt.atan((stress_x-stress_y)/(2*shear)))
if abs(stress_min)>abs(stress_max):
maxi=stress_min
mini=stress_max
elif abs(stress_max)>abs(stress_min):
maxi=stress_max
mini=stress_min
#principle planes
shear_lim_p=np.arange(0,0.5*(R+1),1)
shear_lim_n=np.arange(0,-0.5*R-1,-1)
princ_x_slope=(theta_p/abs(theta_p))*mt.tan(mt.radians(theta_p))
princ_y_slope=(theta_p/abs(theta_p))*mt.tan(mt.radians((theta_p+90)))
#princ_x=princ_x_slope*shear_lim+stress_avg
#princ_y=princ_y_slope*shear_lim+stress_avg
if princ_x_slope<0:
range_x=shear_lim_n
princ_x=princ_x_slope*range_x+stress_avg
elif princ_x_slope>0:
range_x=shear_lim_p
princ_x=princ_x_slope*range_x+stress_avg
if princ_y_slope<0:
range_y=shear_lim_n
princ_y=princ_y_slope*range_y+stress_avg
elif princ_y_slope>0:
range_y=shear_lim_p
princ_y=princ_y_slope*range_y+stress_avg
n=100
t=np.linspace(0,2*np.pi,n+1)
x=R*np.cos(t)+stress_avg
y=R*np.sin(t)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.grid(True)
plt.axis('equal')
plt.plot(x,y,'r')
plt.axvline(0,color='black')
plt.axhline(0,color='black')
plt.xlabel('Axial Stress')
plt.ylabel('Shearing Stress')
plt.title('Mohr Circle')
plt.plot(princ_x,range_x,'g',linestyle=':')
plt.plot(princ_y,range_y,'g',linestyle=':')
plt.arrow(stress_avg,0,(stress_x-stress_avg),-shear)
plt.arrow(stress_avg,0,(stress_y-stress_avg),shear)
plt.figure(figsize=[60,40])
ax.annotate('X',
xy=(stress_x,-shear),
arrowprops=dict(facecolor='blue', shrink=0.05))
ax.annotate('Y',
xy=(stress_y,shear),
arrowprops=dict(facecolor='blue', shrink=0.05))
ax.annotate('Max Stress',
xy=(maxi,0),
xytext=(maxi,0.5*shear),
arrowprops=dict(facecolor='blue', shrink=0.05))
ax.annotate('Min Stress',
xy=(mini,0),
xytext=(mini,0.5*shear),
arrowprops=dict(facecolor='blue', shrink=0.05))
plt.show
print(' ')
print(f'Max shear: {np.round(R,3)}')
print(f'Max stress: {np.round(maxi,3)}\nMin stress: {np.round(mini,3)}')
print(f'Average normal stress: {np.round(stress_avg,3)}\n')
print(f'Principal angle: {np.round(theta_p,2)} degrees')
print(f'Principal planes: {np.round(theta_p,2)} degrees and {np.round(theta_p+90,2)} degrees')
print(f'Angle to the shear plane: {np.round(theta_s,2)} degrees')
mohr_circle()
PLEASE CONSIDER SIGNS BEFORE ENTERING YOUR VALUES
---------------------------------------------------------------------------
StdinNotImplementedError Traceback (most recent call last)
/tmp/ipykernel_343469/2115935711.py in <module>
----> 1 mohr_circle()
/tmp/ipykernel_343469/2500666430.py in mohr_circle()
2 # from https://github.com/ProfessorKazarinoff/mohrs_circle/blob/master/mohrs_circle.ipynb
3 print('PLEASE CONSIDER SIGNS BEFORE ENTERING YOUR VALUES')
----> 4 stress_x=float(input('Enter the stress in the x-direction: '))
5 stress_y=float(input('Enter the stress in the y-direction: '))
6 shear=float(input('Enter the shear: '))
~/.local/lib/python3.10/site-packages/ipykernel/kernelbase.py in raw_input(self, prompt)
1279 if not self._allow_stdin:
1280 msg = "raw_input was called, but this frontend does not support input requests."
-> 1281 raise StdinNotImplementedError(msg)
1282 return self._input_request(
1283 str(prompt),
StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.
