2. cvičení

Tuhost

1. Jakou silou je potřeba natáhnout ideální pružinu s konstantou pružiny 120 N/m pro dsažení prodloužení 30 cm?

2. Pružina s tuhostí 600 N/m se používá pro váhu k vážení ryb. Jaká je hmotnost ryby, která by natáhla pružinu o 7,5 cm od její normální délky?

3. Pružina v pogo-sticku je stlačena o 12 cm, když na ní stojí 40 kg vážící dívka. Jaká je tuhost pružiny pro pružinu pogo-stick?

4. Pružina se při působení síly 13 N natáhne o 8,0 cm. Jak daleko se táhne, když působí síla 26 N?

5. Elastická šňůra je dlouhá 80 cm, když na ní visí hmota 10 kg. Po přidání dalších 4,0 kg je šňůra dlouhá 82,5 cm. Jak velká je tuhost šňůry.

6. Pružina s tuhostí 50 N/m visí na stojanu. Druhá pružina s tuhostí 100. N/m visí z první pružiny. Jak daleko se táhnou, pokud je závaží 0,50 kg je zavěšeno na spodní pružině? Jaká je tuhost soustavy pružin? Jak se změní tuhost, když pružiny zavěsíme vedle sebe a jak velkou zátěž přenáší každá z pružin.

Tahový diagram

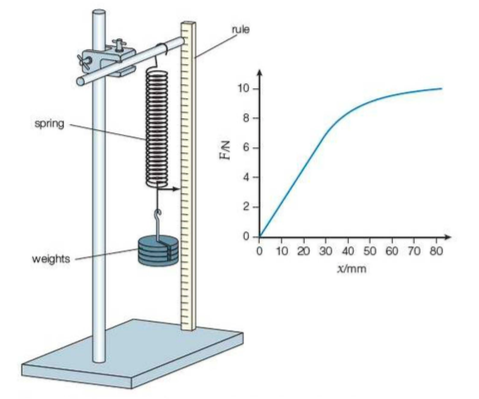
1. Z naměřených dat v experimentu na obrázku určete tuhost pružiny. Vysvětlete průběh naměřené křivky.

   

2. Při zkoušce různých slitin hliníku jsme získali následující smluvný tahový diagram. Popište

   • která slitina vydrží největší napětí

     • do porušení

     • do tvárné deformace

   • která slitina bude mít najvětší prodloužení

   • jak se liší Youngův modul pružnosti mezi slitinami

3. Během tahové zkoušky ocelové tyče o průměru 14 mm byly zaznamenány následující údaje. Měřená délka byla 50 mm.

Zatížení (N)	Prodloužení (mm)
0	0
6310	0.010
12600	0.020
18800	0.030
25100	0.040
31300	0.050
37900	0.060
40100	0.163
41600	0.433
46200	1.25
52400	2.50
58500	4.50
68000	7.50
59000	12.5
67800	15.5
65000	20.0
65500	porušení

Určete:

• mez úmeřnosti

• Youngův modul pružnosti

• mez kluzu

• mez pevnosti

• hodnotu napětí při porušení

Řešení

Napětí a dimenzování

1. Socha o hmotnosti 10 000 N spočívá na vodorovném povrchu na vrcholu 6,0 m vysokého svislého pilíře. Plocha průřezu pilíře je 0,20 m\(^2\) a je vyrobena ze žuly o hustotě 2700 kg/m\(^3\). Najděte tlakové napětí v průřezu umístěném 3,0 m pod vrcholem pilíře a hodnotu tlakového přetvoření (relativního napětí) horního 3,0m segmentu pilíře. Výsledek uveďte včetně znaménka.

Řešení

2. Jakou nejtěžší sochu je možné umístnit na pylon pred Fakultou informačních technologií ČVUT v Dejvicích. Potřebné informace odhadněte nebo dohledejte. Informace o pylonu tady.

3. Navrhněte minimální průměr ocelového prutu, který bude přenášet tahové zatížení 50 kN. Materiál prutu je nízkouhlíková ocel s mezí kluzu 235 MPa a bezpečnostním součinitelem 1,5.

Hooekův zákon

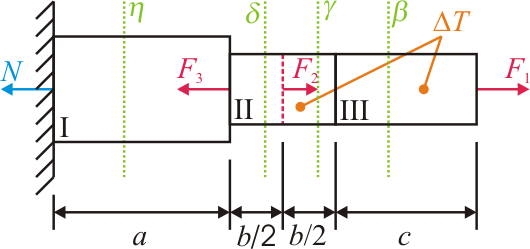
1. Je dán jednostranně vetknutý prut sestavený ze 3 částí o různých rozměrech a mechanických vlastnostech (viz. obrázek dole) zatížený třemi silami \(F_1\), \(F_2\) a \(F_3\) a změnou teploty \(\Delta T\), která působí jen na části II a III.

Parametr	Hodnota	Jednotka
\(F_1\)	25	kN
\(F_2\)	10	kN
\(F_3\)	15	kN
\(\Delta T\)	10	K

Část I - Ocel

Parametr	Hodnota	Jednotka
\(a\)	1	m
\(E_I\)	210	GPa
\(\alpha_I\)	1.0E-5	K⁻¹
\(A_I\)	0.01	m²

Část II - Ocel

Parametr	Hodnota	Jednotka
\(b\)	0.6	m
\(E_{II}\)	210	GPa
\(\alpha_{II}\)	1.0E-5	K⁻¹
\(A_{II}\)	0.0025	m²

Část III - Hliník

Parametr	Hodnota	Jednotka
\(c\)	0.8	m
\(E_{III}\)	70	GPa
\(\alpha_{III}\)	2.3E-5	K⁻¹
\(A_{III}\)	0.0025	m²

• Určete reakční sílu N ve vetknutí.

• Určete velikosti napětí v řezech, které jsou dány rovinami β, γ, δ a η.

• Určete o kolik se prodlouží prut vlivem působení sil a vlivem změny teploty \(\Delta T\).

Kontrola výsledků

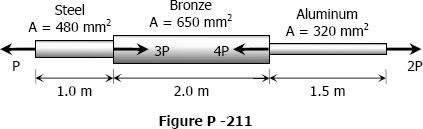
2. Bronzová tyč je upevněna mezi ocelovou tyčí a hliníkovou tyčí, jak je znázorněno na obrázku. V uvedených polohách působí axiální zatížení. Najděte největší hodnotu \(P\), která nepřekročí celkovou deformaci 3,0 mm nebo následující napětí: 140 MPa v oceli, 120 MPa v bronzu a 80 MPa v hliníku. Předpokládejme, že sestava je vhodně vyztužena, aby se zabránilo vybočení. Použijte E\(_\mathrm{ocel}\) = 200 GPa, E\(_\mathrm{hlinik}\) = 70 GPa a E\(_\mathrm{bronz}\) = 83 GPa.

Řešení

Komplexní příklad

1. Důlní šachtový výtah je zavěšen na ocelovém laně o průměru 2,5 cm. Celková hmotnost kabiny a přepravovaných osob je 650 kg. Jak se lano prodlužuje a jaká je hmotnost lana, když

   • v první aproximace zanedbáme hmotnost lana a

     • výtah je na povrchu 12 m pod motorem výtahu?

     • je na dně šachty hluboké 350 m?

   • hmotnost lana nezanedbáme.

Note

Materiálové vlastnosti oceli

Vlastnost	Hodnota
Hustota	7 850 kg/m³
Pevnost v tahu	400 - 550 MPa
Mez kluzu	250 - 350 MPa
Modul pružnosti	200 GPa
Tvrdost (Rockwell)	50 - 80 HRB
Tvrdost (Brinell)	120 - 180 HB
Tvrdost (Vickers)	140 - 190 HV
Tepelná vodivost	45 - 60 W/m·K
Koeficient tepelné roztažnosti	11 - 13 µm/m·K
Elektrická vodivost	6 - 10 MS/m
Bod tavení	1539 °C

2. Jaká je maximální možná hloubka šachty z předešlého příkladu.

3. Jak by mělo vypadat lano, kdyby jsme chtěli dosáhnout vyvrtat šachtu do středu Země.

   1. Uvažujte konstatní gravitační zrychlení.

   2. Uvažujte změnu gravitačního zrychlení s hloubkou šachty.

   3. O kolik se prodlouží lano v důsledku vlastní váhy když dosáhne do středu Země.

   4. O kolik se prodlouží lano v důsledku změny teploty? Je reálné vytvořit takéto lano?

Note

Gravitační zrychlení pod povrchem Země.

Gravitační zrychlení pod povrchem Země je možné odhadnout jako

\[g = \frac{-G M(r)}{r^2} = \frac{- 4 \pi G \rho r}{3} \]

kde \(\rho\) je průměrná hustota Země (\(5500 \) kg/m\(^3\)), \(G\) je gravitační konstanta (6.6743 × 10\(^{-11}\) m\(^3\) kg\(^{-1}\) s\(^{-2}\)) a \(r\) je vzdálenost o středu Země. Pro více informací Shell theorem.

Teplota pod povrchem Země narůstá v tzv. geotermálním gradientu přibližně 25–30 °C/km. Pro přesnější popis se podívejte na geootermální gradient na wikipedii.

• Částečné řešení

• Řešení s vlastní váhou

• Lano stálé pevnosti

Staticky neurčitý problém

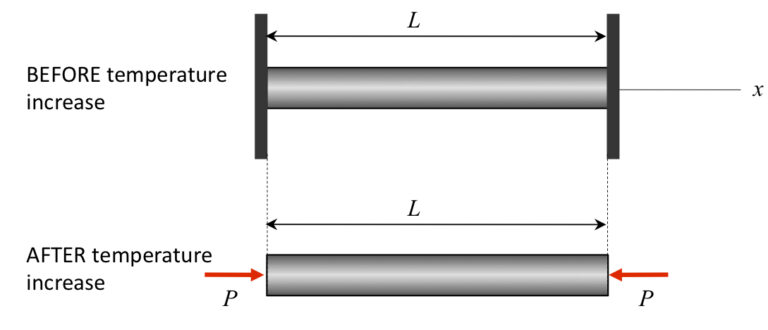
1. Kruhovou ocelovou tyč o délce 1 m a průměru 10 cm vložíme mezi dva pevné podpěry. Jak se změní napětí v tyči když zvýšíme teplotu o 50 K.

Řešení

2. Tyč složená s několika materiálů o různých průřezech je bez pnutí před působením axiálního zatížení \(P_1\) a \(P_2\). Za předpokladu, že stěny jsou tuhé, vypočítejte napětí v každém materiálu, pokud \(P_1\) = 150 kN a \(P_2\) = 90 kN.

Řešení