Konstrukce Mohrovy kružnice

Konstrukce Mohrovy kružnice#

1. Výchozí hodnoty#

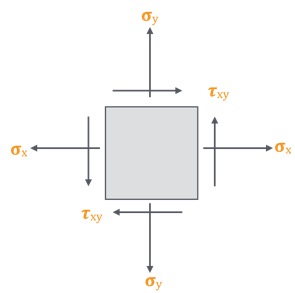
Nejprve se určí základní napěťové složky v daném bodě materiálu:

  • Normálová napětí \( \sigma_x \), \( \sigma_y \)

  • Smykové napětí \( \tau_{xy} \)

https://blog.prepineer.com/wp-content/uploads/2017/10/01-Mohrs-Cricle-Principal-Stresses.jpg

2. Určení bodů na Mohrově kružnici#

  • Bod \( A(\sigma_x, \tau_{xy}) \) odpovídá napětí na rovině s normálou ve směru osy \( x \).

  • Bod \( B(\sigma_y, -\tau_{xy}) \) odpovídá napětí na rovině s normálou ve směru osy \( y \).

https://blog.prepineer.com/wp-content/uploads/2017/10/02-mohrs-circle-guidelines-shear-strearing-stresses.png

Smykové napětí vynášíme do Mohrova diagramu jako kladné jestliže vnější normála \(\vec{n}\) splyne s tímto napětím ve smyslu hodinových ručiček.

Body A, B, leží na Mohrově kružnici.

https://blog.prepineer.com/wp-content/uploads/2017/10/04-Mohrs-circle-guidelines-plot-magnitude-of-couple.png

3. Konstrukce kružnice#

  1. Bod \( A \) a bod \( B \) spojíme úsečkou.

  2. Na ose \( \sigma \) označíme bod \( C \) jako průsečník úsečky AB s osou \(\sigma\).

https://blog.prepineer.com/wp-content/uploads/2017/10/05-Mohrs-circle-guidelines-center-of-the-Mohr%E2%80%99s-circle-is-obtained-graphically-by-plotting-the-two-points-representing-the-two-known-states-of-stress.png

  1. Vykreslíme kružnici se středem \( C \) a poloměrem \(CA\).

https://blog.prepineer.com/wp-content/uploads/2017/10/06-Mohrs-circle-guidelines-6.-Draw-the-Mohr%E2%80%99s-circle-assuming-the-connection-line-as-the-diameter-of-the-circle.png

4. Určení hlavních napětí#

Hlavní napětí \( \sigma_1, \sigma_2 \) odpovídají průsečíkům kružnice s osou \( \sigma \):

\[ \sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm R \]

7. Maximální smykové napětí#

Maximální smykové napětí odpovídá hornímu a dolnímu bodu Mohrovy kružnice:

\[ \tau_{\max} = R \]
https://blog.prepineer.com/wp-content/uploads/2017/10/07-Mohrs-circle-construction-guidelines-Stress-Analysis-on-Mohr-circle-To-get-normal-and-shear-stress-values-at-any-plane-theta.png

8. Určení hlavních a smykových rovin#

Úhel hlavních napěťových rovin vzhledem k původní soustavě souřadnic je dán vztahem:

\[ \tan 2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y} \]

Úhel mezi osou \( x \) a rovinou maximálního smykového napětí je:

\[ \theta_s = \theta_p + 45^\circ \]

Numerické určení středu kružnice**#

Střed Mohrovy kružnice \( S \) má souřadnice:

\[ S = \left( \frac{\sigma_x + \sigma_y}{2}, 0 \right) \]

Numerické určení poloměru kružnice**#

Poloměr \( R \) kružnice je dán vztahem:

\[ R = \sqrt{\left( \frac{\sigma_x - \sigma_y}{2} \right)^2 + \tau_{xy}^2} \]

Rovnice Mohrovy kružnice**#

Mohrova kružnice je popsána rovnicí:

\[ \left( \sigma - \frac{\sigma_x + \sigma_y}{2} \right)^2 + \tau^2 = R^2 \]