Skalár a vektor

připraveno na základě podkladů Marcos Duarte, Renato Naville Watanabe, Laboratory of Biomechanics and Motor Control

Python velmi dobře zpracovává všechny matematické operace s číselnými skaláry a vektory a pro podobné věci můžete použít Sympy, ale s abstraktními symboly. Podívejme se stručně skaláry a vektory a ukážeme, jak používat Python pro numerický výpočet.

Přehled o skalárech a vektorech viz kapitola 2 Andy Ruina and Rudra Pratap: Introduction to Statics and Dynamics.

Nastavení Pythonu

from IPython.display import IFrame
import math
import numpy as np

Skalární veličina

Skalární veličina je fyzikální veličina, která je plně určena jediným číselným údajem a jednotkou. To znamená, že k jejímu popisu stačí uvést, jaká je její velikost. Na rozdíl od vektorových veličin, které mají kromě velikosti také směr, skaláry nemají žádné směrové vlastnosti.

Příklady skalárních veličin:

• Délka: Například délka tužky je 15 cm.

• Hmotnost: Hmotnost knihy je 500 gramů.

• Čas: Doba trvání filmu je 2 hodiny.

• Teplota: Teplota vody je 20 stupňů Celsia.

• Energie: Kinetická energie pohybujícího se tělesa je 100 Joule.

Grafické znázornění skalárů Skaláry se obvykle graficky znázorňují pouze jako čísla s příslušnou jednotkou. Na rozdíl od vektorů, které se znázorňují jako úsečky s orientací, skaláry nemají žádný směr, a proto je jejich grafické znázornění jednoduché.

Skalární operace v Pythonu

Jednoduché aritmetické operace se skaláry jsou skutečně jednoduché:

a = 2
b = 5
print('a =', a, ', b =', b)
print('a + b =', a + b)
print('a - b =', a - b)
print('a * b =', a * b)
print('a / b =', a / b)
print('a ** b =', a ** b)
print('sqrt(b) =', math.sqrt(b))

a = 2 , b = 5
a + b = 7
a - b = -3
a * b = 10
a / b = 0.4
a ** b = 32
sqrt(b) = 2.23606797749979

Pokud máte sadu čísel nebo pole, je pravděpodobně lepší použít NUMPY; Bude to rychlejší pro velké soubory dat a v kombinaci se Scipy, má mnohem více matematických funkcí.

a = 2
b = [3, 4, 5, 6, 7, 8]
b = np.array(b)
print('a =', a, ', b =', b)
print('a + b =', a + b)
print('a - b =', a - b)
print('a * b =', a * b)
print('a / b =', a / b)
print('a ** b =', a ** b)
print('np.sqrt(b) =', np.sqrt(b))  # Použijte funkce numpy pro numpy pole

a = 2 , b = [3 4 5 6 7 8]
a + b = [ 5  6  7  8  9 10]
a - b = [-1 -2 -3 -4 -5 -6]
a * b = [ 6  8 10 12 14 16]
a / b = [0.66666667 0.5        0.4        0.33333333 0.28571429 0.25      ]
a ** b = [  8  16  32  64 128 256]
np.sqrt(b) = [1.73205081 2.         2.23606798 2.44948974 2.64575131 2.82842712]

Numpy provádí aritmetické operace jediného čísla v a se všemi čísly pole b. Tomu se říká v informatice pojmem broadcasting. I když máte dvě pole (ale musí mít stejnou velikost), Numpy pravidla platí pro vás:

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print('a =', a, ', b =', b)
print('a + b =', a + b)
print('a - b =', a - b)
print('a * b =', a * b)
print('a / b =', a / b)
print('a ** b =', a ** b)

a = [1 2 3] , b = [4 5 6]
a + b = [5 7 9]
a - b = [-3 -3 -3]
a * b = [ 4 10 18]
a / b = [0.25 0.4  0.5 ]
a ** b = [  1  32 729]

Extenzivní a intenzivní veličiny

V termodynamice a fyzice obecně rozlišujeme dva základní typy veličin: extenzivní a intenzivní. Toto rozdělení je důležité pro pochopení chování systémů a jejich vlastností.

Extenzivní veličiny

• Definice: Extenzivní veličiny jsou takové, jejichž hodnota závisí na velikosti systému, tedy na množství látky nebo hmotnosti. Pokud zdvojnásobíme množství látky v systému, zdvojnásobí se i hodnota extenzivní veličiny.

• Příklady:

  • Hmotnost (m): Celková hmotnost tělesa.

  • Objem (V): Prostor, který těleso zabírá.

  • Energie (E): Celková energie systému (vnitřní energie, kinetická energie, potenciální energie).

  • Entropie (S): Míra neuspořádanosti systému.

  • Náboj (Q): Celkový elektrický náboj.

  • Délka (l): Rozměr tělesa.

Intenzivní veličiny

• Definice: Intenzivní veličiny jsou takové, jejichž hodnota nezávisí na velikosti systému. Zůstávají stejné, i když změníme množství látky v systému.

• Příklady:

  • Teplota (T): Míra horkosti nebo chladu.

  • Tlak (p): Síla působící na jednotku plochy.

  • Hustota (ρ): Hmotnost na jednotku objemu.

  • Měrná tepelná kapacita (c): Množství tepla potřebné k ohřátí jednotky hmotnosti o 1 stupeň.

  • Koncentrace (c): Množství látky v daném objemu.

Vztah mezi extenzivními a intenzivními veličinami

• Poměr dvou extenzivních veličin dává často intenzivní veličinu (např. hustota = hmotnost/objem).

• Intenzivní veličiny jsou “kvalitativní” vlastnosti, zatímco extenzivní veličiny jsou “kvantitativní”.

Praktický význam

Rozlišení mezi extenzivními a intenzivními veličinami je klíčové pro správné pochopení a popis termodynamických systémů a procesů. Umožňuje nám například:

• Vytvářet termodynamické modely a rovnice.

• Porovnávat vlastnosti různých látek.

• Předpovídat chování systémů při změnách podmínek.

Vektor

Vektorová veličina je fyzikální veličina, která je charakterizována nejen svou velikostí, ale také směrem.

Co to znamená?

Velikost: Určuje “intenzitu” nebo “množství” této veličiny. Například rychlost 50 km/h udává velikost rychlosti. Směr: Určuje, kam veličina “směřuje” nebo “působí”. Například rychlost 50 km/h na východ udává jak velikost, tak i směr pohybu. Grafické znázornění:

Vektor se graficky znázorňuje jako orientovaná úsečka.

Délka úsečky představuje velikost vektoru. Směr úsečky (a šipka na jejím konci) představuje směr vektoru.

Symboly pro vektory jsou obvykle v knihách tištěny tučně, jako a. Mezi další zvyklosti označování patří \(\vec {a}\). Aby jsme předešli nedorozumění budeme v našem kurzu označovat vektory \(\vec{\mathbf{a}}\).

Například zvažte polohu bodu v prostoru představovaném vektorem:

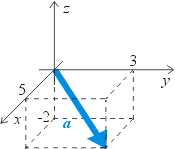
Pozice bodu představovaného vektorem v karteziánském souřadném systému.

Poloha bodu (vektor) výše může být reprezentována jako n -tice hodnot:

\[ (x,\: y,\: z) \; \Rightarrow \; (5, 3, -2) \]

nebo ve formě matice:

\[\begin{split} \begin{bmatrix} x \\y \\z \end{bmatrix} \;\; \Rightarrow \;\; \begin{bmatrix} 1 \\3 \\2 \end{bmatrix}\end{split}\]

Můžeme použít pole Numpy k reprezentaci komponent vektorů. Například pro výše uvedený vektor je vyjádřen v Pythonu jako:

a = np.array([1, 3, 2])
print('a =', a)

a = [1 3 2]

Vektor může být také reprezentován jako: $\( \overrightarrow{\mathbf{a}} = a_x\hat{\mathbf{i}} + a_y\hat{\mathbf{j}} + a_z\hat{\mathbf{k}} \)$

kde vektory \( \vec{\mathbf{i}}, \, \vec{\mathbf{j}}, \, \vec{\mathbf{k}} \, \) jsou jednotkové vektory ve směru jednotlivých souřadnicových os a jsou obvykle reprezentovány v barevné sekvenci rgb (červená, zelená, modrá) pro snadnější vizualizaci. Násobek \(a_x \vec{\mathbf{i}}, \: a_y \vec{\mathbf{j}}, \: a_z \vec{\mathbf{k}} \) jsou vektorové komponenty vektoru \(\vec{\mathbf{a}}\) .

Jednotkový vektor (můžete se setkat také s označením verzor) je vektor, jehož délka (nebo norma) je 1.

IFrame('https://www.geogebra.org/classic/ydu8a7t7?embed', width='100%', height=500)

Násobení vektoru skalárem

U složek vektoru \({a_x}\vec{\mathbf{i}}\) jsme již využili násobení vektoru \(\vec{\mathbf{i}}\) číslem \(a_x\).

Násobení vektoru skalárem je operace, která mění velikost vektoru, ale ne jeho směr. Můžeme si to představit jako “natažení” nebo “zkrácení” vektoru.

Jak to funguje:

• Zvětšení: Když násobíme vektor kladným skalárem (číslem větším než 1), zvětšíme jeho velikost. Je to jako bychom vektor “natahovali”.

• Zmenšení: Když násobíme vektor kladným skalárem mezi 0 a 1, zmenšíme jeho velikost. Je to jako bychom vektor “zkracovali”.

• Změna směru: Když násobíme vektor záporným skalárem, změníme jeho směr na opačný. Je to jako bychom vektor “otočili” o 180 stupňů. Velikost vektoru se přitom může také změnit v závislosti na absolutní hodnotě skaláru.

a = np.array([2,1])
b = 2
c = 0.5
d = -1
print('a * b =', a* b)
print('a * b =', a * c)
print('a * d =', a * d)

a * b = [4 2]
a * b = [1.  0.5]
a * d = [-2 -1]

IFrame('https://www.geogebra.org/classic/HYZXHadK?embed', width='100%', height=500)

Jestliže máme vektor \(\vec{{\mathbf{a}}}\), existuje k němu opačný vektor \(-\vec{{\mathbf{a}}}\). Pro tento vektor platí: $\(\vec{{\mathbf{a}}} + (-\vec{{\mathbf{a}}}) = \vec{{\mathbf{0}}}\)\( kde \)\vec}\( je nulový vektor \)\vec} = (0,0,0)$.

Násobení skalárem funguje v Pythonu jednoduše jako násobení pole. Protože však nyní jednáme s vektory, nyní některé operace nedávají smysl. Například pro dvojici vektorů neexistují žádné násobení, dělení, síla a druhou odmocninu ve způsobu, jakým jsme vypočítali.

Jednotkový vektor \(\vec{\mathbf{u}}\) nenulového vektoru \(\vec{\mathbf{a}}\) je jednotkový vektor se stejným směrem:

\[ \mathbf{\vec{u}} = \frac{\overrightarrow{\mathbf{a}}}{||\overrightarrow{\mathbf{a}}||} = \frac{a_x\,\hat{\mathbf{i}} + a_y\,\vec{\mathbf{j}} + a_z\, \vec{\mathbf{k}}}{\sqrt{a_x^2+a_y^2+a_z^2}} \]

Velikost (délka nebo norma) vektoru

Velikost (délka) vektoru je často reprezentována symbolem \( || \; || \), také známou jako norma (nebo euklidovská norma) vektoru a je definována jako: $\( ||\overrightarrow{\mathbf{a}}|| = \sqrt{a_x^2+a_y^2+a_z^2} \)$ Funkce numpy.linalg.norm počítá normu:

a = np.array([1, 2, 3])
np.linalg.norm(a)

3.7416573867739413

Nebo můžeme definici použít přímo a spočítat:

np.sqrt(np.sum(a*a))

3.7416573867739413

Poté, verzor (jedotkový vektor) pro vektor \( \overrightarrow{\mathbf{a}} = (1, 2, 3)\) je:

a = np.array([1, 2, 3])
u = a/np.linalg.norm(a)
print('u =', u)

u = [0.26726124 0.53452248 0.80178373]

A můžeme ověřit, že jeho velikost je skutečně 1:

np.linalg.norm(u)

1.0

Ale reprezentace vektoru jako n-tice hodnot je platná pouze pro vektor s jeho působištěm, který se shoduje s počátkem souřadnicového systému \( (0, 0, 0) \). Například zvažte následující vektor:

Takový vektor nelze reprezentovat \((B_x, B_y, B_z)\), protože by to bylo pro vektor od původu do bodu B., aby přesně reprezentoval tento vektor, který potřebujeme dva vektory \(\vec{OB}\) a \(\vec{OA}\). Tato skutečnost je důležitá, když provádíme některé výpočty v mechanice.

Sčítání a odečítání vektorů

Sčítáním dvou vektorů získáme další vektor: $\( \overrightarrow{\mathbf{a}} + \overrightarrow{\mathbf{b}} = (a_x\vec{\mathbf{i}} + a_y\vec{\mathbf{j}} + a_z\vec{\mathbf{k}}) + (b_x\vec{\mathbf{i}} + b_y\vec{\mathbf{j}} + b_z\vec{\mathbf{k}}) = (a_x+b_x)\vec{\mathbf{i}} + (a_y+b_y)\vec{\mathbf{j}} + (a_z+b_z)\vec{\mathbf{k}} \)$

V maticovém zápisu to bude vypadat: $\(\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} + \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = \begin{bmatrix} a_x + b_x \\ a_y + b_y \\ a_z + b_z \end{bmatrix}\)$

Metoda rovnoběžníku je grafická metoda, která nám umožňuje názorně sčítat dva vektory.

Postup:

1. Nakreslení vektorů: Oba vektory, které chceme sčítat, nakreslíme tak, aby jejich počáteční body splývaly.

2. Sestrojení rovnoběžníku: Z koncových bodů obou vektorů sestrojíme rovnoběžníky. Tj. z koncového bodu prvního vektoru sestrojíme přímku rovnoběžnou s druhým vektorem a naopak. Tím vznikne rovnoběžník.

3. Výsledný vektor: Úhlopříčka rovnoběžníku, která vychází z bodu, kde se oba vektory setkávají, představuje výsledný vektor (vektorový součet).

IFrame('https://www.geogebra.org/classic/FCknj7c3?embed', width='100%', height=500)

V prostoru metoda rovnoběžníku funguje stejně, ale musíme jeho konstrukci provést v rovině určené oběma vektory. Proto se v prostoru raděi spoléháme na výpočet

IFrame('https://www.geogebra.org/classic/gkhaxb2b?embed', width='100%', height=500)

Odčítání dvou vektorů je také dalším vektorem:

\[ \overrightarrow{\mathbf{a}} - \overrightarrow{\mathbf{b}} = (a_x\vec{\mathbf{i}} + a_y\vec{\mathbf{j}} + a_z\vec{\mathbf{k}}) - (b_x\vec{\mathbf{i}} + b_y\vec{\mathbf{j}} + b_z\vec{\mathbf{k}}) = (a_x-b_x)\vec{\mathbf{i}} + (a_y-b_y)\vec{\mathbf{j}} + (a_z-b_z)\vec{\mathbf{k}} \]

V maticovém zápisu to bude vypadat: $\(\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} - \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = \begin{bmatrix} a_x - b_x \\ a_y - b_y \\ a_z - b_z \end{bmatrix}\)$

Zvažte dvě 2D pole (řádky a sloupce) představující polohu dvou objektů pohybujících se v prostoru. Sloupce představují vektorové komponenty a řádky hodnot polohového vektoru v různých okamžicích. Je snadné provést sčítání a odčítání s těmito vektory:

a = np.array([[1, 2, 3], [1, 1, 1]])
b = np.array([[4, 5, 6], [7, 8, 9]])
print('a =', a, '\nb =', b)
print('a + b =', a + b)
print('a - b =', a - b)

a = [[1 2 3]
 [1 1 1]] 
b = [[4 5 6]
 [7 8 9]]
a + b = [[ 5  7  9]
 [ 8  9 10]]
a - b = [[-3 -3 -3]
 [-6 -7 -8]]

Numpy zvládne n-dimenzionální pole s velikostí omezenou dostupnou pamětí v počítači.

A můžeme provádět operace na každém vektoru, například vypočítat normu každého z nich. Nejprve zkontrolujeme tvar proměnné a pomocí metody„ tvar “nebo funkce numpy.shape:

print(a.shape)
print(np.shape(a))

(2, 3)
(2, 3)

To znamená, že proměnná A má 2 řádky a 3 sloupce. Musíme sdělit funkci numpy.norm pro výpočet normy pro každý vektor, tj. Abychom fungovali skrz sloupce proměnné a pomocí paraneter osy:

np.linalg.norm(a, axis=1)

array([3.74165739, 1.73205081])

Vektor mezi dvěma danými body

podle Lesson Explainer: Vectors in Space

Začněme uvažováním dvou odlišných bodů a v prostoru, jak je znázorněno na obrázku.

Chceme sestrojit vektor z \(A\) do \(B\), který je označen \(\vec{AB}\)

Abychom toho dosáhli, můžeme cestovat přes počátek, jak je znázorněno na obrázku níže. Můžeme jít z bodu \(O\) do bodu \(A\) a pak z bodu \(O\) do bodu \(B\).

To lze zapsat jako následující rovnici pomocí vektorů: $\(\vec{AB} = \vec{AO} + \vec{OB} \)\( Pro jakýkoli bod \)A\( platí \)\(\vec{AO} = - \vec{OA}\)\( Tuto vlastnost můžeme použít k přepsání naší rovnice takto: \)\(\vec{AB} = -\vec{OA} + \vec{BO} \)\( Vektor \)\vec{AB}$ je tak možné vyjádřit

$\(\vec{AB} = \vec{BO} - \vec{OA} = \vec{\mathbf{B}} - \vec{\mathbf{A}}\)$
Vektor mezi dvěma body můžeme získat tak, že od polohového vektoru konečného bodu odčítáme polohový vektor počátečního bodu.

IFrame('https://www.geogebra.org/classic/NrzgxrQa?embed', width='100%', height=500)

Skalární součin

Skalární součin je operace, která přiřazuje dvěma vektorům jediné číslo (skalár).

Toto číslo nám poskytuje informaci o tom, jak moc jsou tyto dva vektory “souhlasné” neboli jak moc “směřují stejným směrem”. Skalární součin umožňuje vypočítat projekci jednoho vektoru na druhý. Tato projekce nám říká, jak velká část jednoho vektoru “směřuje” ve směru druhého vektoru.

Matematický zápis Skalární součin vektorů \(\vec{\mathbf{u}}\) a \(\vec{\mathbf{v}}\) se značí \(\vec{\mathbf{u}} \cdot \vec{\mathbf{u}}\).

Definujme skalární součin jednotkových vektorů v pravoúhlém souřadnicovém systému. $\( \vec{\mathbf{i}} \cdot \vec{\mathbf{i}} = \vec{\mathbf{j}} \cdot \vec{\mathbf{j}} = \vec{\mathbf{k}} \cdot \vec{\mathbf{k}}= 1 \quad \text{a} \quad \vec{\mathbf{i}} \cdot \vec{\mathbf{j}} = \vec{\mathbf{i}} \cdot \vec{\mathbf{k}} = \vec{\mathbf{j}} \cdot \vec{\mathbf{k}} = 0 \)$

PSkalární součin mezi dvěma vektory je matematická operace algebraicky definovaná jako součet násobků jednotlivých složek (v každém směru) obou vektorů. $\( \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} = (a_x\,\vec{\mathbf{i}}+a_y\,\vec{\mathbf{j}}+a_z\,\vec{\mathbf{k}}) \cdot (b_x\,\vec{\mathbf{i}}+b_y\,\vec{\mathbf{j}}+b_z\,\vec{\mathbf{k}}) = a_x b_x + a_y b_y + a_z b_z \)$

Geometrický ekvivalent skalární součinu je násobek velikostí dvou vektorů a kosinunu úhlu mezi nimi: $\( \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} = ||\overrightarrow{\mathbf{a}}||\:||\overrightarrow{\mathbf{b}}||\:cos(\theta) \)$

Což je také ekvivalentní tomu, že skalární součin vektoru \(\overrightarrow{\mathbf{a}}\) and \(\overrightarrow{\mathbf{b}}\) je velikostí vektoru \(\overrightarrow{\mathbf{a}}\) a velikostí složky \(\overrightarrow{\mathbf{b}}\) paralelní s \(\overrightarrow{\mathbf{a}}\)

V maticovém zápisu můžeme zapsat jako násobení dvojice vektorů $\( \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} = \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix}^T = \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} [b_x, b_y, b_z]\)$

V této interaktivní animaci lze vizualizovat skalární součin mezi dvěma vektory:

IFrame('https://www.geogebra.org/classic/ncdf2jsw?embed',
       width='100%', height=500)

Numpy funkce pro skalární součin je numpy.dot:

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print('a =', a, '\nb =', b)
print('np.dot(a, b) =', np.dot(a, b))

a = [1 2 3] 
b = [4 5 6]
np.dot(a, b) = 32

Nebo můžeme definici použít přímo a spočítat přímo:

np.sum(a*b)

32

Pro 2D pole vykonává funkce numpy.dot spíše násobení než skalárního součinu; Pojďme tedy použít funkci numpy.sum:

a = np.array([[1, 2, 3], [1, 1, 1]])
b = np.array([[4, 5, 6], [7, 8, 9]])
np.sum(a*b, axis=1)

array([32, 24])

Vektorový součin

Vektorový součin je binární operace definovaná ve třírozměrném euklidovském prostoru, která přiřadí dvěma vektorům nový vektor, který je na ně oba kolmý. Na rozdíl od skalárního součinu, jehož výsledkem je číslo (skalár), výsledkem vektorového součinu je opět vektor.

Matematický zápis Vektorový součin vektorů \(\vec{\mathbf{a}}\) a \(\vec{\mathbf{b}}\) se značí \(\vec{\mathbf{a}} \times \vec{\mathbf{b}}\).

Geometrická interpretace

• Směr: Výsledný vektor je kolmý k rovině určené vektory \(\vec{\mathbf{a}}\) a \(\vec{\mathbf{b}}\). Jeho směr se určuje pomocí pravidla pravé ruky: Pokud prsty pravé ruky ohneme od vektoru u k vektoru v, ukazuje nám palec směr výsledného vektoru.

• Velikost: Velikost výsledného vektoru je rovna ploše rovnoběžníku určeného vektory \(\vec{\mathbf{a}}\) a \(\vec{\mathbf{b}}\).

  \[ \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}} = ||\overrightarrow{\mathbf{a}}||\:||\overrightarrow{\mathbf{b}}||\:sin(\theta) \]

Obr. Plocha rovnoběžníku je rovna velikosti vektorového součinu(zdroj Wikipedia).

Analytické vyjádření

Definujme vektorový součin jednotkových vektorů: $\( \begin{array}{l l} \vec{\mathbf{i}} \times \vec{\mathbf{i}} = \vec{\mathbf{j}} \times \vec{\mathbf{j}} = \vec{\mathbf{k}} \times \vec{\mathbf{k}} = 0 \\ \vec{\mathbf{i}} \times \vec{\mathbf{j}} = \vec{\mathbf{k}}, \quad \vec{\mathbf{k}} \times \vec{\mathbf{k}} = \vec{\mathbf{i}}, \quad \vec{\mathbf{k}} \times \vec{\mathbf{i}} = \vec{\mathbf{j}} \\ \vec{\mathbf{j}} \times \vec{\mathbf{i}} = -\vec{\mathbf{k}}, \quad \vec{\mathbf{k}} \times \vec{\mathbf{j}}= -\vec{\mathbf{i}}, \quad \vec{\mathbf{i}} \times \vec{\mathbf{k}} = -\vec{\mathbf{j}} \end{array} \)$

získáme pak

\[ \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}} = (a_x\,\vec{\mathbf{i}} + a_y\,\vec{\mathbf{j}} + a_z\,\vec{\mathbf{k}}) \times (b_x\,\vec{\mathbf{i}}+b_y\,\vec{\mathbf{j}}+b_z\,\vec{\mathbf{k}}) = (a_y b_z-a_z b_y)\vec{\mathbf{i}} + (a_z b_x-a_x b_z)\vec{\mathbf{j}}+(a_x b_y- a_y b_x)\vec{\mathbf{k}} \]

Vektorový součin lze také vypočítat jako determinant matice: $\( \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}} = \left| \begin{array}{ccc} \vec{\mathbf{i}} & \vec{\mathbf{j}} & \vec{\mathbf{k}} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{array} \right| = a_y b_z \vec{\mathbf{i}} + a_z b_x \vec{\mathbf{j}} + a_x b_y \vec{\mathbf{k}} - a_y b_x \vec{\mathbf{k}}-a_z b_y \vec{\mathbf{i}} - a_x b_z \vec{\mathbf{j}} \)\( \)\(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}} = (a_y b_z-a_z b_y)\vec{\mathbf{i}} + (a_z b_x-a_x b_z)\vec{\mathbf{j}} + (a_x b_y-a_y b_x)\vec{\mathbf{k}} \)$

V této interaktivní animaci lze vizualizovat vektorový součin mezi dvěma vektory:

IFrame('https://www.geogebra.org/classic/cz6v2U99?embed',
       width='100%', height=500)

Numpy funkce pro křížový produkt je numpy.cross:

a = [0, 0, 5]
b = [3, 0, 0]

print('a =', a, '\n b =', b)
print('np.cross(a, b) =', np.cross(a, b))

a = [0, 0, 5] 
 b = [3, 0, 0]
np.cross(a, b) = [ 0 15  0]

Pro 2D pole s vektory v různých řádcích:

a = np.array([[1, 2, 3], [1, 1, 1]])
b = np.array([[4, 5, 6], [7, 8, 9]])
np.cross(a, b, axis=1)

array([[-3,  6, -3],
       [ 1, -2,  1]])

a = np.array([1, 2, 0])
b = np.array([0, 1, 3])
c = np.array([1, 0, 1])

Další čtení

• Přečtěte si stránky 44-92 první kapitoly Ruina and Rudra’s book o skalárech a vektorech v mechanice.

Video přednášky na internetu

• Khan Academy: Vectors

• Vectors, what even are they?

• Základy vektorové a tenzorové algebry

Problémy

1. Vzhledem k vektorům, \(\overrightarrow{\mathbf{a}}=[1, 0, 0]\) a \(\overrightarrow{\mathbf{b}}=[1, 1, 1]\), vypočítejte jejich skalární a vektorový součin.

2. Vypočítejte jednotkové vektory pro \( [2, −2, 3] \) a \( [3, −3, 2] \) a určete ortogonální vektor těchto dvou vektorů.

3. Vzhledem k vektorům \(a = [1, 0, 0]\) a \(b = [1, 1, 1]\), vypočítejte \(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}\) a ověřte, že tento vektor je ortogonální na původní vektory. Vypočítejte také \(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{a}}\) a porovnejte s \(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}\).

4. Vzhledem k vektorům \( [1, 1, 0]; [1, 0, 1]; [0, 1, 1] \), vypočítejte ortonormální bázi souřadnicového systému.

5. Vyřešte úlohy 1.1 až 1.9, 1.11 (pomocí Pythonu), 1.12, 1.14, 1.17, 1.18 do 1.24 knihy Ruiny a Rudry

6. Z knihy Ruiny a Rudry vyřešte problémy 1.1.1 do 1.3.16.

Pokud si nejste jisti ve skalárech a vektorech, měli byste tyto problémy vyřešit nejprve ručně a poté pomocí Pythonu zkontrolovat odpovědi.Znalost vektorového počtu je nezbytná pro další zvládnutí mechaniky.

Reference

• Ruina A, Rudra P (2019) Introduction to Statics and Dynamics. Oxford University Press.