Souřadnicové systémy#
Pohyb (změna polohy v prostoru v závislosti na čase) není absolutní pojem; je potřeba referenční bod, vůči kterému popisujeme pohyb objektu. Stejně tak stav této reference nemůže být absolutní v prostoru, a proto je pohyb relativní.
Referenční soustava je místo, vzhledem k němuž si volíme popis pohybu objektu. V této referenční soustavě definujeme soustavu souřadnic (soubor os), ve které měříme pohyb objektu (ale pojmy referenční soustava a soustava souřadnic se často používají zaměnitelně).
Volba referenční soustavy a souřadného systému je často věcí úsudku a praktičnosti. Existuje však důležitý rozdíl mezi referenčními soustavami, když se zabýváme dynamikou pohybu, kde nás zajímají síly související s pohybem objektu. V dynamice hovoříme o inerciální soustavě (také známé jako Galileova soustava), když Newtonovy pohybové zákony v jejich jednoduché formě v této soustavě platí, a o neinerciální soustavě (také známé jako neinerciální referenční soustava), když Newtonovy zákony v jejich jednoduché formě neplatí (v takové soustavě se objevují zdánlivé zrychlení/síly). Inerciální soustava je v klidu nebo se pohybuje konstantní rychlostí (protože neexistuje absolutní klid!), zatímco neinerciální soustava je zrychlena (vzhledem k inerciální soustavě).
Pojem referenční soustavy se od dob Aristotela, Galileiho, Newtona a Einsteina výrazně změnil. Více o tom a filozofických implikacích si můžete přečíst v článku Space and Time: Inertial Frames.
Souřadnicová soustava pro analýzu lidského pohybu#
V anatomii používáme zjednodušenou referenční soustavu složenou z kolmých rovin, abychom poskytli standardní referenci pro kvalitativní popis struktur a pohybů lidského těla, jak je znázorněno na dalším obrázku.

Báze souřadnicového systému#
Báze souřadnicového systému je množina vektorů, které nám umožňují jednoznačně popsat polohu libovolného bodu v prostoru. Představte si to jako soustavu os, které se vzájemně protínají v jednom bodě (počátku) a určují směry, ve kterých měříme vzdálenosti.
Proč potřebujeme bázi?
Jednoznačný popis polohy: Díky bázi můžeme každý bod v prostoru jednoznačně identifikovat pomocí souřadnic, které udávají, jak daleko je tento bod od počátku ve směru jednotlivých os.
Zjednodušení výpočtů: Báze nám umožňuje převést geometrické problémy na algebraické, což výrazně usnadňuje jejich řešení.
Standardizace: Báze nám poskytuje společný jazyk pro popis prostorových vztahů.
Jak vypadá báze?
V rovině: Bázi tvoří dva lineárně nezávislé vektory, které určují směr os x a y. Nejčastěji se používá kartézská soustava souřadnic, kde jsou osy x a y kolmé na sebe a mají stejnou jednotku.
V prostoru: Bázi tvoří tři lineárně nezávislé vektory, které určují směr os x, y a z. Opět se nejčastěji používá kartézská soustava souřadnic, kde jsou osy vzájemně kolmé a mají stejnou jednotku.
Vlastnosti báze:
Lineární nezávislost: Žádný vektor báze nesmí být lineární kombinací ostatních vektorů báze.
Rozsah: Počet vektorů v bázi se rovná dimenzi prostoru. V rovině jsou to dva vektory, v prostoru tři.
Ortogonální a ortonormální báze#
Ortogonální báze je speciální typ báze vektorového prostoru, kde jsou všechny vektory vzájemně kolmé. To znamená, že skalární součin libovolných dvou různých vektorů z této báze je roven nule.
Proč je ortogonální báze výhodná?
Jednodušší výpočty: Mnohé výpočty, jako například projekce vektorů nebo hledání souřadnic vektoru vzhledem k bázi, jsou pro ortogonální báze výrazně jednodušší.
Geometrická interpretace: Ortogonálnost vektorů má přímou geometrickou interpretaci - vektory svírají pravý úhel.
Ortonormální báze je ještě speciálnější případ ortogonální báze. Kromě toho, že jsou všechny vektory v této bázi vzájemně kolmé, mají také jednotkovou délku (tj. jejich velikost je rovna jedné).
Proč je ortonormální báze výhodná?
Normalizace: Jednotková délka vektorů zjednodušuje mnohé výpočty, zejména při práci s normami a vzdálenostmi.
Ortogonalita: Zachovává všechny výhody ortogonální báze.
Druhy bází
Kartézská báze: Nejběžnější typ báze, kde osy jsou vzájemně kolmé a mají stejnou jednotku.
Sférická báze: Používá se pro popis polohy bodů ve sférických souřadnicích (poloměr, úhel v horizontální rovině, úhel od vertikály).
Cylindrická báze: Používá se pro popis polohy bodů v cylindrických souřadnicích (poloměr, úhel, výška).
Kartézský souřadnicový systém#
Protože okolní prostor vnímáme jako trojrozměrný, vhodný souřadnicový systém je Kartézsky souřadnicový systém v Kartézkom souřadnicovém systému se třemi ortogonálními osami, jak je znázorněno níže. Ortogonalita kartézského souřadnicového systému je vhodná pro jeho použití v klasické mechanice, většinou se předpokládá, že struktura prostoru má Cartesian coordinate system a v důsledku toho jsou pohyby v různých směrech na sobě nezávislé.

Další iniciativa pro standardizaci referenčních rámců pochází z projektu Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM).
Určení souřadnicového systému#
Nejčastěji používáme kartézskou soustavu souřadnic, která využívá tři vzájemně kolmé osy (x, y, z) a počátek. Každý bod v prostoru můžeme jednoznačně určit pomocí tří čísel, které udávají vzdálenosti od těchto os.
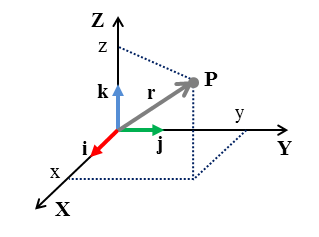
Je vidět, že verzory báze zobrazené na obrázku výše mají v kartézském souřadnicovém systému následující souřadnice:
\begin{equation}
\hat{\mathbf{i}} = \begin{bmatrix}1\0\0 \end{bmatrix}, \quad \hat{\mathbf{j}} = \begin{bmatrix}0\1\0 \end{bmatrix}, \quad \hat{\mathbf{k}} = \begin{bmatrix} 0 \ 0 \ 1 \end{bmatrix}
\end{equation}
Pomocí zápisu popsaného na obrázku výše lze poziční vektor \(\overrightarrow{\mathbf{r}}\) (nebo bod \(\overrightarrow{\mathbf{P}}\)) vyjádřit jako:
\begin{equation}
\overrightarrow{\mathbf{r}} = x \vec{\mathbf{i}} + y \vec{\mathbf{j}} + z\vec{\mathbf{k}}
\end{equation}
Definice báze#
Matematickým problémem určení souřadnicového systému je najít pro něj základ a počátek (základ je pouze množina vektorů bez počátku). Existují různé metody pro výpočet základny dané množinou bodů (souřadnic), například pro tento problém lze použít skalární součin nebo vektorový součin.
Použití vektorového součinu#
Pojďme nyní definovat základ pomocí běžné metody v analýze pohybu (za použití vektorového součinu): Vzhledem k souřadnicím tří nekolineárních bodů ve 3D prostoru (body, které neleží všechny na stejné přímce), \(\overrightarrow{\mathbf{m}}_1, \overrightarrow{\mathbf{m}}_2, \overrightarrow{\mathbf{m}}_3\), které mohou představovat např. polohu značek zachycených z relace analýzy pohybu, lze na základě následujících kroků:
První osa, \(\overrightarrow{\mathbf{v}}_1\), vektor \(\overrightarrow{\mathbf{m}}_2-\overrightarrow{\mathbf{m}}_1\) (nebo jakýkoli jiný vektorový rozdíl);
Druhá osa, \(\overrightarrow{\mathbf{v}}_2\), vektorový součin mezi vektory \(\overrightarrow{\mathbf{v}}_1\) a \(\overrightarrow{\mathbf{m}}_3-\overrightarrow{\mathbf{m}}_1\) (nebo \(\overrightarrow{\mathbf{m}}_3-\overrightarrow{\mathbf{m}}_2\));
Třetí osa, \(\overrightarrow{\mathbf{v}}_3\), vektorový součin mezi vektory \(\overrightarrow{\mathbf{v}}_1\) a \(\overrightarrow{\mathbf{v}}_2\); a
Normalizace vektorů tak, aby měly normu 1, dělení každého vektoru jeho normou.
Polohy bodů použitých ke konstrukci souřadnicového systému musí být podle definice specifikovány ve vztahu k již existujícímu souřadnicovému systému. Při analýze pohybu je tento souřadnicový systém souřadnicovým systémem ze systému zachycení pohybu a je stanoven ve fázi kalibrace. V této fázi jsou pozice značek umístěných na objektu s kolmými osami a známými vzdálenostmi mezi značkami zachyceny a použity jako referenční (laboratorní) souřadnicový systém.
Například vzhledem k pozicím \(\overrightarrow{\mathbf{m}}_1 = [1,2,5], \overrightarrow{\mathbf{m}}_2 = [2,3,3], \overrightarrow{\mathbf{m}}_3 = [4,0,2]\) lze nalézt základ s:
import numpy as np
m1 = np.array([1, 2, 5])
m2 = np.array([2, 3, 3])
m3 = np.array([4, 0, 2])
v1 = m2 - m1 # první osa
v2 = np.cross(v1, m3 - m1) # druhá osa
v3 = np.cross(v1, v2) # třetí osa
# Vektorová normalizace
e1 = v1/np.linalg.norm(v1)
e2 = v2/np.linalg.norm(v2)
e3 = v3/np.linalg.norm(v3)
print('Verzory:', '\ne1 =', e1, '\ne2 =', e2, '\ne3 =', e3)
print('\nNorm of každého z verzorů:',
'\n||e1|| =', np.linalg.norm(e1),
'\n||e2|| =', np.linalg.norm(e2),
'\n||e3|| =', np.linalg.norm(e3))
print('\nTest of ortogonality (pomocí vektorového součinu):',
'\ne1 x e2:', np.linalg.norm(np.cross(e1, e2)),
'\ne1 x e3:', np.linalg.norm(np.cross(e1, e3)),
'\ne2 x e3:', np.linalg.norm(np.cross(e2, e3)))
Verzory:
e1 = [ 0.40824829 0.40824829 -0.81649658]
e2 = [-0.76834982 -0.32929278 -0.5488213 ]
e3 = [-0.49292179 0.85141036 0.17924429]
Norm of každého z verzorů:
||e1|| = 1.0
||e2|| = 1.0
||e3|| = 1.0
Test of ortogonality (pomocí vektorového součinu):
e1 x e2: 1.0
e1 x e3: 1.0000000000000002
e2 x e3: 0.9999999999999999
Kvůli chybám zaokrouhlování (blíže tady) a nepřesnosti výpočtu s desetinnými čísly s plovoucí desetinnou čárkou (blíže tady) se normy přesně nerovnají 1. V případě potřeby můžeme výsledek zaokrouhlit:
print('\nTest of orthogonality (pomocí vektorového součinu):',
'\ne1 x e2:', np.linalg.norm(np.cross(e1, e2)).round(8),
'\ne1 x e3:', np.linalg.norm(np.cross(e1, e3)).round(8),
'\ne2 x e3:', np.linalg.norm(np.cross(e2, e3)).round(8))
Test of orthogonality (pomocí vektorového součinu):
e1 x e2: 1.0
e1 x e3: 1.0
e2 x e3: 1.0
Nebo formátujte text představující výsledek:
print('\nTest of orthogonality (pomocí vektorového součinu):',
f'\ne1 x e2: {np.linalg.norm(np.cross(e1, e2)):g}',
f'\ne1 x e3: {np.linalg.norm(np.cross(e1, e3)):g}',
f'\ne2 x e3: {np.linalg.norm(np.cross(e2, e3)):g}')
Test of orthogonality (pomocí vektorového součinu):
e1 x e2: 1
e1 x e3: 1
e2 x e3: 1
Kde jsme použili f'{:.g}' k formátování čísla na řetězec (blíže tady nebo tady).
Pro trvalou změnu bychom mohli použít numpy nastavení pro reprezentaci přesnosti desetinné čárky s funkcí np.set_printoptions, ale ta funguje pouze pro numpy pole, ne s čísly. Nebo použijte kouzelný příkaz IPython np.set_printoptions, ale v tomto případě nemůžete použít funkci print pro zobrazení výsledku.
Definice počátku#
Abychom mohli definovat souřadnicový systém pomocí vypočítané báze, musíme také definovat počátek. V zásadě bychom mohli jako počátek použít jakýkoli bod, ale pokud by se měl vypočítaný souřadnicový systém řídit anatomickými konvencemi, např. počátek souřadnicového systému by měl být ve středu kloubu, budeme muset vypočítat bázi a počátek podle standardů používaných v analýze pohybu.
Pokud je souřadnicový systém technickým základem a nikoli anatomickým, běžným postupem při analýze pohybu je definovat počátek souřadnicového systému jako těžiště (průměrnou) polohu mezi značkami v referenčním rámci. Použití průměrné polohy napříč značkami potenciálně snižuje vliv šumu (například z artefaktu měkkých tkání) na výpočet.
Pro značky ve výše uvedeném příkladu bude počátek souřadného systému:
origin = np.mean((m1, m2, m3), axis=0)
print('Počátek: ', origin)
Počátek: [2.33333333 1.66666667 3.33333333]
Nakreslete souřadnicový systém a základ pomocí vlastní funkce Pythonu CCS.py.
Můžeme sem zkopírovat a vložit obsah souboru CCS.py (a spustit buňku) nebo můžeme funkci načíst z adresáře, udělejme to. Nejprve vytvořte složku “functions” a umístěte do ní soubor CCS.py.
path2 = r'./functions'
import sys
sys.path.insert(1, path2) # přidat do pythonpath
from CCS import CCS
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
/tmp/ipykernel_342344/3498384649.py in <module>
2 import sys
3 sys.path.insert(1, path2) # přidat do pythonpath
----> 4 from CCS import CCS
ModuleNotFoundError: No module named 'CCS'
markers = np.vstack((m1, m2, m3))
basis = np.vstack((e1, e2, e3))
Vizualizace souřadnicového systému#
Abychom měli interaktivní graf matplotlib, musíme před prvním použitím nainstalovat knihovnu ipympl a restartovat prostředí Google Colab.
!pip3 install -q ipympl
%matplotlib widget
CCS(xyz=[], Oijk=origin, ijk=basis, point=markers, vector=True);
Gramův–Schmidtův proces#
Další klasický postup v matematice, využívající skalární součin, je známý jako Gram–Schmidt process. Podívejte se na wikipedii Gram–Schmidt process, kde je ukázka Gram–Schmidtova procesu a jak jej implementovat v Pythonu.
Gram–Schmidt process je metoda pro ortonormalizaci (ortogonální jednotkové versory) sady vektorů pomocí skalárního součinu. Gram-Schmidtův proces funguje pro libovolný počet vektorů.
Například za předpokladu tří vektorů \(\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}\), ve 3D prostoru lze základ \(\{\vec{e}_a, \vec{e}_b, \vec{e}_c\}\) nalézt pomocí procesu Gram–Schmidta
První versor je v
\(\overrightarrow{\mathbf{a}}\) směr (nebo ve směru kteréhokoli z dalších vektorů):
\begin{equation}
\vec{e}_a = \frac{\overrightarrow{\mathbf{a}}}{||\overrightarrow{\mathbf{a}}||}
\end{equation}
Druhý versor, ortogonální k \(\vec{e}_a\), lze nalézt za předpokladu, že můžeme vyjádřit vektor \(\overrightarrow{\mathbf{b}}\) ve směru \(\vec{e}_a\) jako:
\begin{equation}
\overrightarrow{\mathbf{b}} = \overrightarrow{\mathbf{b}}^| + \overrightarrow{\mathbf{b}}^\bot
\end{equation}
Pak:
\begin{equation} \overrightarrow{\mathbf{b}}^\bot = \overrightarrow{\mathbf{b}} - \overrightarrow{\mathbf{b}}^\| = \overrightarrow{\mathbf{b}} - (\overrightarrow{\mathbf{b}} \cdot \vec{e}_a ) \vec{e}_a \end{equation}Konečně:
\begin{equation} \vec{e}_b = \frac{\overrightarrow{\mathbf{b}}^\bot}{||\overrightarrow{\mathbf{b}}^\bot||} \end{equation}Třetí versor, ortogonální k \(\{\vec{e}_a, \vec{e}_b\}\), lze nalézt vyjadřující vektor \(\overrightarrow{\mathbf{C}}\) ve směrech \(\vec{e}_a\) a \(\vec{e}_b\) jako:
\begin{equation}
\overrightarrow{\mathbf{c}} = \overrightarrow{\mathbf{c}}^| + \overrightarrow{\mathbf{c}}^\bot
\end{equation}
Pak: \begin{equation} \overrightarrow{\mathbf{c}}^\bot = \overrightarrow{\mathbf{c}} - \overrightarrow{\mathbf{c}}^| \end{equation}
Kde: \begin{equation} \overrightarrow{\mathbf{c}}^| = (\overrightarrow{\mathbf{c}} \cdot \vec{e}_a ) \hat{e}_a + (\overrightarrow{\mathbf{c}} \cdot \vec{e}_b ) \hat{e}_b \end{equation}
Konečně: \begin{equation} \vec{e}_c = \frac{\overrightarrow{\mathbf{c}}^\bot}{||\overrightarrow{\mathbf{c}}^\bot||} \end{equation}
A animace probíhajícího Gram-Schmidtova procesu:

Pojďme implementovat Gram–Schmidtův proces v Pythonu.
Například vzhledem k pozicím, které jsme viděli dříve, \(\overrightarrow{\mathbf{m}}_1 = [1,2,5], \overrightarrow{\mathbf{m}}_2 = [2,3,3], \overrightarrow{\mathbf{m}}_3 = [4,0,2]\), základ lze nalézt s:
První verze je:
ea = m1/np.linalg.norm(m1)
print(ea)
[0.18257419 0.36514837 0.91287093]
Druhý versor je:
eb = m2 - np.dot(m2, ea)*ea
eb = eb/np.linalg.norm(eb)
print(eb)
[ 0.59020849 0.70186955 -0.39878952]
A třetí verzor je:
ec = m3 - np.dot(m3, ea)*ea - np.dot(m3, eb)*eb
ec = ec/np.linalg.norm(ec)
print(ec)
[ 0.78633365 -0.61159284 0.08737041]
Pojďme zkontrolovat ortonormalitu mezi těmito versory:
print(" Versors:", "\nea =", ea, "\neb =", eb, "\nec =", ec)
print(
"\n Norma každého verzoru:",
"\n ||ea|| =",
np.linalg.norm(ea),
"\n ||eb|| =",
np.linalg.norm(eb),
"\n ||ec|| =",
np.linalg.norm(ec),
)
print(
"\n Test ortogonality (skalární součin):",
"\n ea . eb:",
np.dot(ea, eb),
"\n eb . ec:",
np.dot(eb, ec),
"\n ec . ea:",
np.dot(ec, ea),
)
Versors:
ea = [0.18257419 0.36514837 0.91287093]
eb = [ 0.59020849 0.70186955 -0.39878952]
ec = [ 0.78633365 -0.61159284 0.08737041]
Norma každého verzoru:
||ea|| = 1.0
||eb|| = 1.0
||ec|| = 1.0
Test ortogonality (skalární součin):
ea . eb: -3.3306690738754696e-16
eb . ec: 6.245004513516506e-17
ec . ea: 8.326672684688674e-17
Vizualizace souřadnicového systému#
# zkus to sám
Sférický souřadnicový systém#
Souřadnice sférické jsou trojrozměrný souřadnicový systém, který využívá k určení polohy bodu v prostoru:
Radiální vzdálenost (\(\rho\)): Vzdálenost bodu od počátku souřadnic.
Azimutální úhel (\(\theta\)): Úhel v rovině xy mezi kladnou osou x a projekcí bodu do této roviny.
Zenitový úhel (\(\phi\)): Úhel mezi kladnou osou z a spojnicí bodu s počátkem.

Báze sférických souřadnic
Bázi sférických souřadnic tvoří tři jednotkové vektory:
\(\vec{\mathbf{e}}_\rho\): Směřuje radiálně od počátku k bodu.
\(\vec{\mathbf{e}}_\theta\): Směřuje ve směru rostoucího azimutálního úhlu \(\theta\).
\(\vec{\mathbf{e}}_\varphi\): Směřuje ve směru rostoucího zenitového úhlu \(\varphi\).
Tato báze je ortonormální, což znamená, že vektory jsou vzájemně kolmé a mají jednotkovou velikost.
Transformace z kartézských souřadnic
Pro převod kartézských souřadnic (\(x, y, z\)) na sférické souřadnice (\(\rho, \theta, \varphi\)) platí následující vztahy:
\(\rho = \sqrt{x^2 + y^2 + z^2}\)
\(\theta = \arctan{\frac{y}{x}}\)
\(\varphi = \arccos{\frac{z}{\rho}}\)
Transformace do kartézských souřadnic
Pro převod sférických souřadnic na kartézské souřadnice platí následující vztahy:
\(x = \rho \sin{\varphi} \cos{\theta}\)
\(y = \rho \sin{\varphi} \sin{\theta}\)
\(z = \rho \cos{\varphi}\)
Výhody sférických souřadnic:
Symetrie: Využívají se výhodně pro problémy s kulovou symetrií (např. gravitační pole, elektrostatické pole).
Zjednodušení výpočtů: V některých případech mohou zjednodušit řešení fyzikálních problémů.
Nevýhody sférických souřadnic:
Složitější derivace: Výpočet gradientu, divergence a rotace v sférických souřadnicích je složitější než v kartézských.
Singularity: V počátku souřadnic (ρ = 0) a na pólech (φ = 0, π) mohou nastat singularity.
IFrame('https://www.geogebra.org/classic/c5nsjx3t?embed')
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/tmp/ipykernel_28856/37843828.py in <module>
----> 1 IFrame('https://www.geogebra.org/classic/c5nsjx3t?embed')
NameError: name 'IFrame' is not defined
Cylindrické souřadnice#
Cylindrické souřadnice jsou vhodné pro systémy s válcovou symetrií. Používají se tři souřadnice:
Radiální vzdálenost (ρ): Vzdálenost bodu od osy z.
Azimutální úhel (θ): Úhel v rovině xy měřený od kladné osy x.
Výška (z): Vzdálenost bodu od roviny xy (stejná jako v kartézských souřadnicích).
Transformační vztahy:
Z cylindrických do kartézských:
\(x = \rho \cos{\theta}\)
\(y = \rho \sin{\theta}\)
\(z = z\)
Z kartézských do cylindrických:
\(\rho = \sqrt{x^2 + y^2}\)
\(\theta = \arctan{\frac{y}{x}}\)
\(z = z\)
IFrame('https://www.geogebra.org/classic/X3j28ZkC?embed', width='100%', height=500)
Srovnání:
Vlastnost |
Kartézské |
Sférické |
Cylindrické |
|---|---|---|---|
Symetrie |
Obdélníková |
Kulová |
Válcová |
Souřadnice |
x, y, z |
ρ, θ, φ |
ρ, θ, z |
Použití |
Obecné |
Kulová symetrie |
Válcová symetrie |
Kdy použít který systém?
Kartézské: Většina každodenních problémů, lineární pohyb.
Sférické: Problémy s kulovou symetrií (např. gravitace, elektrostatika).
Cylindrické: Problémy s válcovou symetrií (např. proudění tekutin v potrubí).
Proč používat jiné souřadnicové systémy než kartézské?
Zjednodušení výpočtů: Problémy s určitou symetrií mohou být v jiných souřadnicových systémech jednodušší.
Přirozenější popis: Některé fyzikální jevy jsou přirozeněji popsány v jiných souřadnicových systémech.
Další čtení#
Video přednášky na internetu#
Problémy#
Jak rychle se právě teď pohybujete? Ve své odpovědi zvažte svůj pohyb ve vztahu k Zemi a ve vztahu ke Slunci.
Přejděte na webovou stránku http://www.wisc-online.com/Objects/ViewObject.aspx?ID=AP15305 a dokončete interaktivní lekci, kde se dozvíte o anatomické terminologii pro popis relativní polohy v lidském těle.
Chcete-li se dozvědět více o kartézských souřadnicových systémech, přejděte na webovou stránku http://www.mathsisfun.com/data/cartesian-coordinates.html, prostudujte si materiál a odpovězte na 10 otázek na konci.
Zadané body v 3D prostoru, m1 = [2, 2, 0], m2 = [0, 1, 1], m3 = [1, 2, 0], najděte ortonormální bázi.
Určete, zda následující body tvoří základ v 3D prostoru, m1 = [2, 2, 0], m2 = [1, 1, 1], m3 = [1, 1, 0].
Odvoďte výrazy pro tři osy páneve s ohledem na konvenci projektu Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM) (každý použijte RASIS, LASIS, RPSIS a LPSIS jako názvy pro axi orientační bod pánve a výraz).
Určete vektorovou bázi pro pánev podle konvence projektu Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM) pro následující polohy anatomických orientačních bodů (jednotky v metrech): RASIS=[0.5, 4] 0.8, 70 . 0,1], RPSIS = [0,3, 0,85, 0,2], LPSIS = [0,29, 0,78, 0,3].
Reference#
Corke P (2017) Robotics, Vision and Control: Fundamental Algorithms in MATLAB. 2. vyd. Springer-Verlag Berlín.
Stanfordská encyklopedie filozofie. Space and Time: Inertial Frames.
