Vzpěr

Ztráta stability vzpěrem je náhlá deformace konstrukčního prvku zatíženého tlakem, která nastává, když tlakové zatížení prvku dosáhne kritické hodnoty.

Vzpěr se často projevuje náhle a může vést k velkým posunům. I když nemusí vždy dojít k porušení materiálu (vzniku trhlin nebo porušení), vzpěr se považuje za selhání, protože vzpěrá konstrukce již nemůže plnit svou původní funkci.

Eulerův vztah pro vzpěr

Problém stability osově zatíženého prutu vyřešil již r. 1744 Leonard Euler (1707 – 1783). Technici jeho poznatky zpočátku nebrali na vědomí – až do doby, kdy došlo k zřícení několika příhradových železničních mostů v počátečním stadiu rozvoje železnice. (Největší havárie se stala v polovině 19. století ve Švýcarsku – rodné zemi Eulera.) Od té doby platí přísné normy pro kontrolu vzpěrné pevnosti osově stlačovaných prutů.

Eulerův vztah se používá k výpočtu axiálního zatížení \(F_\mathrm{krit}\), při kterém prut nebo nosník ztrácí stabilitu. Tuto sílu nazýváme kritickou silou na mezi vzpěrné pevnosti. Při kritickém zatížení jakákoli malá odchylka, ať už se jedná o boční sílu nebo malou nedokonalost v geometrii prutu, způsobí ztrátu stability.

\[F_\mathrm{krit} = \frac{\pi^2 EJ_{\mathrm{min}}}{l_\mathrm{red}^2}\]

Kritické zatížení závisí pouze na třech parametrech:

• Youngově modulu \(E\) materiálu

• kvadratickém momentu průřezu \(J_\mathrm{min}\) – v případě různých hlavních kvadratických momentů se bere ten menší

• redukovaná délka \(l_\mathrm{red}\) prutu.

Redukovaná délka a okrajové podmínky

Způsob, jakým jsou konce prutu nebo nosníku omezeny, ovlivní kritické vzpěrné zatížení. Prut, který je na jednom konci pevně uchycen a na druhém volný, bude zjevně schopen unést mnohem menší zatížení před vzpěrem ve srovnání s tím, který je na obou koncích kloubově uložen. Tvary vzpěru jsou také zcela odlišné.

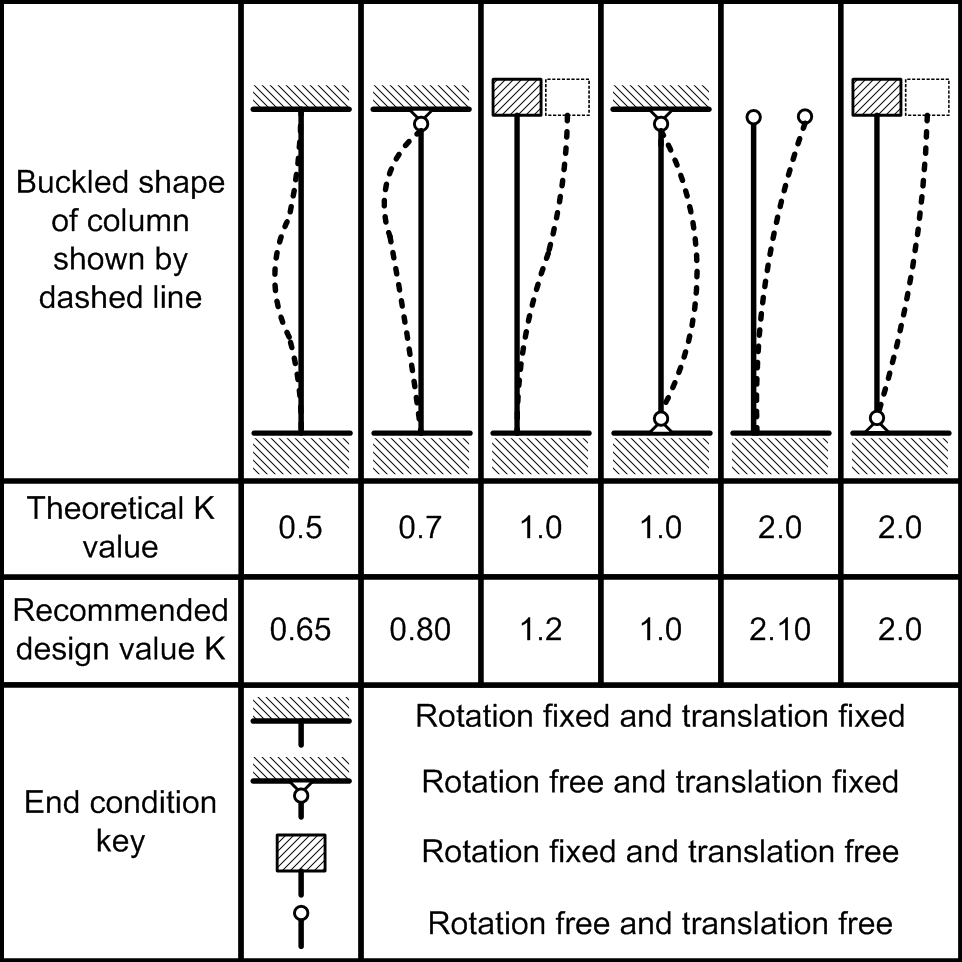
Eulerův vzorec zohledňuje různé koncové podmínky pomocí parametru redukované délky \(l_\mathrm{red}\).

Prut, který je kloubově uložen na obou koncích, má efektivní délku, která se rovná délce sloupu. Ostatní koncové podmínky vedou k efektivní délce, která se rovná délce vynásobené specifickým faktorem. Tyto faktory jsou uvedeny v tabulce níže pro několik různých koncových podmínek.

Koncové podmínky	Efektivní délka
Kloubové uložení na obou koncích	\(l = l_\mathrm{red}\)
Vetknutí na jednom konci, volný konec na druhém	\(l_\mathrm{red} = 2 l\)
Vetknutí na obou koncích	\(l_\mathrm{red} = 0.5 l\)
Vetknutí na jednom konci, kloubové na druhém	\(l_\mathrm{red} = 0.7 l\)

Souhrnné listy Efficient Engineer

Štíhlost prutu

I bez znalosti Eulerova vzorce je intuitivně zřejmé, že štíhlé sloupy jsou mnohem více ohroženy vzpěrem než silné. Proto jsou prvky příhradové konstrukce, které jsou zatíženy tlakem, někdy navrženy tak, aby byly silnější než ty, které jsou zatíženy tahem, a proto se používají výztužné prvky, které zabraňují vzpěru dlouhých tlakových prvků.

Eulerův vzorec potvrzuje tuto intuici – délkový člen v rovnici je na druhou, a v důsledku toho zdvojnásobení délky sloupu znamená, že může unést pouze čtvrtinu zatížení před vzpěrem.

Pro lepší pochopení vlivu štíhlosti je užitečné zavést bezrozměrný parametr nazvaný štíhlost \(\lambda\), který definuje, jak štíhlý je sloupec (tj. jak tenký je ve srovnání s jeho délkou).

\[\lambda = \frac{l_{red}}{\sqrt{\frac{J_{min}}{A}}} \]

Reálný prut má konečnou hodnotu meze kluzu. Nabízí se tedy otázka, zda pro daný prut nastane dříve mezní stav pružnosti nebo vzpěrné stability. Když vydělíme kritickou sílu podle Eulera plochou průřezu prutu získáme:

\[\sigma_\mathrm{krit} = \frac{F_\mathrm{krit}}{A} = \pi^2 \frac{E J_{min}}{A l_\mathrm{red}^2} = \pi^2 \frac{E}{\lambda^2}\]

Jak již bylo zmíněno, je intuitivní, že štíhlost sloupu významně ovlivní, jaké zatížení unese před vzpěrem, proto je zajímavé podívat se na to, jak se Eulerovo kritické vzpěrné napětí mění s štíhlostním poměrem – to je znázorněno na grafu níže.

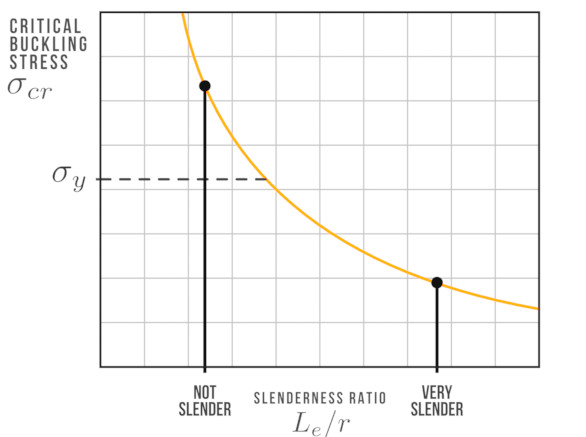
Velmi štíhlé sloupy mají velký štíhlostní poměr a velmi nízké kritické vzpěrné napětí. U silných sloupů s nízkým štíhlostním poměrem bude kritické vzpěrné napětí velmi vysoké.

Přerušovaná vodorovná čára na grafu výše ukazuje mez kluzu materiálu sloupu v tlaku \(\sigma_K\). U velmi nízkých štíhlostních poměrů bude mez pevnosti materiálu překročena dříve, než bude dosaženo meze vzpěru. To znamená, že můžeme definovat dvě odlišné oblasti, jednu, kde sloupy selhávají drcením, protože napětí ve sloupu překračuje mez kluzu materiálu (tj. u silných sloupů), a jednu, kde selhávají v důsledku vzpěru (tj. u štíhlých sloupů).

Tato křivka představuje pouze teoretické chování sloupů. Pokud vykreslíme vzpěrná napětí určená experimentálně pro skutečné sloupy, uvidíme, že se přesně neshoduje s teoretickým chováním – to je znázorněno na grafu níže. Zejména přechod mezi plastickým selháním (drcení) a elastickým selháním (vzpěr) je mnohem plynulejší. Je to proto, že u sloupů v tomto přechodném rozsahu je vzpěr ve skutečnosti složitou kombinací těchto dvou způsobů selhání. Vzpěr v této přechodné oblasti se nazývá nepružný vzpěr a měl by být modelován pomocí metod, jako je Engesserova teorie nebo Shanleyho teorie, spíše než Eulerův vzorec.

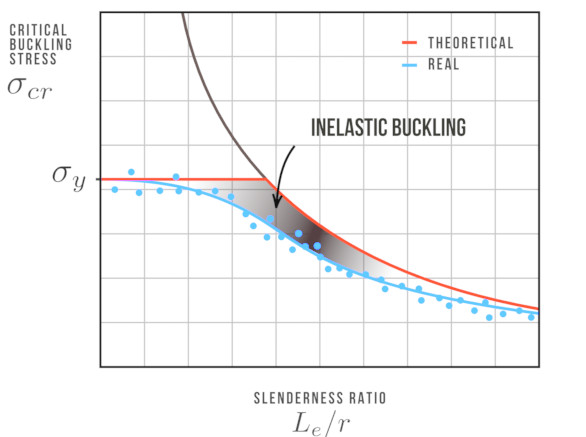
Mnoho průmyslových návrhových norem zahrnuje křivky podobné těm, které jsou uvedeny výše, které lze použít pro návrh prvků zatížených tlakem.