3. cvičení#
Kinematika oscilátoru#
Ultrazvukové přístroje používají lékaři k pořizování snímků pro vyšetření vnitřních orgánů těla. Ultrazvukový přístroj vysílá vysokofrekvenční zvukové vlny, které se odrážejí od orgánů, a počítač přijímá vlny a používá je k vytvoření obrazu. Uvažujme lékařské zobrazovací zařízení, které produkuje ultrazvuk oscilací s periodou \(0,400\,\mu \text{s}\). Jaká je frekvence tohoto kmitání? Je možné ho slyšet?
Blok o hmotnosti 2,00 kg je umístěn na povrchu bez tření. Pružina s tuhostí \(k=32,00\,\text{N}\text{/}\text{m}\) je připevněna k bloku a opačný konec pružiny je připevněn ke stěně. Pružina může být stlačena nebo prodloužena. Rovnovážná pozice je označena jako \( x=0,00\,\text{m}\).
Na blok působí externí síla praxí a umístní ho do polohy \(x=+0,02\,\text{m}\). Blok se uvolní z klidu a osciluje mezi \(x=+0,02\,\text{m}\) a \(x=-0,02\,\text{m}\). Perioda pohybu je 1,5 s. Určete úhlovou rychlost a zapište rovnice. Numericky a graficky zdůvodněte průbeh rychlosti \(a\) a zrychlení \(v\).
Dokažte, že pro popis kmitání \(x(t)=A\text{sin}(\omega t+\varphi )\) není perioda funkcí počátečné fáze. Proč si k popisu vybíráme funkci \(\cos\) a ne \(\sin\)?
Pneumatika má vzorek běhounu se štěrbinou každých 2,00 cm. Každá štěrbina vytváří při pohybu pneumatiky sílu. Jaká je frekvence těchto sil, pokud se auto pohybuje rychlostí 30,0 m/s? Jedná se o harmonické buzení?
Volné kmity#
Níže uvedený graf ukazuje údaje o poloze malého masivního vozíku připojeného k pružině, jak je znázorněno na obrázku.
určete periodu \(T\)
určete frekvenci \(f\)
určete úhlovou rychlost \(\omega\)
pokud je tuhost pružiny \(k\)=2,5 N/m, můžete zjistit hmotnost vozíku? Pokud můžete, udělejte to a vysvětlete své úvahy. Pokud nemůžete, vysvětlete, proč ne.


Hmota \({m}_{0}\) je připevněna k pružině a visí svisle. Hmota se zvedne o krátkou vzdálenost ve vertikálním směru a uvolní se. Hmota kmitá s frekvencí \({f}_{0}\). Pokud je hmota nahrazena hmotou devětkrát větší a experiment se opakuje, jaká by byla frekvence oscilací ve smyslu \({f}_{0}\)?
Hmota o hmotnosti 0,500 kg zavěšená na pružině kmitá s periodou 1,50 s. Kolik hmoty je třeba přidat k objektu, aby se perioda změnila na 2,00 s?
Jakou chybu (procentuální i hmotnostní) byste měli při výběru hmotnosti objektu v předchozí úloze, pokud byste si přáli, aby nová perioda byla větší než 2,01 s nebo menší než 1,99 s?
Jednoduchá hmota na pružině je základem pro náš popis téměř jakéhokoli kmitání. Podívejme se na vibrační stavy jednoduché dvouatomové molekuly, řekněme N\(_2\). Pokud se podíváme pouze na oscilace molekuly, kde se těžiště nepohybuje, atomy se pohybují stejně a opačně. Když jeden jde doleva, druhý jde stejnou rychlostí doprava a naopak. Je to jako dva vozíky připevněné ke zdi a kmitající rovnoměrně a opačně, jak je znázorněno na spodním obrázku. Když se každý vozík posune o vzdálenost \(x\), pružina mezi atomy se ve skutečnosti natáhne na vzdálenost \(2x\), takže síla na každý atom je \(−2kx\). V případě symetrické molekuly tak můžeme tedy použít jeden model „vozík na pružině“ pro každý z atomů, pokud nahradíme \(k\) hodnotou \(2k\).
Je-li úhlová frekvence kmitání N\(_2\) je 4,5 10\(^{-18}\) rad/s, a hmotnost jednoho atomu dusíku je 2,3 x 10\(^{-26}\) kg, najděte efektivní tuhost vazby mezi dvěma atomy.
Některé z excitací dvouatomové molekuly, jako je \(HCl\), lze modelovat jako dvě hmoty spojené pružinou. Ačkoli klasický model není zcela správný (viz. Kvantové oscilátory a jejich diskrétní stavy), můžeme použít odhadnout frekvenci, abychom získali určitý pocit síly efektivní pružiny, která spojuje molekuly. Doba přechodu z rovnovážné polohy do maximálního roztažení trvá asi \(3 10^{–15}\) s. Hmotnost atomu \(H\) je přibližne 1 \(u\) a hmotnost atomu \(Cl\) je 35 \(u\) kde \(u\) je atomová hmotnostní konstanta 1,66 10\(^{−27}\) kg.
Odhadněte efektivní tuhost chemické vazby

Blok o hmotnosti \(M\) je v klidu na vodorovném stole bez tření. K pevné podpěře je připevněn pružinou o konstantní tuhosti \(k\). Hliněná peleta o hmotnosti \(m\) a rychlosti \(v\) narazí na blok, jak je znázorněno na obrázku, a přilepí se k němu.
Určete rychlost kvádru bezprostředně po srážce.
Určete amplitudu výsledného jednoduchého harmonického pohybu.
Odvoďte rovnici kmitání.
Abyste mohli tento problém vyřešit, musíte provést řadu zjednodušujících předpokladů, z nichž některé jsou v problému uvedeny a některé nikoli. Diskutujte o aproximacích, které jste museli udělat, abyste problém vyřešili.

Hmota visící na pružině natáhne pružinu, visící v klidu v rovnovážné poloze, kde je síla pružiny směrem nahoru vyvážena gravitační silou směřující dolů. Pokud se hmota stáhne a uvolní, bude oscilovat. Na obrázku je zobrazeno 5 fotografií okamžiku, kdy visící hmota osciluje. Červená šipka ukazuje gravitační sílu na hmotu v tomto okamžiku a modrá šipka ukazuje sílu, kterou v tomto okamžiku působí pružina. Zvolíme nulovou hladinu gravitační potenciální energie na červené čáře ve spodní části obrázku, jak je znázorněno.
Pokud se pružina trochu natáhne a uvolní, osciluje z C do B do D zpět do B atd.
Pokud se pružina hodně natáhne a uvolní, osciluje z E do B do F zpět do B atd.
Jak byste seřadili potenciální energii pružiny pro malé kmitání (obrázky B, C a D)?
Jak byste seřadili potenciální energie pružiny pro velkou oscilaci B, E a F?
Jak byste seřadili kinetické energie hmot od nejvyšší po nejnižší pro pět zobrazených okamžiků?
Jak byste seřadili gravitační potenciální energie od nejvyšší po nejnižší pro uvedených pět okamžiků?

Uvažujme hmotu \(m\) s pružinami podle obrázku. Nechť jsou tuhosti pružin \(k_1\) a \(k_2\). Řešte pohybovou rovnici a určte fekvenci vlastních kmitů.

Určete vlastní frekvenci systému.

Tlumené kmity#
UVažujte, pohybovou rovnici danou
\[\ddot{x} + 2 \ddot{x} + (\omega^2 +1) x = 2 \cos \omega t\]Určete všechny působící síly a vysvětlete jejich původ.
Plastová láhev je částečně naplněna pískem a umístěna do vody. Kombinovaná hmotnost láhve a písku je \(m\). V rovnováze je dno láhve ve vzdálenosti \(d\) z hladiny vody. Hustota vody je a gravitační zrychlení je \(g\). Plocha dna lahve je \(A\). Jemným šťouchnutím se láhev bude jemně kývat nahoru a dolů s periodou \(T\).
v případě, že zanedbáme tření určete všechny síly a řešte pohybovou rovnici. Dokažte, že se jedná o periodický pohyb a určete jeho frekvenci.
uvažujte vizkózní tření (odporová síla úměrná rychlosti pohybu), od čeho závisí pohyb láhve?
předpokládejte, že amplituda kmitu láhve klesá s časovou konstantou \(\tau\). Zapište závislost \(x(t)\).
změníme-li hmotnost písku, jak se změní frekvence kmitů.

Kyvadlo#
Kulka o hmotnosti \(m\) je vypálena do stacionárního bloku hmoty \(M\) o určité rychlosti \(v\). Blok se vychýli o hodnotu \(h\). Délka závěsu je \(l\).
Vysvětlete, proč nelze použít zachování energie před srážkou?
Předpokládejme, že blok je 100krát těžší než střela. Pokud se systém kulka-blok vykývne do výšky 20 cm, jaká byla počáteční rychlost kulky? Předpokládejme, že experiment probíhá je na Zemi.
Popište závislost vychýlení na čase \(\varphi(t)\).

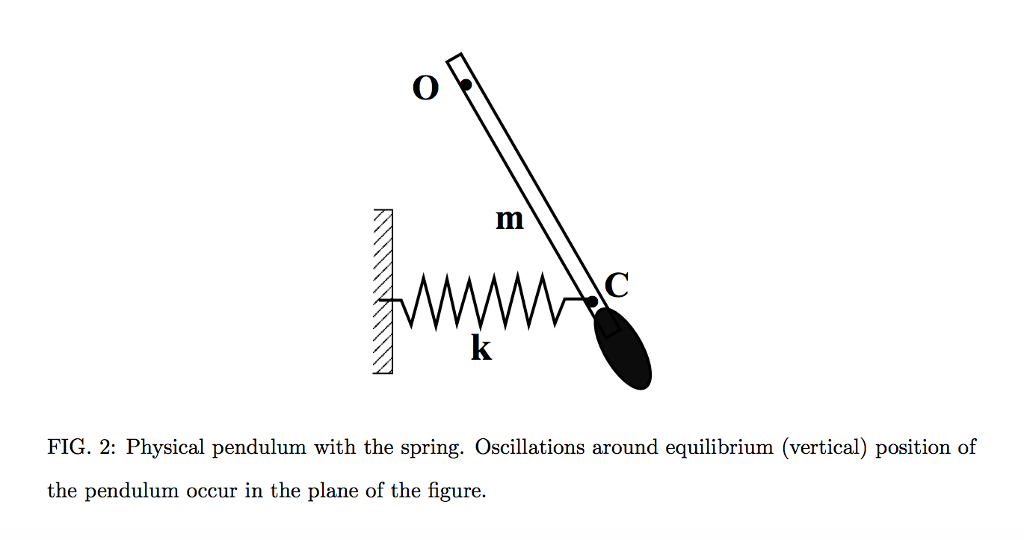
Určete rovnice pohybu pro soustavu kyvadla a pružiny.
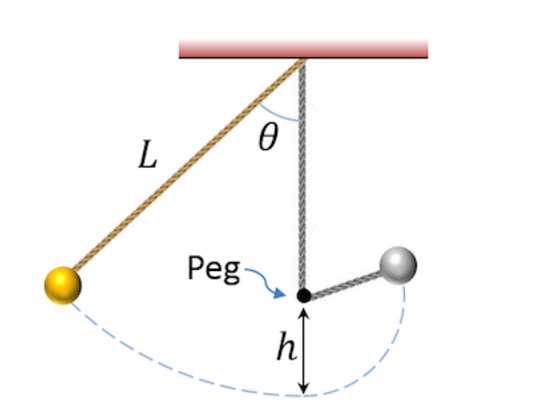
Z malé koule o hmotnosti \(m\) = 1,00 kg na lehké, ale pevné struně o délce \(L\) = 1,50 m je vytvořeno kyvadlo. Kolíček je upevněn tak, aby seděl ve vzdálenosti \(h = L/2\) nad nejnižším bodem výkyvu kyvadla, jak je znázorněno níže. Velikost kolíčku je oproti délce provázku zanedbatelná. Z jakého minimálního úhlu? musí být kyvadlo uvolněno, aby kulička dosáhla polohy přímo nad kolíkem, aniž by se provázek prověsil? (Tip: struna se prověsí, pokud napětí v ní klesne na nulu.)