Škálování

Nervy v páteřní míše mají délku až jednoho metru. Proč ale neexistuje buňka, která by měla nejen délku jednoho metru ale také šírku a výšku jednoho metru. Proč na úrovní centrimetrů je nejúspěšnejším žívočišným druhem hmyz, zatímco obratlovci dominují v rozměrech decimentrů až metrů. Odpověď na tuto otázku je až překvapivě jednoduchá a pro úvahu nám stačí znát poměr mezi objemem a plochou.

Rozměry živých organizmů

Délka organizmu je, jak jsem si řekli v předešlé kapitole, jedna ze základních charakteristik organizmů. Živé organizmy existují v široké škále velikostí, který si můžeme lépe uvědomit, porovnáme-li velikost bakterie a velryby. Velryba má rozměr v desítkách metrů (10\(^1s\)), zatímco bakterie jsou mikroskopičtí živočichové o rozměrech desetin mikrometrů (\(10^{-7}\) m). Rozdíl v délce je tedy 8 řádů. Má-li jedna bakterie objem približně (0.1\(\mu\)m)\(^3\) a velryba objem (10 m)\(^3\), vejde se do jedné velryby celkově 10\(^{24}\) bakterií.

Protože my jsme spíš zvyklí posuzovat rozměry na základě délky než objemu a uvažujeme v relativně malých číslech, informace, že do objemu velryby se vejde 10\(^{24}\) bakterií je pro nás nepředstavitelné číslo. Jaká je to délka kdybychom tyto bakterie seřadili za sebou? Můžete si jednoduše spočítat, že takový řetezec bakterií by obtočil Zemi kolem rovníku 7.6 miliard krát, nebo bychom je mohli nátáhnout až ke Slunci a zpátky k Zemi až milionkrát. Případně bychom mohli tyto bakterie roztáhnout k nejbližší hvězdě, což je 3.3 světelného roku a zpátky celkově 5 krát. Samozřejmě, že tato úvaha není právě jednoduchá, poskytuje nám ovšem představu o složitosti živých organizmů.

Délka, plocha, objem

Představte si živý organizmus, který by měl tvar krychle, označme ho krychloid. Organizmus by byl tvořen z větší části z vody, měl by tedy hustotu 1000 kg m\(^{-3}\). Krychle by měla stranu \(l_1=\)1 dm. Jaký by měla povrch a jaký by měla objem a hmotnost? Z geometrie víme, že krychle má 6 stran a každá strana je čtverec, povrch je tedy

\[A_1=6l_1^2 = 6\,\mathrm{dm}^2.\]

Objem krychle je úměrný třetí mocnině strany

\[V_1 = l_1^3 = 1\,\mathrm{dm}^3.\]

Jeden decimetr krychlový se rovná 0.001 m\(^3\) pro odvození hmotnosti můžeme vyjít z jednotek hustoty, které jsou definovány jako poměr hmotnosti na objem. Hustota se tedy počítá jako \(\rho = m/V\) a pro našeho krychloida bude mít hodnotu 1 kg.

Krychloid je ve svém okolí spokojen a roste. Jeho hustota zůstává stejná, ale naroste do dvojnásobného rozměru, označme ho dolním indexem 2. Znamená to, že jeho lineární rozměr, tedy délka je

\[l_2 = 2\,l_1,\]

tedy hrana krychloida měří 2 dm. Jak se změní jeho plocha, objem a hmotnost? Jeho plocha se určí stejným způsobem jako v předešlém případě. Plocha krychle je

\[V_2 = 6 (l_2)^2\]

tedy 24 dm\(^3\). V porovnání s plochou jednotkového krychoidu je 4-násobně větší, tedy \(2^2\) větší. Z obázku je zjevné, že dvojnásobný krychloid můžeme sestavit z 8 jednotkových krychloidů. Objem dvojnásobného krychloidu určíme jako

\[V_2 = l_2^3\]

a bude tedy 8 dm\(^3\). Při zvětšení krychloidu na dvojnásobek délky se jeho objem zvýšil 8-krát, tedy \(2^3\). Hmotnost dvojnásobného krychloida je úměrná jeho objemu a proto se zvýšila také 8-krát (\(2^3\) krát) a bude 8 kg.

Uvažujme nyní, že krychloid dále roste a roste až nabude 10 násobku původní délky. Jeho délku můžeme napsat jako

\[l_{10}=10\,l_1\]

Jak už asi tušíme, plocha desetinásobného krychloidu se zvětší v porovnání s jednotkovým krychloidem 100 krát, tedy 10\(^2\) krát. Do objemu desetinásobného krychloidu se vejde 10x10 jednotkových krychloidů na jednu základnu a takových složení budeme mít nad sebou 10, objem se tedy zvýší 10 x 10 x 10 = 10\(^3\), tedy tisíckrát. Hmotnost krychloidu také výrazně vzroste a dosáhne 10\(^3\) násobek původní hmotnosti 1 kg. Hmotnost desetinásobného krychloidu bude 1 tuna.

Obdobným způsobem bychom mohli uvažovat o živočichovi ve tvaru koule o poloměru \(r\), který má plochu \(4\,\pi\,r^2\) a objem \(4/3\,\pi\,r^3\). Při zvýšení jeho poloměru na dvojnásobek by se jeho plocha změnila na \(4 \pi 2^2 r = 2^2 V_1\) a jeho objem by se změnil na \(4/3\,\pi\, 2^3\,r^3 = 2^3 V_1\).

Zjistili jsme tedy, že při zdvojnásobení objemu se plocha zvýší s druhou mocninou a objem se zvýší s třetí mocninou změny jeho lineárních rozměru. Tento poznatek obecně vychází z geometrie, protože vzorec pro výpočet plochy vždy obsahuje délku umocněnou na druhou a vzorec pro výpočet objemu délku umocněnou na třetí.

Těleso	Plocha	Objem
Krychle	\(6\,a^2\)	\(a^3\)
Koule	\(4 \pi r^2\)	\(\frac{4}{3}\pi r^3\)
Válec	\(2\,\pi r^2+2\,\pi\,r\,h\)	\(\pi r^2 h\)

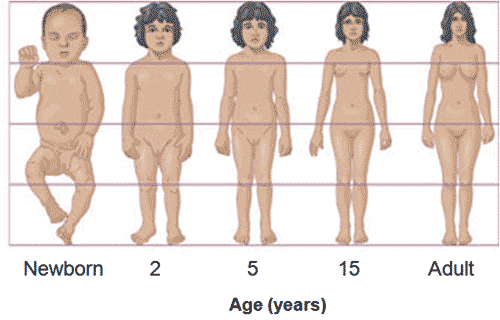
Naše zjištění tedy platí pro tzv. izometrické škálování, t.j. škálování při kterém dochází ke zvýšení lineárních rozměrů ve všech směrech. Příklad, kdy toto škálování neplatí si můžeme ukázat na příkladu válce. Představte si, že máte válec, např. konzervu tuňáka v oleji o poloměru základny \(r_1\) a výšce \(h_1\). Chcete mít větší konzervu, tak zvýšíte její výšku (např. \(h_2=2\,h_1\)), její základnu necháte nezměnénou. Jak se změní její objem? Podle vztahu v tabulce dojde k lineárnímu zvýšení (\(V_2 = \pi\,r^2 h_2 = 2 \pi\,r^2 h_1 = 2^1\,V_1\)). Tento trik využívají výrobci, kteří při zvětšování obalu nezvětšují obal izometricky, ale jenom v jednom směru, nejlépe ve směru, který je ve vzorci pro výpočet objemu v první mocnině. Výrobek tak budí dojem výrazně většího výrobku bez zvýšení jeho objemu jenž by vyžadovalo izometrické škálování. Škálování, při kterém roste jen jeden z rozměrů nebo jednotlivé rozměry výška, šířka a délka nerostou rovnoměrně označujeme jako škálování alometrické. Typickým příkladem alometrického škálování je růst člověka. V případé, že by se tělo škálovalo izometricky rostla by váha s třetí mocninou výšky. Alometrické škálovaní nebo růst znamená také to, že se v průběhu růstu mění poměry mezi jednotlivými částmi lidského těla. Můžeme to vidět v porovnání antropometrických parametrů dospělého člověka a dítěte, kde vidíme např, že déti mají například vzhledem k tělu mnohem větší hlavu.

Stejně jako geometricky jednoduché objekty a tvary, můžeme takto škálovat i složitější objekty. Jako příklad může poslužit tvar listu na obrázku.

Jeho plochu můžeme určit tak, že list natřeme barvou a otlačíme ho na milimetrový papír. Následně spočítáme všechny zabarvené čtvrce a součtem jejich ploch určíme plochu listu. Když chceme vědet, jakou plochu bude mít list dvojnásobné velikosti, představte si, že nahradíme každý z počítaných čtverců čtvercem o dvojnásobné straně. Plocha každého ze čtverců bude čtyřnásobná a tedy i celková plocha bude čtyřnásobná.

Poměr objem a plocha

Zkoumáme-li poměr mezi objemem a plochou u izometrického škálování, můžeme tuto závislot vyjádřit jednoduchým podělením plochy a objemu. Plocha k objemu je úměrná \(A/V \propto l^2/l^3 = 1/l\).[^3]. Tato závislost nám říká, že velký živočich bude mít méně povrchu vzhledem k objemu než malý živočích. Z daného pohledu je hlavním rozdílem mezi velrybou a bakterií, že bakterie má 100 000 000 krát více povrchu k objemu než má velryba.

Poměr plochy povrchu k objemu také hrál klíčovou roli v evoluci, jak poukázal Haldane [@Haldane1926]. Živý svět se skládá z buněk, které mají velmi podobné požadavky na kyslík. Mikroskopická zvířata, jako jsou například malí korýši v planktonu, pohlcují kyslík celou plochou těla a kyslík rychle difunduje do všech buněk. Pokud by se vyvinula větší zvířata ve stejném tvaru a složení těla jejich povrchová plocha by se snížila vzhledem k objemu, a tak by bylo mnohem obtížnější absorbovat dostatek kyslíku. Například hmyz používá k dýchání systém trubiček - vzdušnic otevřených průduchy na straně hrudi a zadečku. Vzduch se u hmyzu dostává přímo k vnitřním tkáním a dýchání je primárně pasivní proces. Výměna dýchacích plynů u hmyzu je tedy podmíněna difuzí, která je účinná do vzdálenosti 1 cm, takže to také omezuje velikost hmyzu.

Evoluční průlom umožňující větší velikosti zvířat přišel s rozvojem krevního oběhu jako prostředku pro distribuci kyslíku a dalších živin. I tak pro zvířata naší velikosti musí být k dispozici obrovský povrch pro absorpci kyslíku. Toho bylo dosaženo vývojem plic.

Vrátíme-li se ke korýšům, jejich trávící soustava má podobu jednoduché rovné trubky. Množství potravy, které musí přijmout vyšší zvířata je úměrné počtu buněk. Ve střevě povrch absorbuje živiny ve stejné míře a problémy vznikají proto, že plocha střevního povrchu se zvyšuje pomaleji než počet buněk, které musejí být vyživovány. Proto se v průběhu vývoje nahradila rovná trubka trubkou stočenou s mnoha vnitřnímy výběžky. Podíváme-li se na mnohé struktury vnitřní anatomie člověka, lze je chápat jako strategie, které se vyvinuly pro zvýšení disponibilní plochy povrchu zejména k výmeně dýchacích plynů a živin. To platí nejen pro živočichy ale také pro rostliny.

• V případě stromů je řešením vytvoření tenkých struktur - listů. K výměne dýchacích plynů dochází ve vnitřních strukturach listu, které jsou mnohem větší než povrch listu viditelný volným okem. Například strom, který má 2000 listů, jejich vnější plocha je přibližně 200 m\(^2\). Plocha vnitřních struktur listů je ovšem až 30 krát větší, 6000 \(m^2\), tedy 0,6 hektaru.

• U rostlin je důležité také zabezpečit co největší plochu pro příjmání živin. 1 m\(^2\) trávy má kořínky jejiž celková plocha dosahuje 350 m\(^2\).

• K výměne dýchacích plynů dochází také v našich plících. Plíce obsahují struktury alveolů s tenkou stěnou a tudíž velkým povrchem. Celková kapacita plic je přibližně 6 litrů vzduchu. Plocha, na které se tento vzduch dostává k výměne dýchacích plynů je 50 a 100 m\(^2\) co je přibližně plocha školní třídy.

• To co platilo u rostlin pro kořeny, platí pro člověka v trávicím systému. Jednotlivé klky a mikroklky navyšují celkovou plochu střeva. Celková plocha tentkého střeva, které je dlouhé přibližně 7 metrů je tak až 2000 m\(^2\).

• Kromě výměny dychacích plynů s vnějším prostředím je nutno dostat tyto dýchací plyny efektivně k jednotlivým orgánům. Proto se krevní řečišté skládá z poměrně velkých cév, které mají dostatečně velký objem k transportu a zároveň z obrovského množství tenkých kapilár, u kterých je důležitá velká povrchová plocha. Celková plocha kapilár v lidském těle je 6000 m\(^2\).

Ponderální index

Hmotnost pacienta je důležitým parametrem pro určení obezity a měření hmotnosti u jednice v průběhu času vypovídá o jeho životním stylu. Jak ale porovnáme jednotlivé pacienty mezi sebou? Jakým způsobem zjistíme, je-li váhou dvou lidí různé velikosti srovnatelná nejsou-li stejné tělesné stavby.

Při odhadu můžeme vyjít z našich znalostí škálování. Pro dva jednice stejné stavby bychom meli vydělením objemu a třetí mocniny rozměru získat konstantu. Vyšší hodnota bude odpovídat většímu objemu, než by měl být vzhledem k výšce a to může znamenat nadváhu.

Objem člověka se ovšem měří těžko, ale vzhledem k tomu, že hustota lidských tkání je přibližně stejná, je možné jako míru objemu zvolit váhu. Z lineárních rozměrů člověka je nejlépe měřitelná výška. Ta má kromě jiného tu výhodu, že se na rozdíl od jiných rozměrů nemění při nadváze. Ponderální index, označován také někdy jako Queteletův index, je tak definován jako podíl hmotnosti a třetí mocniny výšky.

Index by ovšem měl být bezrozměrný. Podíl objemu a třetí mocniny výšky získámé formálně stejné jednotky jenž má hustota kg m\(^{-3}\). Proto můžeme získat bezrozměrný index, podělíme-li ho hustotou vody \(\rho\).

\[PI = \frac{m}{\rho\,h^3}\]

V daném vyjádření je normální ponderální index v rozsahu 0,0105 až 0,014.

Tento index se používa i v jiných oblastech. Jeho modifikovaná verze je známá jako Rohrerův index stavby těla, nebo jen Rohrerův index. Rohrerův index není bezrozměrný, dosazuje hmotnost v gramech a výšku v centimetrech.

BMI - body mass index

Klasifikace	rozsah BMI(kg/m\(^2\))
Podváha	\(<18.50\)
Závažná podváha	\(<16.00\)
Střední podváha	\(16.00 - 16.99\)
Mírná podváha	\(17.00 - 18.49\)
Normální váha	\(18.50 - 24.99\)
Nadváha	\(\geq 25.00\)
Pre-obezita	\(25.00 - 29.99\)
\(27.50 - 29.99\) Obezita	\(\geq 30.00\)
Obezita 1. stupně	\(30.00 - 34.99\)
Obezita 2. stupně	\(35.00 - 39.99\)
Obezita 3. stupně	\(\geq 40.00 \)

Problémem vztahu mezi výškou a objemem se zaobíral také belgický statistik Adolphe Quetelet [@Eknoyan2008]. Ve svém díle přímo tvrdí: Quetelet toto pozorování vysvětluje tím, že člověk roste více do šírky než do výšky.

Z daného pozorování plyne zavedení indexu tělesné hmotnosti, obvykle označovaného zkratkou BMI (z anglického body mass index). Tento index vypočítáme podle vztahu

\[BMI = \frac{m}{h^2}\]

kde se hmotnost dosazuje v kilogramech a výška v metrech. Jednotkou BMI je kg m\(^-2\). Tato jednotka se většinou, a z pohledu biomechaniky nesprávně, neuvádí.

BMI se používá jako indikátor podváhy, normální tělesné hmotnosti, nadváhy a obezity, umožňující statistické porovnávání tělesné hmotnosti lidí s různou výškou. BMI jako parametr pro hodnocení obezity není vhodný při izometrickém škálování. Představme si zdravého člověka s výškou 170 cm a BMI 22 kg/m\(^2\). Kdyby byl daný člověk o 10% zvětšen, pořád mu zůstane stejná stavba těla, ale jeho hmotnost se výrazně zvýší a tím pádem se dotane do kategorie lidí s nadváhou podle BMI. BMI tak předpokládá, že vysokí lidi budou štíhlí, zatímco u lidí s nižší výškou BMI toleruje relativně vyšší hmotnost.

Dalším nedostatkem BMI pro hodnocení obezity je, že tato míra nebere do úvahy množství tělesného tuku. Příkladem mohou být sportovci s velkým množstvím svalové hmoty, kteří podle BMI spadají do oblasti obezity. Pro hodnocení obezity se proto používají i jiné míry jako je poměr obvodu pasu a boků (WHR) nebo poměr mezi obvodem pasu a výškou (WHtR). Výhodou BMI je jeho oblíbenost, při určování zdravotních rizik je BMI uvedeno u většiny studií.

Kvantifikace velikosti

Zatím jsme mluvily o délce a objemu v obecných termínech. Jakou velikost bychom měli měřit. Na výběr máme několik rozměru: délku, šírku, obvod, poloměr, průměr. Stejně tak u plochy můžeme určovat celkovou plochu nebo plochu přůřezu. Výjdeme-li z principu měření, je základem měření vzájmené porovnání.

Nejjdednodušší je to pro určení objemu. Objem těla je jenom jeden a můžeme ho relativně jednoduše odhadnout na základě hmotnosti, protože hustota těla živočichů je přibližně stejná.

Z toho, že známe objem, můžeme vyjít při určení délky. Na základě pravidel škálování je objem úměrný třetí mocnině délky. Můžeme tak třetí odmocninu délky označit jako tzv. nominální délku. Nominální délka nemusí odpovídat žádnému z rozměrů organizmů. Proto můžeme pro porovnání určit tzv. charaketristickou délku.[^5]. Charakteristická délka nám neumožní porovnat živočichy různé konstituce (např. o kolik musí bý větší krychle aby byla větší než koule). Je však použitelná, chceme-li srovnat živočichy stejného tvaru (velikost dvou brouků), nebo tvar je irelevantní zrovnáme-li živočichy jejíchž rozměry se řádově liší (bakterie a velryba). Pro geometricky podobné živočichy se veškeré délky proporcionálně mění - zdvojnásobíme poloměr, zdvojnásobí se průměr a obvod.

Linearizace grafu

Vraťme se k našemu krychloidu. Představte si, že všechny živé organizmy na planetě Krychle mají tvar krychle. Známe jejich charakteristickou délku, plochu a hmotnost, která odpovídá objemu. Jak určíme závislosti mezi délkou a plochou nebo objemem, které jsme si teoreticky odvodili v předchozí části. Na rozdíl od výpočtu můžeme využít znázornění ve grafu.

Představte si, že vezmeme data jednotlivých živočichů, jejich délku a jejich plochu a vyneseme je do grafu. Výsledkem bude množina bodů definujících křivku, v našem případě parabola. Tento graf nám ovšem neposkytne moc informací jak se plocha mění s délkou. Z grafu bychom rádi získali jednu informaci (jedno číslo), které nám určí tuto závislost.

Delší nevýhodou daného grafu je jeho rozlišení. Rozměry živočichů pokrývají různou škálu: od mikrometrů až po desítky metrů. Na světě je ovšem mnohem větší počet druhů malých živočichů o rozměrech milimetrů, než velkých o rozměrech metrů. Proto bude mít graf velké množství bodů na začátku a malé množství bodů na konci rozsahu velikosti.

Ukážeme si, jak můžeme vyřešit oba tyto problémy najednou, jednoduchým změněním vynášení dat na jednotlivé osy. Místo vynášení jednotlivých hodnot na osy grafu v lineárním měřítku budeme na jednotlivé osy vynášet v tzv. logratimickém měřítku. Znamená to, že vzdálenosti na ose nebude odpovídat skutečným poměrem velikostí ale násobku vzdálenosti, t.j. vzdálenost mezi 1 a 10 bude stejná jako vzdálenost mezi 100 a 10000. Stejně tak bude platit, že vzdálenost mezi 1 a 3 bude stejná jako vzdálenost 3 a 9 a vzdálenost mezi 9 a 27. Stejně to platí na druhou stranu, vzdálenost mezi 0.1 a 0.01 je stejná jako vzdálenost mezi 0 a 1. Co se stane s grafem, uděláme-li danou změnu. Pro označení os v tomto grafu použijeme označení \(x', y'\).

Představme si tři živočichy, kteří mají charakteristický rozměr (\(l\)) 0.1 m, 1 m a 10 m. Jejich plocha se mění přesně podle zákona škálování a to v poměru \(A=l^2\), t.j. mají plochu 0.01, 1 a 100. Jáké budou vzdálenosti na ose linearizovaného grafu \(\mathrm{log}\,l\) a \(\mathrm{log}\,A\). Z definice zavedení logaritmu je zřejmé, že vzdálenosti na ose \(\mathrm{log} l\) jsou stejné. Na ose \(\mathrm{log}\, A\) je vzdálenost mezi 1 a 10 stejná jako mezi 10 a 100, t.j. vzdálenost mezi 1 a 100 se rovná dvěma jednotkám vynášené vzdálenosti. Stejně to platí pro pro vzdálenosti mezi 0 a 0,01. Výsledkem tedy bude lineární graf, kde pro jeden přírustek na ose \(\mathrm{log}\, l\) máme dva přírůstky na ose \(\mathrm{log}\, A\).

Původní graf, který měl lineární osy, byl vhodný pro kreslení funkcí ve tvaru $\(y = ax + b\,\,.\)$

Grafem této funkce je přímka a přímo z grafu můžeme vyčíst parametry přímky. Bod na ose \(y\), který protíná přímka se rovná parametru \(b\). Parameter \(a\), označovaný jako směrnice přímky, udává sklon přímky. Funkce s vyšší hodnotou \(a\) jsou strmější než ty, které mají malou hodnotu \(a\). Můžeme ho přímo z grafu určit odměřením úhlu \(\alpha\), který zvírá naše funkce s osou \(x\); \(a=\tan(\alpha)\). Jinými slovy, je sklon křivky \(a\) mírou toho nakolik při změne \(x\) roste hodnota \(y\); \(a\) změna \(x\) = změna \(y\).

\[a\,\Delta x = \Delta y\]

V nově změneném grafu \(x'y'\) jsme vyřešili problém velikosti živočichů. Hmyzu, který má velikosti od mm (10\(^{-3}\) m) do centrimetrů (10\(^{-2}\) m), přináleží v grafu stejný rozsah os jako velkým savcům v rozměrech jednoho (\(10^0\) m) metru až několika metrů (10\(^{1}\) m).

Co ovšem znamená sklon grafu? Předpokládejme, že máme graf ve změněných osách ve tvaru přímky \(y' = a x'\), ve kterém na jednu jednotku přírustku na ose \(x'\) připadají dvě jednotky přírustku na ose \(y'\). Osa \(y'\) ovšem není lineární, to znamená, že rozdílu mezi jednotkovou vzdálenost na ose \(x\) mezi 1 a 10 odpovídají dva jednotky na ose \(y\), t.j. rozdíl mezi 1 a 100 (10\(^2\)). Máme-li na ose \(x\) číslo 3, musí ji na ose \(y\) náležet číslo, které je dvojnásobně tak daleko, t.j. číslo 9 (3\(^2\)). Kdybychom měli sklon 3, t.j. na jednu jednotku na ose \(x'\) by připadaly tři jednotky na ose \(y'\), znamenalo by to, že intervalu mezi 1 a 10 odpovídá interval mezi 1 a 1000 (10\(^3\)). Sklon křivky v grafu \(x'y'\) tak odpovída exponentu mocniny v grafu s lineárními osami \(xy\). $\(y = x^a\)$ Zvolíme-li tento způsob vykreslení, z křivky, která byla exponenciální (parabola) se stane křivka lineární, u které můžeme jednoduše určit jednotlivé parametery. Tento postup se označuje jako linearizace grafu a umožní nám jednoduchým způsobem určování vztahů mezi veličinami, mezi kterými je mocninový vztah.

\(y\)	\(a\)	\(b\)
Plocha těla 1.95	0.11
Hmotnost kostí (suchozemští)	3.25	0.0608
Hmotnost kostí (vodní)	3.07	0.137
Hmotnost svalů	3.00	0.45
Metabolická spotřeba	2.25	4.10
Efektivní objem plic	3.09	0.0000567
Frekvence dýchání	-0.78	0.892
Hmotnost srdce	2.94	0.0058
Frekvence tepu	-0.75	4.02
Hmotnost ledvin	2.55	0.00732
Hmotnost jater	2.61	0.033
Hmotnost mozgu (neprimáti)	2.10	0.01
Hmotnost mozgu (člověk)	1.98	0.085

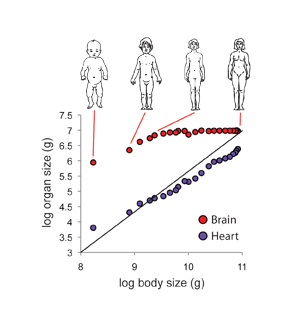
Hodnotu \(a\) můžeme určit jednoduše z grafu tím, že určíme směrnici logaritmického grafu, \(a\) změna \(x'\) = změna \(y'\). Máme-li kalkulačku, která umí počítat logaritmy můžeme to jednoduše určit jako

\[a = \frac{\Delta \log y}{\Delta \log x}\]

Samozřejmě ani přímka linearizovaného grafu nemusí procházet nulou. V případě linarizovaného grafu \(b\) závisí na volbě jednotek. Kdybychom například místo metrů používaly pro vynášení milimetry, všechny hodnoty jsou vynásobené parametrem 1000. Znamená to, že místo 1 budeme omít 1000 a místo 10 budeme mít 10 000. V linearizovaném grafu se 1 posune o tři jednotky doprava a 10 a čtyři jednotky doprava. Přímka grafu se tak celá posune o tři jednotky doprava. Posun o \(b =\) tři jednotky znamená, že jsme násobili \(10^3\). Hodnotu \(b\) můžeme z grafu vyčíst jako hodnotu \(y'\) při \(x\) rovné jedné, protože \(1^a\) se rovná jedné pro libovolné \(a\).

Pro nás je zejména důležité znát faktor škálování \(a\). Protože živočichové na zemi a ani člověk nemá právě tvar krychle, faktor škálování nemusí být přěsně 3. Nejjednodušší způsob, jak tuto hodnotu získat je právě graficky, kde do logaritmického grafu budeme vynášet na vodorovnou osu charakteristickou délku (např. výšku člověka) a na svislou osu vyneseme hmotnost, případně jiný parametr.

Koeficienty škálování pro jednotlivé parametry lidského těla jsou uvedeny v tabulce. Je zajímavé, že hmota kostí roste rychleji než celková hmota organizmu, zatímco metabolická spotřeba celkově roste, ale ne tak rychle jako hmotnost. Tudíž větší živočichové mají menší spotřebu energie na kilogram hmotnosti. Tomuto fenomenu se budeme ještě věnovat.

Škálování a Gallileo

Galileo Galilei byl prvním, kto popsal podstatu škálování [@Shingleton2010] tak, jak jsme si jí vysvětlili v předcházejícím textu. K danému poznání ho přivedlo kromě jiného jednoduché porovnání pevnosti kostry zvířat. Galileo začíná své dílo Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze (stručně překládáno jako ) porovnáním pevnosti lodí různé konstrukce. Ptá se, proč musí mít větší loď více výstuh než malá, když je přímo její zvětšením. Galileo pozoruje, že daná závislost neplatí jen pro lodě ale také pro zvířata a přímo se ptá:

Všichni vědí, že kůň si při pádu z výšky tří nebo čtyř loktů (1,3 m nebo 1,8 m) zlomí kosti , zatímco pes padající ze stejné výšky neba kočka padající z výšky osmi až desíti loktů neutrpí žádnou újmu? … A nejen menší zvířata jsou poměrně silnější a robustnější než větší, taky i menší rostliny jsou schopny vydržet víc. Oba víme, že dub dvěstě loktů vysoký (9 m) neudrží své vlastní větve když bude tvar jeho koruny stejný jako u stromu běžné velikosti; a že příroda nemůže vytvořit koně stejně velké jako dvacet obyčejných koní nebo obry desetkrát vyšší než obyčejný člověk, pokud by se zázrakem nezměnily proporce jejich končetin a zejména jejich kostí, které by musely být silnější než je obvyklé.

Galileo si také všímá, že kosti jednotlivých zvířat nejsou úměrné jejich velikosti. Na obrázku je znázorněna kostra kočky a slona.

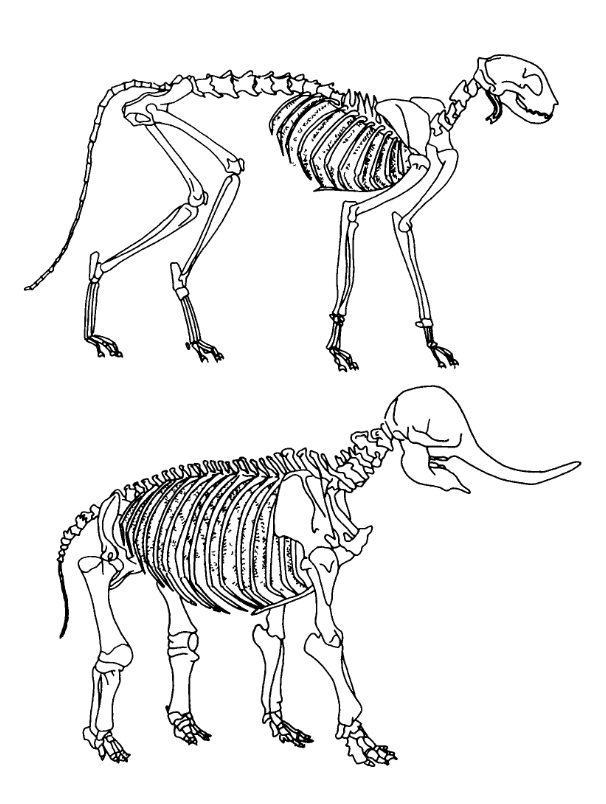
I když jsou oba kostry na obrázku stejné velikosti, můžeme je lehce rozlišit na základě tloušťky kostí. Slon má vzhledem ke své velikosti mnohem větší kosti. Je zřejmé, že tato vlastnost bude souviset se zákonem třetí mocniny, který jsme si odvodili pro škálování.

Představte si drátěnné lano, na kterém je zavěsen výtah. Drátěné lano je druh lana, které je vyrobeno z několika kovových vláken. Pevnost lana je úměrná tomu, kolik je v průřezu lana kovových vláken, čím je větší průřez, tím je v něm více vláken a tím lano unese větší váhu. Jak se musí změnit průměr lana, když kabinu výtahu zvětšíme dvakrát (\(l=2 l_0\)). Víme, že na mezi lineárním rozměrem a hmotností platí zákon třetí mocniny a tudíž bude kabina vážit třikrát tolik (\(m = 8 m_0\)). Proto musí být lano 8-krát silnější a tedy jeho plocha průřezu musí být osminásobkem původní plochy průřezu. Má-li průřez lana tvar kruhu musí pro poloměr platit: $\(A = 8 A_0\)\( \)\(\pi r^2 = 8 \pi r_0^2\)\( \)\(r = 2^\frac{3}{2} r_0\)$ Poloměr lana, což je mírou jeho lineárního rozměru tedy roste víc než lineární rozměr výtahu. Budeme-li pořád zvětšovat rozměr kabiny, dostaneme se do bodu, kdy průměr lana bude větší než samotná kabina a lano bude vážit tolik, že neunese vlastní váhu.

Vztah mezi pevností v tahu nebo tlaku a průřezem platí obecně a ne jenom pro drátěné lano. Stejně tak pevnost kostí v tlaku je úměrná jejich ploše průřezu. Můžeme tuto závislost vyjádřit vztahem pro maximální sílu, která je pro danou kost úměrná průřezu: $\(F_{max}=\sigma_P A\)\( kde \)\sigma_P\( je koeficient úměrnosti a označuje se jako mez pevnosti. Tato mez je charakteristická pro každý materiál a pro kortikální kost má hodnotu přibližně 200 N/mm\)^2$.

Představme si živočicha, který bude mít tvar krychle o straně \(l\) a bude mít jednu kost čtvercového průřezu o straně \(a\). Dále předpokládejmě, že hustota kosti je dva krát větší než hustota běžné tkáně. Pro hmotnost živočicha tedy platí $\(m = \rho (l^3-a^2 l) + 2 \rho a^2 l = \rho l^3 + \rho a^2 l\)$ Unese-li kost přesně tíhu živočicha, musí platit

\[F_{max} = m g = \sigma_P a^2\]

Proto

\[a^2 = \frac{l^3}{\frac{\sigma_P}{\rho g}- l}\]

To kolik kostní hmoty potřebuje živočich musí záviset na jeho hmotnosti. Vyjádřeme si poměr mezi objemem kostí (\(V_{\mathrm{kost}}\)) a objemem živočicha (\(V\)) jako

\[x = \frac{V_{\mathrm{kost}}}{V} = \frac{a^2}{l^2}\]

kde \(A_{\mathrm{kost}}\) je plocha kosti.

\[\frac{m_\mathrm{kost}}{m} = \frac{2\rho V_\mathrm{kost}}{V} = 2 \frac{l}{\frac{\sigma_P}{\rho g}- l}\]

Z daného vztahu vidíme, že tento poměr není konstatní a závisí na velikosti \(l\). Je-li hustota \(\rho\) stejná jako hustota vody (1000 kg/m\(^3\)) a gravitační zrychlení je približně 10 m/s\(^2\), můžeme pro mez pevnosti 200 N/mm\(^2\) napsat:

\[\frac{m_\mathrm{kost}}{m} = \frac{l}{10^4 [\mathrm{m}] - l}\]

Protože hmotnost je při izometrickém škálování funkcí třetí mocniny délky \(m \propto l^3\), měla by se hmotnost kostry při zachování stálé pevnosti škálovat se čtvrtou mocninou lineárního rozměru. Podle tabulky  se hmotnost kosti zvyšuje více než celková hmotnost (koeficient \(a=3\)), nicméně méně než s čtvrtou mocninou. To znamená, že větší živočichové mají hrubší kosti a ne natolik, jak by potřebovali pro dosažení stejné mechanické odolnosti jako mají malí živočichové. A tím se vracíme k pozorování Galilea o pádu koně z 1.5 metru.

Škálování a energetická spotřeba

Může se zdát, že velikost těla je nevýhodou, protože s rostoucí délkou a hmotností rostou požadavky na pevnost kostí. Na druhé straně, může být velká hmotnost, resp. velký poměr objemu těla k povrchu výhodou. Při relativně menším povrchu těla je výhodnější udržet konstantní tělesnou teplotu, což má několik výhod. Například je možné nastavit biochemické pochody tak, aby fungovaly optimálně při dané teplotě. Také činnost svalů je efektivnější když fungují jenom v úzkém rozsahu teplot.

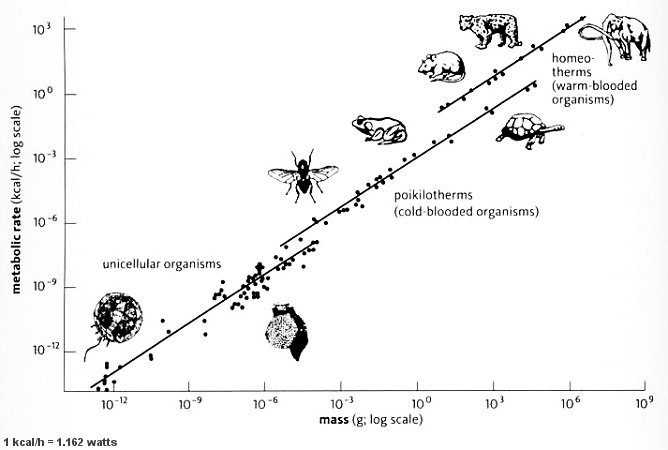
Udržování tělesné teploty je metabolicky náročné. Pro dospělého člověka je to až kilogram potravin denně. Myš, která má rozměr asi jedné dvacetiny rozměru člověka, má asi větší plochu a musí spotřebovat až dvacetkrát tolik jídla jako člověk, samozřejmě přepočteno na hmotnost myší. Myš tedy musí spotřebovat čtvrtinu své vlastní tělesné hmotnosti denně jen aby zůstala v teple. To je důvod, proč v arktických oblastech Špicberků je nejmenším savcem liška. Tato úměra platí i na druhou stranu. Kdyby měla kráva metabolizmus stejně rychlý jako myš, teplota uvnitř jejího těla by přesáhla bod varu. Vztah, který říká, že energetická spotřeba živočicha neroste úměrně s jeho hmotností se označuje jako Kleiberův zákon.

Na základě této úvahy můžeme vysvetlit také alometrický růst dětí, nebo obecně teplokrevních živočichů. Plazi a ryby nejsou nuceni udržovat zvýšenou teplotu, takže je tepelné ztráty netrápí. Ale savci a ptáci musí udržovat svou zvýšenou teplotu přes svůj život, jak rostou ve velikosti od dítěte k dospělému. Vzhledem k tomu, že rostou ve velikosti, tyto obratlovci začínají život s tělěm, které má relativně vysoký poměr povrchu k objemu.

U dětí znamená jejich malá hmotnost to, že vzhledem k relativně velkému povrchu rychle ztrácí teplo. Proto mají děti problém udržet stálou tělesnou teplotu. Pro zvládnutí této nevýhody došlo u mláďat savců k několika adaptacím. Teplokrevné nebo endotermické děti musí být při narození mnohem větší, než mláďata chladnokrevných ektotermických plazů. Větší velikost každého narozeného jednotlivce znamená méně potomků z každého období těhotenství endotermické obratlovců. Tak zatímco každý savčí období těhotenství přivede na svět jednoho až deset potomků, typický plazí období těhotenství povede k narození zhruba desti až sta potomků. Problém splnění minimální velikosti potřebné k udržení konstantní tělesné teploty je zvláště akutní pro nejmenší teplokrevní obratlovce. Nově narozených netopýr může mít až 25% hmotnosti dospělé matky.

Dalším přizpůsobením endotermických obratlovců je, že teplokrevné děti nerostou úměrně od dítěte k dospělému. Jinými slovy, zatímco plazi se jeví jako miniaturní dospělí většina mláďat savců nemůže být zaměněna za dospělého. Endotermické děti mají menší plochu, t.j. kratší končetiny, zaoblené rysy a kulatou hlavu. Tyto úpravy pomáhají teplokrevným dětem snížit tepelné ztráty povrchem a udržet konstantní zvýšenou tělesnou teplotu.

Význam udržení stálé tělesné teploty můžeme doložit na základě pravidel přežití. Člověk může přežít tři týdny bez jídla, nebo tři dny bez vody, ale v případě, že nemá dostatečnou izolaci od chladu může být mrtvý do tří hodin. Fyzika a měřítka vlastností jsou základem pro pochopení většiny pozorování v biologie a medicíně.

Kleiberův zákon

Kleiberův zákon je biologický princip, který popisuje vztah mezi bazálním metabolismem (minimálním množstvím energie, které organismus potřebuje k přežití) a tělesnou hmotností. Zákon říká, že metabolismus není přímo úměrný hmotnosti organismu, ale spíše roste s mocninou hmotnosti.

\[Q \propto m^{3/4}\]

kde:

• \(Q\) je bazální metabolická rychlost organismu (měřená v jednotkách energie za jednotku času, např. watty).

• \(M\) je tělesná hmotnost (měřená v kilogramech).

Konstanta úměrnosti a se liší podle skupiny organismů (např. savci, ptáci, rostliny), ale exponent 3/4 (nebo 0,75) je překvapivě konstantní napříč širokým spektrem živých organismů.

Hlavní myšlenka Kleiberova zákona spočívá v tom, že ačkoliv větší zvířata potřebují více energie celkově, spotřebovávají méně energie na každý kilogram své hmotnosti než zvířata menší.

Představme si slona a myš. Pro zjednodušení předpokládejme, že slon má hmotnost 5800 kg a myš 58 g (což je 0,058 kg). Hmotnost slona je tedy přibližně 100 000krát větší než hmotnost myši.

Podle Kleiberova zákona se jejich bazální metabolismus neřídí tímto poměrem 1:100 000, ale roste s mocninou \(3/4\).

1. Hmotnostní poměr (lineární): \(M_{slon} / M_{myš} \approx 100\,000\)

2. Metabolický poměr (podle Kleiberova zákona): Poměr metabolických rychlostí je dán poměrem hmotností umocněným na \(3/4\). \(Q_{0, slon} / Q_{0, myš} \approx (100\,000)^{3/4}\)

   Vypočítáním zjistíme, že \((100\,000)^{3/4}\) je přibližně \(10\,000\).

To znamená, že ačkoli je slon 100 000krát těžší než myš, jeho celkový metabolismus je jen asi 10 000krát vyšší.

Tento rozdíl je ještě markantnější, když se podíváme na spotřebu energie na jeden kilogram tělesné hmotnosti.

• Slon má metabolismus 10 000x větší a hmotnost 100 000x větší. Z toho vyplývá, že na každý kilogram své hmotnosti spotřebuje 10krát méně energie než myš.

• Myš má naopak velmi rychlý metabolismus. Na každý kilogram svého těla potřebuje mnohem více energie, aby si udržela stálou tělesnou teplotu a základní životní funkce. Proto myši potřebují jíst téměř nepřetržitě, zatímco velká zvířata mohou jíst méně často.

Kleiberův zákon ukazuje, že bazální metabolismus velkých živočichů je sice vyšší než u malých, ale ne proporčně. To znamená, že menší zvířata spotřebovávají relativně více energie na jednotku hmotnosti. Tento jev má dalekosáhlé důsledky v biologii, od vysvětlení rozdílů v srdeční frekvenci a délce života po fungování ekosystémů.

Opakování

• Izometrický růst: rovnoměrné zvýšení všech rozměrů ve stejném poměru.

• Alometrický růst: nerovnoměrné zvyšování jednotlivých rozměrů.

• Podíl plochy k objemu je nepřímo úměrný délce. \(\frac{S}{V} \propto l^{-1}\)

• Nominální délka: třetí odmocnina objemu živočicha

• Charakteristická délka: fyzikální rozměr živočicha

• Logaritmus: je matematická operace, která udává kolikrát musíme násobit určité číslo označované jako báze sebou samým proto, aby jsme dostali jiné číslo. Např. logaritmus 100 s bází 10 se rovná 2 (\(\log_{10} 100 = 2\)), protože 10 musíme mezi sebou vynásobit 2-krát (\(10\,10=100\)). Kůli jednoduchosti označujeme dekadický logaritmus \(\log_{10}\) jen jako \(\log\).

• Kleiberův zákon uvádí, že rychlost metabolismu zvířete je úměrná ohybuje 3/4 organizmu.