Síly v biomechanice

V biomechanice se síly působící na tělo dělí na dvě základní kategorie: externí a interní síly.

Externí síly (vnější síly)

Externí síly jsou ty, které působí na tělo z okolního prostředí. Mají významný vliv na rovnováhu, stabilitu a pohyb těla.

Gravitační síla (\(\vec{F}_g\))

Gravitační síla (tíhová síla), kterou Země přitahuje tělo k sobě.

\[ \vec{F}_g = \vec{m} \cdot g \]

kde \(m\) je hmotnost těla a \(g\) gravitační zrychlení (přibližně 9.81 m/s²). Značí se také \(\vec{W}\).

Charakteristika	Popis
Působiště	těžiště
Velikost	\(F_G = m \cdot g\)
Směr	směrem do středu Země, směrem dolů
Nositelka	těžnice

Warning

Hmotnost není tíha

• Hmotnost je fyzikální veličina, která vyjadřuje množství látky v tělese. Je to skalární veličina a její hodnota je vždy stejná, nezávisle na tom, kde se těleso nachází (na Zemi, Měsíci nebo ve ve vesmíru).

• Tíha je síla, kterou působí Země (nebo jiné gravitační těleso) na objekt. Na rozdíl od hmotnosti závisí na gravitačním poli, ve kterém se těleso nachází. Je to vektorová veličina – má tedy velikost i směr.

Vlastnost	Hmotnost (m)	Tíha (FG)
Definice	Množství látky v tělese	Síla působící na těleso v gravitačním poli
Jednotka	Kilogram (kg)	Newton (N)
Typ veličiny	Skalární	Vektorová (má směr)
Závislost na poloze	Nemění se	Závisí na gravitačním poli
Příklad	Hmotnost 70 kg na Zemi i na Měsíci	Tíha na Zemi ≈ 686 N, na Měsíci ≈ 114 N

from IPython.display import IFrame
IFrame('https://www.geogebra.org/classic/KDav5HcX', width=800, height=600, style="border: 1px solid black")

Reakční síla podložky (Ground Reaction Force - GRF)

Reakční síla podložky je síla, kterou podložka působí na těleso stojící nebo pohybující se na jejím povrchu. Tato síla je důsledkem třetího Newtonova zákona akce a reakce – každá akce vyvolává stejně velkou, ale opačně orientovanou reakci.

:width:200px

Reakční síla podložky má dvě složky:

1. Normálovou složku \(F_N\) – kolmá k povrchu podložky.

2. Tečnou složku \(F_T\) – rovnoběžná s povrchem podložky a často spojovaná s třením.

Rozklad reakční síly na složky

Celkovou reakční sílu podložky \(\vec{F}_R\) můžeme rozložit na dvě základní složky:

\[ \vec{F}_R = \vec{F}_N + \vec{F}_T \]

• Normálová složka (\(F_N\))

  • Směřuje kolmo k podložce.

  • Vyrovnává tíhu tělesa a zabraňuje jeho proniknutí do podložky.

  • Při statické rovnováze platí:

  • \[ F_N = F_G = m \cdot g \]

  • Pokud je těleso v klidu, je normálová síla rovna tíze tělesa.

    Charakteristika	Popis
    Působiště	težiště tlaků
    Velikost	určuje se výpočtem
    Směr	kolmo na podložku proti možnému posuvu
    Nositelka	kolmice na podložku

• Tečná složka (\(F_T\))

  • Leží v rovině podložky a souvisí s třením.

  • Odpovídá za odpor vůči pohybu tělesa po podložce.

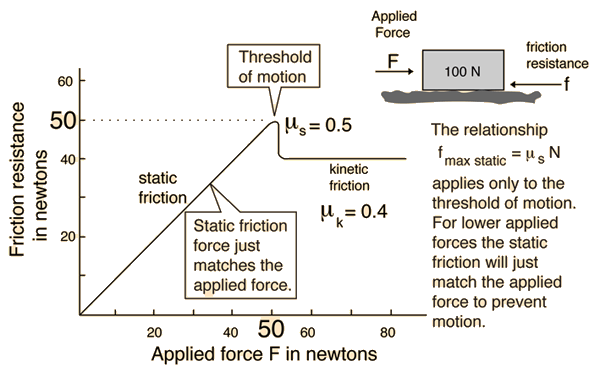
  • Maximální hodnota tečné složky se řídí Coulombovým zákonem tření:

    \[ F_T \leq \mu \cdot F_N \]

    kde \(\mu\) je součinitel tření (statického nebo dynamického).

    Charakteristika	Popis
    Působiště	težiště smykových napětí
    Velikost	určuje se výpočtem
    Směr	rovnoběžně s podložkou
    Nositelka	kolmice na podložku

Tlak \(p\)

Tlak je fyzikální veličina vyjadřující sílu působící na jednotku plochy. Udává, jak velká síla působí na určitou plochu kolmo k jejímu povrchu.

• Značka: \(p\)

• Jednotka: pascal (Pa) = N/m\(^2\)

• Vztah:

  \[ p = \frac{F_N}{A} \]

  kde:

  • \(F_N\) je normálová síla (v N),

  • \(A\) je plocha kontaktu (v m²).

Osoba s hmotností 70 kg stojí na podložce:

• Normálová síla:

  \[ F_N = 70 \, \text{kg} \cdot 9.81 \, \text{m/s}^2 = 686.7 \, \text{N} \]

• Plocha chodidel: Předpokládejme, že celková plocha chodidel je 0,03 m\(^2\).

• Výpočet tlaku:

  \[ p = \frac{686.7 \, \text{N}}{0.03 \, \text{m}^2} = 22,890 \, \text{Pa} \, (\text{≈ 22.9 kPa}) \]

Veličina	Symbol	Jednotka	Význam
Normálová síla	\(F_N\)	N	Síla působící kolmo na povrch
Kontaktní plocha	\(A\)	m²	Plocha, na kterou působí síla
Tlak	\(p\)	Pa (N/m\(^2\))	Síla působící na jednotku plochy

Při nerovnoměrném rozdělení tlaku můžeme určit místo působení kontaktní síly jako:

Center of Pressure (COP) – těžiště tlaků

Center of Pressure (COP) je bod na povrchu podložky, ve kterém by měla být soustředěna výslednice všech tlakových sil působících mezi tělesem a podložkou, aby vyvolala stejný moment jako skutečné rozložení tlaků.

• COP je bod působení výsledné reakční síly podložky.

• Při udržování rovnováhy se COP neustále mění kvůli drobným pohybům těla (tzv. posturální kyv).

• Pro udržení rovnováhy musí být COP udržováno v rámci základny opory (BOS).

• \(F_{N}\) jako reakční sílu podložky,

• \(x_i, y_i\) jako souřadnice jednotlivých tlakových bodů,

• \(F_i\) jako sílu působící v každém bodě,

pak souřadnice COP (\(x_{COP}, y_{COP}\)) lze vyjádřit jako:

\[ x_{COP} = \frac{\sum_{i} x_i F_i}{\sum_{i} F_i} \]

\[ y_{COP} = \frac{\sum_{i} y_i F_i}{\sum_{i} F_i} \]

• Pokud je člověk v klidu a stabilní, COP je blízko projekce těžiště (COG) na podložku.

• Při pohybu (např. při chůzi) se COP dynamicky přesouvá podle rozložení hmotnosti a tlaku.

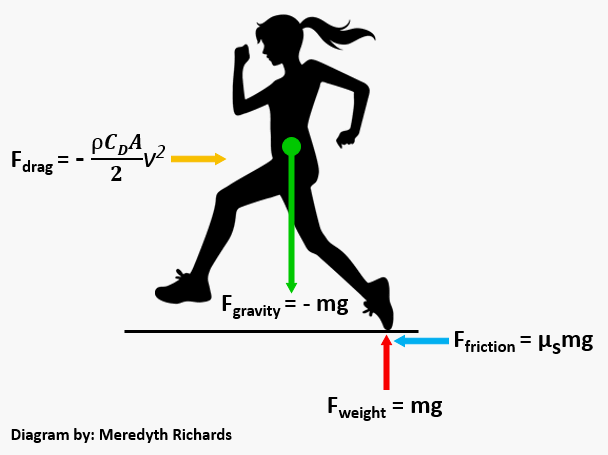
Odporové síly

• Tření (\(\vec{\mathbf{F}}_t\)): Tření je síla, která vzniká mezi dvěma povrchy, které se dotýkají a pohybují proti sobě nebo se snaží o pohyb. Tření vždy působí proti směru pohybu nebo proti směru snahy o pohyb.

  • Statické tření (\(\vec{\mathbf{F}}_{ts}\)): Působí mezi tělesy, která jsou v klidu a brání jim v pohybu.

    \[ F_{ts} \leq \mu_s N\]

    kde \(\mu_s\) je koeficient statického tření a \(N\) je normálová síla.

  • Kinetické tření (\(\vec{\mathbf{F}}_{td}\)): Působí mezi tělesy, která se pohybují proti sobě.

    \[ F_{tk} \leq \mu_k N\]

    kde \(\mu_k\) je koeficient kinetického tření a \(N\) je normálová síla.

• Odpor prostředí (\(\vec{\mathbf{F}}_o\)): Odpor prostředí (např. odpor vzduchu nebo odpor kapaliny) je síla, která působí proti pohybu tělesa v daném prostředí. Velikost odporu prostředí závisí na rychlosti tělesa a na vlastnostech prostředí.

  • Odpor vzduchu (pro nízké rychlosti):

    \[F_o = -b v\]

    kde \(b\) je konstanta odporu prostředí a \(v\) je rychlost tělesa pro malé hodnoty Reynoldsova čísla.

  • Odpor vzduchu (pro vysoké rychlosti):

    \[F_o = -1/2 \rho C_d A v^2\]

    kde \(\rho\) je hustota prostředí, \(C_d\) je součinitel odporu, \(A\) je plocha tělesa a \(v\) je rychlost tělesa.

Tip

Vysvětlení odporu podle NASA

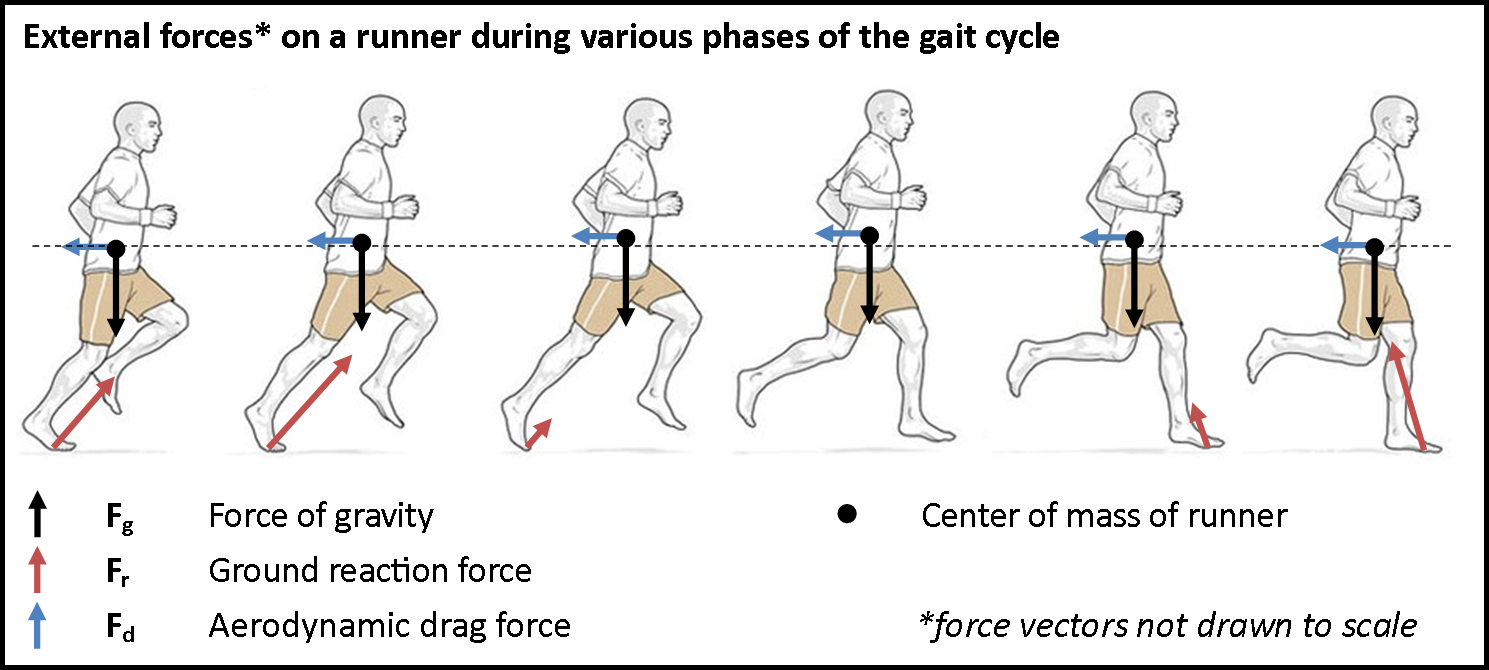
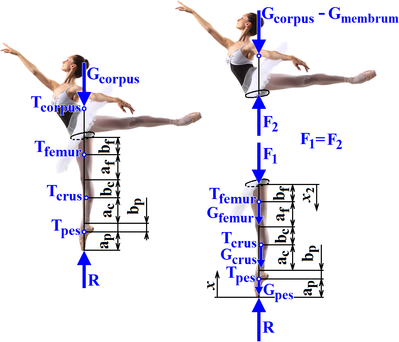
Interní síly (vnitřní síly)

Interní síly vznikají uvnitř těla a jsou generovány svalovou kontrakcí, napětím vazů nebo reakcemi mezi kostmi. Tyto síly neovlivňují pohyb těla jako celku, ale jsou klíčové pro udržení stability a vnitřní rovnováhy.

Typy interních sil:

• Svalové síly – síly generované kontrakcí svalů, které umožňují pohyb a stabilizaci kloubů.

• Síly působící mezi kostmi – například kompresní síly v kloubech při zatížení.

• Napětí vazů a šlach – pasivní síly, které stabilizují klouby a omezují nadměrný pohyb.

• Intraabdominální tlak – tlak v dutině břišní, který pomáhá stabilizovat páteř při zátěži.

Srovnání externích a interních sil

Typ síly	Externí síly	Interní síly
Původ	Působí z okolního prostředí	Vznikají uvnitř těla
Příklady	Gravitační síla, tření, reakce podložky	Svalová kontrakce, napětí vazů
Účel	Pohyb těla jako celku, rovnováha	Stabilizace kloubů, řízení pohybu
Měřitelnost	Lze měřit přímo (např. silovou plošinou)	Obtížně měřitelné, často odhadované modelem