Těžiště

Těžiště#

Lidské tělo se skládá z buněk, ty se skládají z molekul a ty z atomů. Každý z atomů lidského těla má svou hmotnost a součet hmotností všech částí lidského těla je celkové hmotnosti. Představte si, že by jste měli psát rovnici rovnováhy, která by obsahovala členy odpovídající gravitačním sílám všech atomů v lidském těle. Tato rovnice by měla 7,10\(^{27}\) členů, co je podstatně víc než je člověk za svého života schopen napsat.

Proto musíme pro výpočet rovnováhy přijmout zjednodušení, které nám umožní řešit dané problémy. Představte si jednoduché těleso o tíze 10~N na dvou podpěrách. V každé z podpěr budeme mít umístněný silový snímač. Tyto podpěry můžeme umístnít tak, že na každou z podpěr bude působit stejná síla, t.j. 5~N. Následně uvažujme, že dané podpěry budeme posouvat k sobě přičemž pořád na každé z nich měříme stejnou sílu. V jeden okamžik se nám podpěry navzájem dotknou a v daném místě pozoruje celou tíhu tělesa. To místo je charakteristické tím, že při podepření v něm působí celá tíha tělesa a označujeme ho jako těžiště.

Stejně tak jako určení těžiště tělesa, můžeme určit těžiště lidského těla. Těžiště těla tedy můžeme označit jako bod, vůči kterému jsou momenty gravitačních sil působících na hmotu tělesa rovné nule. Tato definice nám tedy určuje to, že momenty jednotlivých segmentů lidského těla jsou vůči těžišti v rovnováze. Neznamená to, že hmotnosti segmentů těla (nebo tíhy) jsou vůči těžišti rozděleny rovnoměrně.

Znalost bodu těžiště v biomechanice je důležita, protože těžiště má určité speciální vlastnosti:

  • Z mechanického hlediska můžeme na těžiště nahlížet jako na bod, ve kterém je koncentorvána veškerá hmotnost člověka. Letí-li lidské těla jako projektil, opisuje těžiště těla parabolickou trajektorii, bez ohledu na to jak se pohybují jednotlivé segmenty těla.

  • Znížení polohy těžiště těla před skokem umožňuje zvýšit délku odrazu a tím zvýšit celkovou rychlost odrazu. Skokani do délky udržují při sprintu těžiště v přibližně stejné poloze, s výjimkou posledního kroku. Při posledném kroku váznamně sníží polohu těžiště a následně vystřelí do výšky.

  • Při překonání překážky jako je skok o tyči je důležitá poloha těžiště. Proto se skokani vůči tyčce umístní tak, že jejich těžiště se nachází pod tyčkou.

Experimentální určení polohy těžiště#

Metoda balanční desky#

Pro experimentální určení polohy těžiště můžeme vyjít z definice těžiště. Postavíme-li člověka na rovnou podložku podepřenou v jednom bodě, můžeme posouvat podporu až do nalezení rovnováhy. Tento postup pak můžeme opakovat pro člověka ve stoji, v leže a v leže na boku čím získáme polohu těžište v prostoru. Tento postup jako první použil otec biomechaniky italský matematiky Giovanni Alfonso Borreli, který jako balanční podložku použil dřevenou desku.

https://d45jl3w9libvn.cloudfront.net/jaypee/static/books/9789350904947/Chapters/images/10-1.jpg

Metoda těžnic#

Umístníme-li těleso do závěsu a uvolnímě ho, vznikne kyvadlo. Po ustálení zůstane toto kyvadlo viset v rovnováze. Na těžiště můžeme nahlížet jako na bod, ve kterém je koncetrována veškerá tíhová síla. Závěs tělesa je kloub a působí v něm tedy jedna síla neznámě reakce. Na tělěso v závěsu tedy působí dvě síly: síla závěsu a síla gravitace. Proto, aby dvě síly byly v rovnováze, musí být stejně velké, opačně orientované a ležet na stejné nositelce. Protože ale víme, že gravitační síla působí vertikálně, musí pro dosažení rovnováhy platit, že těžiště se nachází na vertikální přímce procházející závěsem. Tato přímka je tak nositelkou tíhové síly působící v těžišti a označujeme jí jako těžnice.

Ze znalosti jedné těžnice nemůžeme určit polohu těžište jako bodu. Zopakujeme-li experiment ještě jednou v jiném bodě závěsu, určíme další těžnici. Poloha těžiště je polohou bodu a tak musí ležet na průsečnici těžnic.

Je-li těleso geometricky symetrické, jsou těžnice zároveň osy symetrie. Má-li těleso několik os symetrie leží těžisko v jejich přůsečníku.

Metoda silové desky#

Určování těžiště pomocí balanční desky nebo pomocí těžnic je vhodné pro tuhé tělesa. Lidské tělo se skládá ze segmentů spojených pomocí kloubů a přesnost určení těžiště uvedeným způsobem je nedostatečná. Pro určení polohy těžiště je vhodné využít metodu reakční desky, t.j. zařízení, které má ve svých podpěrách senzory pro měření síly. Pro jednoduchou představu funkčnosti dané desky nám bude stačit představa, že desku položíme na dva váhy a na desku si lehne vyšetřovaná osoba.

Tip

Určete polohu těžiště u pacienta, který má délku 180 cm a při měření na silové desce podle obrázku je podpěra A zatížena hmotností 50 kg a podpěra B zatížena hmotností 45 kg. Hmotnost desky můžeme zanedbat.

https://homework.study.com/cimages/multimages/16/figure68651149339977501176.png

Pro určení polohy těžiště budeme vycházat z rovnic rovnováhy. Danou úlohu uvolníme a budeme uvažovat, že celá tíha \(W\) působí v bodě těžiště a na desku působí reakce v uložení A (\(R_A\)) a reakce v uložení B (\(R_B\)). Je-li člověk na desce v rovnováze musí platit rovnice rovnováhy:

\[\begin{split} \begin{eqnarray} \sum\limits_i F_{ix} = 0&:& 0=0 \nonumber \\ \sum\limits_i F_{iy} = 0&:& R_A + R_B - W=0 \nonumber \\ \sum\limits_i M_{iA} = 0&:& R_B\,l + W\,x_T=0 \nonumber \end{eqnarray} \end{split}\]

Z momentové podmínky rovnováhy můžeme určit

\[x_T = \frac{R_B\,l}{W}\]

kde z silové podmínky rovnováhy do směru osi \(y\) platí

\[W = R_A + R_B \]

Pro vzdálenost těžište od podpory \(A\) (\(x_T\)) tedy platí

\[x_T = \frac{m_A\, \cancel{g}\,l}{(m_A + m_B) \cancel{g}} = \frac{ 45\,\cancel{\mathrm{kg}}\, 180\,\mathrm{cm}}{(45+55)\,\cancel{\mathrm{kg}}} = 81\,\mathrm{cm}\]

Numerické určení polohy těžiště#

Experimentální určení těžiště může být využito pro určení těžišť jednotlivých segmentů lidského těla. V průběhu pohybu dochází k rotacím v kloubech a tím pádem ke změně polohy celkového těžiště. Pro určení polohy těžiště pro libovolnou polohu těla je vhodné využít výpočet.

Z důvodu přehlednosti řěšme úlohu jako dvourozměrnou. Těžiště v prostoru se určí analogicky. Zvolíme si souřadnicový systém pro určení polohy těžiště \((x,y)\), kde os \(y\) je vertikální a střed není shodný s pozicí těžiště. Předpokládejme, že známe polohy těžišť a hmotnosti jednotlivých segmentů lidského těla. Bude-li tělo složeno z \(i=1,\dots,n\) segmentů, těžiště \(i\)-tého segmentu má souřadnice \(T_{i}[x_i, y_i]\) a hmotnost \(m_i\). Těžiště celého těla je dáno \(x_T\) a \(y_T\).

Při odvození budeme vycházet z definice těžiště, která říká, že výsledný moment tíhových sil vzhledem k těžišti je nulový. Platí tedy

\[ \sum\limits_{i=1}^{n} M_{iT} = 0\]

Moment \(i\)-tého segmentu vzhledem k celkovému těžíšti těla je roven násobku tíhové síly daného segmentu \(W_i\), která působí vertikálně a ramene \(r_i\). Rameno síly \(W_i\) je rovno \(x\)-sové vzdálenosti těžiště daného segmentu od bodu \(x_T\), t.j. \(x_i-x_T\) (osa \(y\) je rovnoběžná s nositelkou síly \(W_i\) a nezpůsobuje rotaci).

\[ M_{iT} = r_i \, W_i = (x_i - x_T)\,W_i\]

Kombinací výše uvedených vztahů dostaneme získáme

\[\begin{split} \begin{eqnarray} \label{eq:1} \sum\limits_{i=1}^{n} (x_i - x_T)\,W_i &=& 0\\ \sum\limits_{i=1}^{n} x_i\,W_i &=& \sum\limits_{i=1}^{n} x_T\,W_i\\ \sum\limits_{i=1}^{n} x_i\,W_i &=& x_T\,\sum\limits_{i=1}^{n} W_i\\ \end{eqnarray} \end{split}\]

Uvážíme-li, že tíhová síla \(W_i\) je určena hmotností \(m_i\) segmentu (\(W_i=m_i\,g\), kde \(g\) je gravitační zrychlení) můžeme napsat.

\[ x_T = \frac{\sum\limits_{i=1}^{n} x_i\,m_i}{\sum\limits_{i=1}^{n} m_i}\]

Předstame si, že tělo v rovině včetně souřadnicového systému otočíme od 90\(^\circ\). V tom případě se vymění osy \(x\) a \(y\) a nositleky tíhových sil budou rovnoběžné s osou \(x\). Výpočet těžiště vzhledem k ose \(y\) bude probíhat identicky

\[ y_T = \frac{\sum\limits_{i=1}^{n} y_i\,m_i}{\sum\limits_{i=1}^{n} m_i}\]

Note

Těžiště těla jenž se skládá z \(i=1,\dots,n\) segmentů s hmotnostmi \(m_i \) a polohou těžišť jednotlivých segmentů \((x_i,y_i)\) je možné určit pomocí vztahů

\[\begin{split} \begin{eqnarray} x_T &=& \frac{\sum\limits_{i=1}^{n} x_i\,m_i}{\sum\limits_{i=1}^{n} m_i}\\ y_T &=& \frac{\sum\limits_{i=1}^{n} y_i\,m_i}{\sum\limits_{i=1}^{n} m_i}\\ z_T &=& \frac{\sum\limits_{i=1}^{n} z_i\,m_i}{\sum\limits_{i=1}^{n} m_i} \end{eqnarray} \end{split}\]

Segmentální model těla#

Segmentální model těla je zjednodušený biomechanický model, který popisuje lidské tělo jako soustavu pevných těles (segmentů) spojených klouby. Tento model se používá k analýze pohybu, rovnováhy a dynamiky těla.

V biomechanice se tělo rozděluje na několik segmentů – například nohy, paže, trup nebo hlava – které jsou považovány za tuhá tělesa. Tento model usnadňuje výpočty pohybu, síly a momentů, které na jednotlivé části těla působí.

Segment je část těla, kterou považujeme za tuhé těleso s definovanými vlastnostmi, jako jsou:

  • Délka – vzdálenost mezi dvěma klouby nebo body spojení.

  • Hmotnost – často se uvádí jako procento z celkové tělesné hmotnosti.

  • Těžiště – bod, ve kterém je soustředěna hmotnost segmentu.

  • Moment setrvačnosti – odpor segmentu proti rotaci.

Příklady tělesných segmentů:

  • Horní končetina: paže, předloktí, ruka

  • Dolní končetina: stehno, bérec, chodidlo

  • Trup: hrudník, bederní oblast, pánev

  • Hlava

https://www.researchgate.net/publication/274723227/figure/fig4/AS:271795727106065@1441812559705/COG-center-of-each-segment-The-body-was-divided-into-seven-segments-1-Trunk-2-and.png

Kinematický řetězec?#

Kinematický řetězec je systém propojených segmentů, které jsou spojeny klouby a umožňují vzájemný pohyb. V těle je takovým řetězcem například ruka, kde je paže spojena s předloktím a rukou prostřednictvím kloubů (ramenní, loketní a zápěstní kloub).

V biomechanice se kinematické řetězce využívají k analýze pohybu a přenosu síly mezi segmenty.

Typy kinematických řetězců#

https://www.my-netti.com/app/uploads/2020/11/Kinetic-Chain-open-closed.png

Typ kinematického řetězce

Popis

Příklad v těle

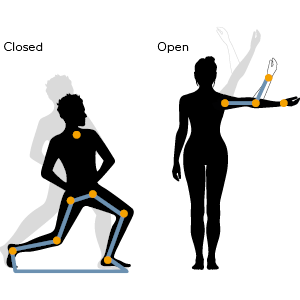
Otevřený řetězec

Pohyb začíná u pevného bodu a končí volným koncem.

Pohyb paže při zvedání činky.

Uzavřený řetězec

Oba konce řetězce jsou fixovány nebo mají kontakt s okolím.

Dřep – nohy jsou pevně na zemi.

Sériový řetězec

Segmenty jsou uspořádány lineárně za sebou.

Horní končetina (paže → předloktí → ruka).

Paralelní řetězec

Segmenty jsou uspořádány paralelně a působí současně.

Svaly, které současně stabilizují kloub.

Odhad parametrů segmentů těla#

Parametry segmentů těla (BSP) lidského těla, jako je délka, plocha, objem, hmotnost, hustota, těžiště, moment setrvačnosti a střed objemu, jsou zásadní pro aplikaci mechaniky k pochopení lidského pohybu. Antropometrie je obor zabývající se studiem takových měření lidského těla. Většinu těchto parametrů každého segmentu jedince často nelze změřit a tyto veličiny se odhadují nepřímými metodami. Hlavní nepřímé metody jsou založeny na datech mrtvol (např. Dempsterův model), skenování tělesného obrazu živých subjektů (např. Zatsiorského-Seluyanovův model) a geometrických měřeních (např. Hanavanův model).

Online dostupné přehledy různých metod používaných při odhadu BSP naleznete na Drills et al. (1964) a [Drills et al. (1964)](http://citeseerx.ist.psu.edu/viewdo52=10.2.?

Podívejme se, jak odhadnout některé z BSP pomocí antropometrického modelu Dempstera (1955) s některými parametry upravenými Winterem (2009) a modelu Zatsiorského a Selujanova (Zatsiorsky, 2002), od nynějška Zatsiorského, s parametry upravenými de Levou (1996). Existuje alespoň jedna Python knihovna pro výpočet parametrů segmentů lidského těla, viz Dembia et al. (2014), implementuje geometrický model lidské setrvačnosti Yeadon, ale zde jej nepoužijeme.

Pro tabulku s hodnotami BSP, označovanou také jako antropometrická tabulka, obvykle:

  • Hmotnost každého segmentu je uvedena jako zlomek celkové tělesné hmotnosti.

  • Poloha těžiště (CM) v sagitální rovině každého segmentu je dána jako zlomek délky segmentu vzhledem k poloze proximálního nebo distálního kloubu.

  • Poloměr otáčení (Rg) kolem příčné osy (rotace v sagitální rovině) a kolem ostatních os každého segmentu je dán jako zlomek délky segmentu vzhledem k (w.r.t.) těžišti nebo w.r.t. proximální nebo w.r.t. pozici distálního kloubu.

Formální popis těchto parametrů naleznete v poznámkovém bloku Center of Mass and Moment of Inertia.

# Importujte potřebné knihovny
import numpy as np
import pandas as pd
from IPython.display import display, Math, Latex
%matplotlib inline
import matplotlib.pyplot as plt
pd.set_option('max_colwidth', 100)

Dempsterův model upravený Wintersem#

BSP_Dmarks = pd.read_csv('https://raw.githubusercontent.com/BMClab/BMC/master/data/BSPlandmarks_Dempster.txt', sep='\t')
display(BSP_Dmarks)
Segment Definition
0 Hand Wrist axis/knuckle II middle finger
1 Forearm Elbow axis/ulnar styloid
2 Upper arm Glenohumeral axis/elbow axis
3 Forearm and hand Elbow axis/ulnar styloid
4 Total arm Glenohumeral joint/ulnar styloid
5 Foot Lateral malleolus/head metatarsalII
6 Leg Femoral condyles/medial malleolus
7 Thigh Greater trochanter/femoral condyles
8 Foot and leg Femoral condyles/medial malleolus
9 Total leg Greater trochanter/medial malleolus
10 Head and neck C7-T1 and 1st rib/ear canal
11 Shoulder mass Sternoclavicular joint/glenohumeral
12 Thorax C7-T1/T12-L1 and diaphragm
13 Abdomen T12-L1/L4-L5
14 Pelvis L4-L5/greater trochanter
15 Thorax and abdomen C7-T1/L4-L5
16 Abdomen and pelvis T12-L1/greater trochanter
17 Trunk Greater trochanter/glenohumeral joint
18 Trunk head neck Greater trochanter/glenohumeral joint
19 Head, arms, and trunk (HAT) Greater trochanter/glenohumeral joint
20 HAT Greater trochanter/mid rib 
BSP_Dmarks = pd.read_csv('https://raw.githubusercontent.com/BMClab/BMC/master/data/BSP_DempsterWinter.txt', sep='\t')
display(BSP_Dmarks)
Segment Definition Mass CM prox CM dist Rg CM Rg prox Rg dist
0 Hand WJC-KNU2 0.0060 0.506 0.494 0.297 0.587 0.577
1 Forearm EJC-STYL 0.0160 0.430 0.570 0.303 0.526 0.647
2 Upper arm SJC-EJC 0.0280 0.436 0.564 0.322 0.542 0.645
3 Forearm hand EJC-STYL 0.0220 0.682 0.318 0.468 0.827 0.565
4 Total arm SJC-STYL 0.0500 0.530 0.470 0.368 0.645 0.596
5 Foot LMAL-MT2 0.0145 0.500 0.500 0.475 0.690 0.690
6 Leg KJC-MMAL 0.0465 0.433 0.567 0.302 0.528 0.643
7 Thigh GTR-KJC 0.1000 0.433 0.567 0.323 0.540 0.653
8 Head neck C7T1-RIB1EAR 0.0810 1.000 0.000 0.495 0.116 NaN
9 Thorax C7T1-T12L1-DIAP 0.2160 0.820 0.180 NaN NaN NaN
10 Abdomen T12L1-GTR 0.1390 0.440 0.560 NaN NaN NaN
11 Pelvis L4L5-GTR 0.1420 0.105 0.895 NaN NaN NaN
12 Trunk GTR-SJC 0.4970 0.500 0.500 NaN NaN NaN
13 Trunk head neck GTR-SJC 0.5780 0.660 0.340 0.503 0.830 0.607
14 HAT GTR-SJC 0.6780 0.626 0.374 0.496 0.798 0.621
15 Foot leg KJC-MMAL 0.0610 0.606 0.394 0.416 0.735 0.572
16 Total leg GTR-MMAL 0.1610 0.447 0.553 0.326 0.560 0.650
17 Thorax abdomen C7T1-L4L5 0.3550 0.630 0.370 NaN NaN NaN
18 Abdomen pelvis T12L1-GTR 0.2810 0.270 0.730 NaN NaN NaN

Zatsiorského model upravený de Levou#

Segmenty definované v Zatsiorského modelu (Zatsiorsky, 2002) upravené de Levou (1996) jsou znázorněny na následujícím obrázku.

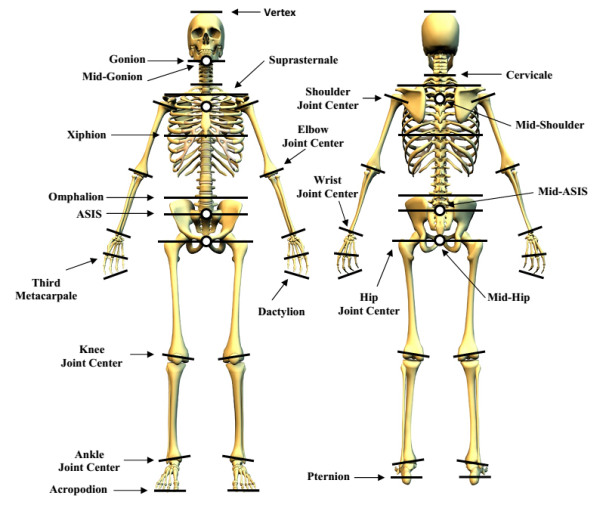
Zatsiorského antropometrický model
Obrázek. Definice segmentu použitá v antropometrickém modelu Zatsiorského a Selujanova (Zatsiorsky, 2002) upravená de Levou (1996).
Obrázek z manuálu Motion Analysis Corporation.
BSP_Zmarks = pd.read_csv('https://raw.githubusercontent.com/BMClab/BMC/master/data/BSPlandmarks_ZdeLeva.txt', sep='\t')
display(BSP_Zmarks)
Landmark Name Abbreviation Description
0 Acromion ACRO Most lateral point on the lateral edge of the acromial process of the scapula
1 Acropodion TTIP Tip of longest toe
2 Bispinous breadth BB Distance between two ASIS
3 Cervicale CERV Superior tip of the spine of the 7th certical vertebra
4 Dactylion (3rd) DAC3 Tip of 3 rd digit
5 Gonion GONI Most lateral point on the posterior angle of mandible
6 Iliospinale ASIS Inferior point of one of the anterior superior iliac spines
7 Malleoli MMAL, LMAL Medial and lateral bony projections of the malleolus
8 Metacarpale (3rd) MET3 Distal palpable point on the metacarpal of the 3rd digit on the dorsal hand
9 Mid-gonion MIDG Point midway between 2 gonion
10 Mid-hip MIDH Point midway between 2 hip joint centers
11 Mid-shoulder MIDS Point midway between 2 shoulder joint centers
12 Omphalion OMPH Center of navel
13 Pternion HEEL Posterior point of the heel
14 Radiale RADI Lateral tip on the proximal head of the radius
15 Sphyrion (tibia) TSPH Distal tip of the tibia – distal to medial malleolus
16 Sphyrion fibulare FSPH Distal tip of the fibula – distal to lateral malleolus
17 Stylion RSTY Distal dip of the styloid process of the radius
18 Suprasternale SUPR Most caudal point on the jugular notch on the sternum
19 Tibiale (medial) MTIB Most proximal point on the medial superior border of the head of the tibia
20 Tibiale laterale LTIB Most proximal point on the lateral superior border of the head of the fibula
21 Trochanterion TROC Superior border on the greater trochanter of the femur
22 Vertex VERT Uppermost part of the head
23 Xiphion XYPH Lowermost end of the sternum 
bsp_Zf = pd.read_csv('https://raw.githubusercontent.com/BMClab/BMC/master/data//BSPfemale_ZdeLeva.txt', index_col=0, sep='\t')
display(Latex('Parametry těla - žena, from Zatsiorsky\'s model upravený de Leva (1996):'))
display(bsp_Zf)
\[Parametry těla - žena, from Zatsiorsky's model upravený de Leva (1996):\]
Endpoints Mass CM Long Rg Sag Rg Trans Rg Long
Segment
Head VERT-MIDG 0.0668 0.5894 0.330 0.359 0.318
Trunk SUPR-MIDH 0.4257 0.4151 0.357 0.339 0.171
Upper trunk SUPR-XYPH 0.1545 0.2077 0.746 0.502 0.718
Middle trunk XYPH-OMPH 0.1465 0.4512 0.433 0.354 0.415
Lower trunk OMPH-MIDH 0.1247 0.4920 0.433 0.402 0.444
Upper arm SJC-EJC 0.0255 0.5754 0.278 0.260 0.148
Forearm EJC-WJC 0.0138 0.4559 0.261 0.257 0.094
Hand WJC-MET3 0.0056 0.7474 0.531 0.454 0.335
Thigh HJC-KJC 0.1478 0.3612 0.369 0.364 0.162
Shank KJC-AJC 0.0481 0.4352 0.267 0.263 0.092
Foot HEEL-TTIP 0.0129 0.4014 0.299 0.279 0.139
Head 2 VERT-CERV 0.0668 0.4841 0.271 0.295 0.261
Trunk 2 CERV-MIDH 0.4257 0.4964 0.307 0.292 0.147
Trunk 3 MIDS-MIDH 0.4257 0.3782 0.379 0.361 0.182
Upper trunk 2 CERV-XYPH 0.1545 0.5050 0.466 0.314 0.449
Forearm 2 EJC-STYL 0.0138 0.4592 0.263 0.259 0.095
Hand 2 WJC-DAC3 0.0056 0.3427 0.244 0.208 0.154
Hand 3 STYL-DAC3 0.0056 0.3502 0.241 0.206 0.152
Hand 4 STYL-MET3 0.0056 0.7534 0.519 0.443 0.327
Shank 2 KJC-LMAL 0.0481 0.4416 0.271 0.267 0.093
Shank 3 KJC-SPHY 0.0481 0.4481 0.275 0.271 0.094 
bsp_Zm = pd.read_csv('https://raw.githubusercontent.com/BMClab/BMC/master/data/BSPmale_ZdeLeva.txt', index_col=0, sep='\t')
display(Latex('Parametry těla - muž, from Zatsiorsky\'s model upravený de Leva (1996):'))
display(bsp_Zm)
\[Parametry těla - muž, from Zatsiorsky's model upravený de Leva (1996):\]
Endpoints Mass CM Long Rg Sag Rg Trans Rg Long
Segment
Head VERT-MIDG 0.0694 0.5976 0.362 0.376 0.312
Trunk SUPR-MIDH 0.4346 0.4486 0.372 0.347 0.191
Upper trunk SUPR-XYPH 0.1596 0.2999 0.716 0.454 0.659
Middle trunk XYPH-OMPH 0.1633 0.4502 0.482 0.383 0.468
Lower trunk OMPH-MIDH 0.1117 0.6115 0.615 0.551 0.587
Upper arm SJC-EJC 0.0271 0.5772 0.285 0.269 0.158
Forearm EJC-WJC 0.0162 0.4574 0.276 0.265 0.121
Hand WJC-MET3 0.0061 0.7900 0.628 0.513 0.401
Thigh HJC-KJC 0.1416 0.4095 0.329 0.329 0.149
Shank KJC-AJC 0.0433 0.4395 0.251 0.246 0.102
Foot HEEL-TTIP 0.0137 0.4415 0.257 0.245 0.124
Head 2 VERT-CERV 0.0694 0.5002 0.303 0.315 0.261
Trunk 2 CERV-MIDH 0.4346 0.5138 0.328 0.306 0.169
Trunk 3 MIDS-MIDH 0.4346 0.4310 0.384 0.358 0.197
Upper trunk 2 CERV-XYPH 0.1596 0.5066 0.505 0.320 0.465
Forearm 2 EJC-STYL 0.0162 0.4608 0.278 0.267 0.122
Hand 2 WJC-DAC3 0.0061 0.3624 0.288 0.235 0.184
Hand 3 STYL-DAC3 0.0061 0.3691 0.285 0.233 0.182
Hand 4 STYL-MET3 0.0061 0.7948 0.614 0.502 0.392
Shank 2 KJC-LMAL 0.0433 0.4459 0.255 0.249 0.103
Shank 3 KJC-SPHY 0.0433 0.4524 0.258 0.253 0.105

Rozdíly mezi antropometrickými modely od Dempstera a Zatsiorského#

Antropometrické modely od Dempstera a Zatsiorského se v mnoha aspektech liší; pokud jde o předměty zkoumané ve studiích, Dempsterův model je založen na datech 8 mrtvol starších mužů (ale dva z nich byli neznámého věku) analyzovaných ve Spojených státech. Zatsiorského model je založen na skenování obrazu 100 mladých mužů a 15 mladých žen, v té době všichni studenti vojenské školy v bývalém Sovětském svazu.

Rozdíl mezi modely pro některé segmenty je velký (viz tabulka níže): hmotnostní podíl stehenního segmentu u modelu Zatsiorského je o více než 40 % větší než u modelu Dempster, naopak, segment trupu má u modelu Zatisorského asi o 15 % nižší hmotnostní podíl. Všimněte si také, že některé segmenty nemají v obou modelech stejnou definici.

m_D = bsp_D.loc[['Foot', 'Leg', 'Thigh', 'Pelvis', 'Abdomen', 'Thorax', 'Trunk',
                   'Upper arm', 'Forearm', 'Hand', 'Head neck'], 'Mass']
m_Zf = bsp_Zf.loc[['Foot', 'Shank', 'Thigh', 'Lower trunk', 'Middle trunk', 'Upper trunk',
                   'Trunk', 'Upper arm', 'Forearm', 'Hand', 'Head'], 'Mass']
m_Zm = bsp_Zm.loc[['Foot', 'Shank', 'Thigh', 'Lower trunk', 'Middle trunk', 'Upper trunk',
                   'Trunk', 'Upper arm', 'Forearm', 'Hand', 'Head'], 'Mass']
m_D.index = m_Zf.index  # kvůli různým názvům některých segmentů

display(Latex("Relativní rozdíl hmotností (v %) modelu Zatsiorského vůči modelu podle Dempstera"))
d = pd.DataFrame({'Females': np.around(100 * (m_Zf - m_D) / m_D), \
                  'Males': np.around(100 * (m_Zm - m_D) / m_D)})
display(d)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/tmp/ipykernel_85167/1518022555.py in <module>
----> 1 m_D = bsp_D.loc[['Foot', 'Leg', 'Thigh', 'Pelvis', 'Abdomen', 'Thorax', 'Trunk',
      2                    'Upper arm', 'Forearm', 'Hand', 'Head neck'], 'Mass']
      3 m_Zf = bsp_Zf.loc[['Foot', 'Shank', 'Thigh', 'Lower trunk', 'Middle trunk', 'Upper trunk',
      4                    'Trunk', 'Upper arm', 'Forearm', 'Hand', 'Head'], 'Mass']
      5 m_Zm = bsp_Zm.loc[['Foot', 'Shank', 'Thigh', 'Lower trunk', 'Middle trunk', 'Upper trunk',

NameError: name 'bsp_D' is not defined

Změna těžiště v průběhu růstu#

Poloha těžiště lidského těla se mění v průběhu růstu od dětství až do dospělosti. Tato změna je dána především změnami proporcí těla a rozložením hmotnosti.

Novorozenci a kojenci#

  • Těžiště je poměrně vysoko, v oblasti hrudníku.

  • Hlava tvoří velkou část celkové hmotnosti.

  • Nestabilita, potřeba opory.

Dětství#

  • Těžiště se posouvá níže, k pánvi.

  • Dolní končetiny a trup se vyvíjejí rychleji než hlava.

  • Zlepšení stability a rovnováhy.

Dospívání#

  • Další změny v proporcích těla.

  • U dívek se těžiště posouvá o něco níže než u chlapců (rozdíly v rozložení svalové hmoty a tukové tkáně).

  • U dospělých se těžiště nachází v oblasti bederní páteře.

Dospělost#

  • Těžiště se ustálí.

  • Poloha těžiště se může měnit s ohledem na pohlaví a změny hmotnosti.

Klíčové faktory ovlivňující změnu těžiště#

  • Proporce těla (relativní velikost hlavy, trupu a končetin).

  • Rozložení hmotnosti (svalová hmota a tuková tkáň).

  • Pohlaví.

COG, COM, LOG, COP#

  • 1. COG (Center of Gravity) – Těžiště

    • Definice: Bod, ve kterém je soustředěna celková váha tělesa a kde působí gravitační síla.

    • V biomechanice: U člověka se těžiště obvykle nachází kolem druhého sakrálního obratle (S2), ale jeho poloha se mění v závislosti na držení těla a pohybu (např. při zvedání rukou se těžiště posouvá nahoru).

    • Praktický význam: Stabilita těla závisí na poloze těžiště vzhledem k opěrné ploše. Pokud těžiště zůstává nad opěrnou plochou, člověk zůstává stabilní.

    https://pdhpe.net/wp-content/uploads/2017/05/Line-of-Gravity-photo.png

  • 3. LOG (Line of Gravity) – Těžnice

    • Definice: Svislá čára, která prochází skrz COG (nebo COM) směrem k zemi, v souladu s gravitační silou.

    • V biomechanice: U stojící osoby by měla tíhová čára procházet blízko uprostřed základny opory (např. mezi chodidly).

    • Praktický význam: Stabilita závisí na tom, zda tíhová čára zůstává uvnitř základny opory. Pokud se dostane mimo tuto základnu (např. při předklonu), tělo ztrácí stabilitu a musí zapojit svaly k udržení rovnováhy.

  • 2. COM (Center of Mass) – Těžiště hmotnosti

    • Definice: Bod, kde je rovnoměrně rozložena celková hmota tělesa ve všech směrech. Z pohledu člověka jsou COM a COG na stejném místě.

      Warning

      V biomechanice se někdy pojmem COG označuje průmět COM na podložku.

    https://www.researchgate.net/publication/371564125/figure/fig1/AS:11431281186182084@1693825407421/A-P-human-balance-in-standing-posture-A-P-anteroposterior_W640.jpg https://www.researchgate.net/publication/371564125/figure/fig2/AS:11431281186182086@1693825407622/COP-and-COG-trajectories-during-locomotion-COG-centre-of-gravity-COP-centre-of_W640.jpg

  • 4. COP (Center of Pressure) – Těžiště tlaku

    • Definice: Bod na povrchu podložky, kde je výslednice tlakových sil působících na tělo.

    • V biomechanice: COP je dynamický bod, který se neustále mění v závislosti na pohybu a rovnovážné reakci těla. Nejčastěji se měří pomocí silové desky při analýze rovnováhy a stability.

    • Praktický význam: Sleduje se při diagnostice poruch rovnováhy a analýze chůze. Při stojícím postoji ukazuje, jak tělo aktivně upravuje svalovou aktivitu k udržení rovnováhy. Pokud je COP mimo základnu opory, hrozí pád.

      Warning

      Trajektorie COP je je zcela nezávislá na poloze COM a je to poloha vektoru reakční síly ze silové plošiny. Tyto síly závisí na umístění chodidla a motorickém řízení svalů. COP je tedy neuromuskulární odezva na nevyváženost tělesné rovnováhy.

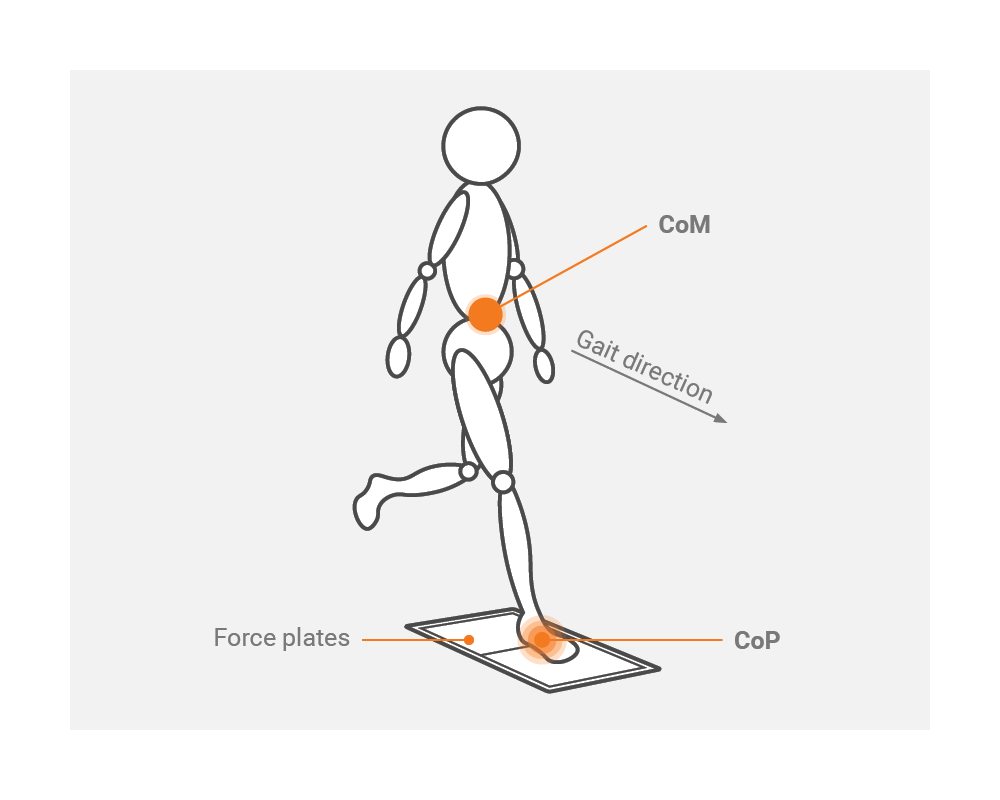
https://images.ctfassets.net/98s79sqwuajy/3S7UVzwCshyNd0szADDwkh/7491b54b7ccfa0f3eb1bf015a0eaa947/211201_RS_CoP-CoM_BlogFigure_RGB.webp

Těžiště (COG) při různých aktivitách#

Poloha těžiště se liší u každého jedince, zejména u sportovců. Sportovec s delšími a/nebo většími nohami bude mít pravděpodobně nižší těžiště, pokud jeho horní část těla není také relativně velká a nevyrovnává hmotnost dolní části těla.

U běžců se těžiště nachází v dolní (inferiorní) oblasti pánve a před (anteriorně) tělem, protože běžec se obvykle naklání dopředu, což pomáhá při akceleraci.

Snížení polohy těžiště pomáhá zvýšit rovnováhu a stabilitu, protože je nutné jej zvednout výše, než se přesune mimo opěrnou plochu (BOS - Base of Support). To lze vidět u některých jógových a balančních pozic, gymnastiky, atletických disciplín a dokonce i při stojce na rukou.

Při nošení předmětů, jako je kufr, nákupní taška nebo batoh, se těžiště mění, protože se hmotnost přidává do příslušných oblastí těla. Toto těžiště se mění s hmotností a polohou neseného předmětu a také s polohou a pohybem těla.

from IPython.display import YouTubeVideo

YouTubeVideo('5s1gEi5wfLg', width=600, height=300)