Práce a energie

Přenos energie pomocí práce

Co se stane s energií při vykonání práce?

Když je na systém vykonána práce, energie je do něj přenesena. Energie může v systému zůstat uložena nebo být přenesena dál.

• Například pokud tlačíme sekačku jen tak, aby se pohybovala stálou rychlostí, pak je energie dodaná člověkem neustále odváděna třením a nakonec opouští systém ve formě tepla.

• Naproti tomu při nosení aktovky do schodů se práce ukládá jako potenciální energie v systému „aktovka-Země“. Tato energie může být kdykoliv znovu využita.

• Stavební techniky ve starověkém Egyptě (např. stavba pyramid) jsou historickým příkladem ukládání energie do systému pomocí vykonané práce.

Práce a energie

Ze Newtonových zákonů víme, že síla způsobuje zrychlení. Práce \(W_{\text{net}}\) je definována jako součet všech prací vykonaných vnějšími silami – tedy jako práce vykonaná výslednou silou \(F\):

\[ W = F \cdot d \cdot \cos \theta \]

kde:

• \(d\) je posunutí,

• \(\theta\) je úhel mezi vektorem síly a vektorem posunutí.

Grafická interpretace

• Pokud je \(F \cdot \cos\theta\) konstantní, pak plocha pod grafem síly vůči dráze představuje vykonanou práci:

  \[ W = F \cdot d \cos\theta \]

• Pokud se síla mění, rozdělíme oblast pod křivkou na úseky. Práce v každém úseku je:

\[ W_i = (F \cos\theta)^{\text{ave}}_i d_i \]

Celková práce je tedy součtem ploch pod křivkou, tj. celkovou energií přenesenou do systému.

---

Práce a kinetická energie

Z druhého Newtonova zákona plyne:

\[ F = m a \]

Dosazením do vztahu pro práci:

\[ W = m a d \]

Použijeme známou rovnost pro pohyb s konstantním zrychlením:

\[ v = v_0 + a t \]

\[ v^2 = v_0^2 + 2 v_0 a t + a^2 t^2 \]

a

\[ d = v_0 t + \frac{1}{2} a t^2 \]

\[ 2 a d = 2 v_0 a t + a^2 t^2 \]

\[ v^2 = v_0^2 + 2 a d \]

Vyjádříme z ní zrychlení:

\[ a = \frac{v^2 - v_0^2}{2d} \]

Dosadíme zpět:

\[ W = m \left( \frac{v^2 - v_0^2}{2d} \right) d \]

Zkrátíme \(d\) a dostáváme:

\[ W = \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2 \]

Práce je rovna změně kinetické energie

\[ W = \Delta E_k = \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2 \]

Práce vykonaná na tělese vede ke změně jeho pohybové energie. Platí obecně, i pokud se síly mění nebo nejsou ve směru pohybu.

Práce a potenciální energie

Chůze do schodů nebo zvedání předmětů je práce – jak ve vědeckém, tak i v běžném smyslu slova. Jedná se o práci vykonanou proti gravitační síle.

Když se vykonává práce, dochází ke změně energie – konkrétně ke vzniku uložené (potenciální) energie. V této části se zaměříme právě na gravitační potenciální energii.

Představme si těleso o hmotnosti \(m\), které zvedneme o výšku \(h\). Pokud ho zvedáme rovnoměrně (bez zrychlení), síla potřebná ke zvednutí je rovna jeho tíze \(mg\).

Práce vykonaná na tělese je pak:

\[ W = F d = mg h \]

Tuto práci definujeme jako gravitační potenciální energii \(E_p\), která byla předána (nebo získána) systému těleso-Země.

Co je gravitační potenciální energie?

Tato energie je spojena se stavem vzájemného oddělení dvou objektů, které se navzájem přitahují gravitační silou – tedy například Země a zvedaného předmětu.

• Pro zjednodušení mluvíme o „energie získané tělesem“, ale ve skutečnosti jde o energii uloženou v gravitačním poli Země.

• Používáme slovo „systém“, protože potenciální energie není vlastností samotného objektu, ale celého systému – tedy těleso + Země.

• Tato energie závisí na poloze tělesa vůči okolí, nikoliv pouze na něm samotném.

Síla, kterou na těleso působíme (např. rukou), je vnější síla – pochází mimo systém těleso-Země. Tato síla vykonává kladnou práci a tím zvyšuje potenciální energii systému.

Referenční hladina

Protože gravitační potenciální energie závisí na relativní poloze, potřebujeme si zvolit referenční bod, kde bude energie rovna nule.

• Nejčastěji volíme povrch Země jako hladinu, kde \(E_p = 0\).

• Tento výběr je libovolný – důležité je, že ve fyzice záleží jen na rozdílu potenciálních energií mezi dvěma body, protože práce závisí právě na tomto rozdílu.

Například rozdíl potenciální energie mezi dvěma příčkami žebříku je stejný, ať už se jedná o spodní nebo horní část žebříku.

Potenciální energie pružiny

Pružina vykonává sílu podle Hookeova zákona:

\[ F = -kx \]

kde:

• \(F\) je síla vyvolaná deformací pružiny,

• \(k\) je tuhost (pružinová konstanta),

• \(x\) je prodloužení (nebo stlačení) pružiny vzhledem k rovnovážné poloze.

Chceme spočítat práci vykonanou při natažení pružiny z rovnovážné polohy \(x = 0\) do nové polohy \(x\), což odpovídá energii uložené v pružině – tzv. deformační energii.

Síla při natahování pružiny není konstantní, ale roste lineárně od 0 do ( kx ). Na grafu závislosti síly \(F_\) na deformaci \(x\) (lineární růst), je práce vykonaná silou rovna ploše pod křivkou:

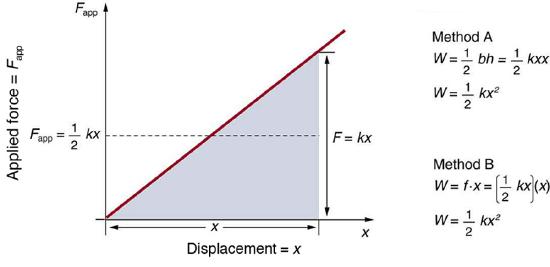
• Metoda A: Plocha pod grafem síly je:

  \[ W = \frac{1}{2} k x^2 \]

• Metoda B:

  Síla roste lineárně od 0 do \(kx\) takže průměrná síla je:

  \[ F_{\text{prům}} = \frac{1}{2} kx \]

  Práce je pak síla krát dráha:

  \[ W = F_{\text{prům}} x = \left( \frac{1}{2} kx \right) x = \frac{1}{2} k x^2 \]

Tato energie je uložena v pružině v důsledku její deformace, a může být opět uvolněna při návratu do rovnovážné polohy.

Caution

Záporné znaménko v Hookeově zákonu značí, že síla pružiny je proti směru deformace, ale pro výpočet energie bereme kladnou práci vykonanou proti síle pružiny.