Chůze a zákony zachování

Změna kinetické energie

Na rozdíl od létání a plavání, kde tělo může klouzat vůči okolnímu médiu, pohyb na nohou na zemi je omezen pevným bodem kontaktu, který noha vytváří se zemí při každém kroku (Tucker, 1973). Během chůze dochází k několika důležitým energetickým procesům, které ovlivňují pohyb a stabilitu těla.

Když je během kroku bod kontaktu před těžištěm těla, tělo zpomaluje dopředu, díky spojení mezi těžištěm a bodem kontaktu. To vede k ztrátě kinetické energie pohybu vpřed.

\[ \Delta E_k = \frac{1}{2} m (v_{f, \text{max}}^2 - v_{f, \text{min}}^2) \]

kde:

• \(m\) je hmotnost těla

• \(v_{f, \text{max}}\) a \(v_{f, \text{min}}\) jsou maximální a minimální hodnoty rychlosti těžiště při každém kroku.

Aby byla udržena konstantní průměrná rychlost kroku, musí být ztráta kinetické energie, ke které dochází při každém kroku, obnovena opětovným zrychlením těla vpřed, což vyžaduje práci a výdej energie.

Obnova energie při zvedání těla

Naštěstí, stejně jako při skoku o tyči, energie pro spomalení vykonaná během dopadu jedné nohy proti druhé je uložena zvednutím těla \(h\) jako zvýšení gravitační potenciální energie.

\[ \Delta E_p = m g h \]

kde:

• \(m\) je hmotnost těla

• \(g\) je gravitační zrychlení

• \(h\) je zvednutí těla.

Změna potenciální na kinetickou energii

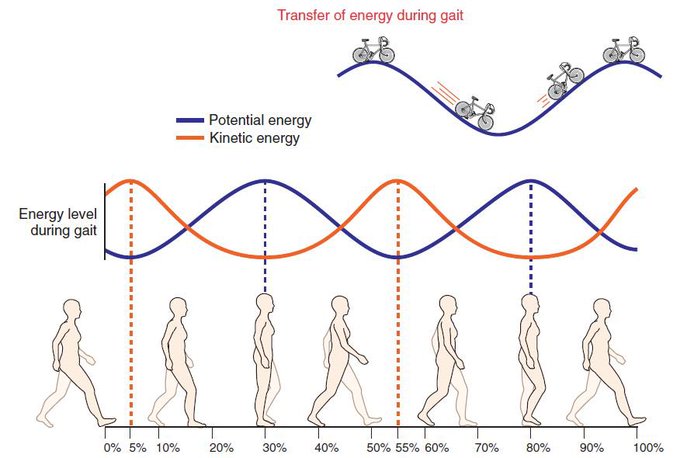
Po zvednutí tělo “padá vpřed”, čímž obnovuje kinetickou energii \(E_{k}\) na úkor potenciální energie \(E_p \). Tímto způsobem je část mechanické energie uchována pomocí mechanismu kyvadla.

Rozdíl mezi chůzí a kyvadlem

Na rozdíl od kyvadla však dvě změny energie při chůzi nejsou přesnými zrcadlovými obrazy sebe navzájem, což má za následek, že pro udržení pohybu těžiště v sagitální rovině je nutné vykonat práci svaly.

Účinnost mechanismu kyvadla

Účinnost mechanismu kyvadla během chůze byla hodnocena měřením podílu celkových změn mechanické energie těžiště, který je obnoven v důsledku proměny mezi \(E_p\) a \(E_{k}\).

\[ \text{Recovery} = \frac{W_v + W_f - W_\text{ext}}{W_v + W_{f}} = 1- \frac{W_\text{ext}}{W_v + W_{f}} \]

kde:

• \(W_v\) představuje amplitudu křivky \(E_p\), tj. pozitivní práci (\(W_v = \Delta E_p\)) vykonanou při každém kroku pro zvednutí těžiště

• \(W_f = \Delta E_{k}\) představuje amplitudu křivky kinetické energie \(E_{k}\)

• \(W_{\text{ext}}\) je celková pozitivní vnější práce, která je skutečně vykonána při každém kroku pro udržení pohybu těžiště v sagitální rovině.

Aby byl optimalizován proces obnovy mechanické energie, musí mít křivky kinetické a gravitační potenciální energie stejný tvar, mít stejnou amplitudu a být v opačné fázi, jako u kyvadla.