Biomechanika skoku z místa

import numpy as np
from IPython.display import IFrame

Fáze skoku z místa

Nejjednodušším pohybem k analýze je skok z místa. Předpokládáme, že těžiště skokana se pohybuje po přímce směrem nahoru a dolu. protože to představuje jednoduchý přímočarý pohyb. Skok do výšky můžeme rozdělit do několika částí:

1. Podřep: Před skokem je nutno se přikrčit, protože pak můžeme při narovnání působit na podložku sílou.

2. Odrazová fáze: Začíná z podřepu, kdy skokan tlačí nohama proti zemi, dokud se chodidla neodlepí od povrchu.

3. Letová fáze: Od okamžiku, kdy se chodidla odlepí od země, až do dosažení maximální výšky těžiště.

4. Pádová fáze: Od dosažení maximální výšky až po dotyk ze zemí.

5. Dopadová fáze: Od dotyku se zemí po dosažení stabilní polohy těžiště.

Analýza skoku

Pro zjednodušení analýzy se soustředíme se pouze na pohyb těžiště. Jinými slovy předpokládáme, že během skoku se poloha těla a držení těla nemění. Pro odraz je nutno získat určitý impulz síly.

Během odrazové fáze působí na nohy síla \(R(t)\), kterou vyvolává odpovídající reakční síla země. Použitím druhého Newtonova zákona získáme:

\[ F(t) = m a(t) \]

kde \(F(t)\) je výsledná síla působící v čase \(t\). Pomocí impulzu síly můžeme vyjádřit

\[ I = \sum\limits_i F_i(t) \Delta t_i = m v \]

kde v jednotlivých časových úsecích \(\Delta t_i\) působí na tělo výslední síla \(F_i\). Na tělo působí síla gravitace \(W\) a síla od podložky \(R(t)\)

\[ \sum\limits_i (R_i(t)- W) \Delta t_i = m v \]

kde \(R_i(t)\) je síla v daném časovém okamžiku.

Průměrná reakční síla

Síla \(R\) se mění v čase a proto musíme sečíst jednotlivé impulzy působící síly. Abychom mohli pokračovat v analýze, musíme znát časový průběh síly \(R(t)\). Experimentální data ukazují, že během podřepu je reakční síla menší než tělesná hmotnost, ale při odrazu se zvětšuje nad tělesnou hmotnost, což odpovídá pozitivní akceleraci směrem nahoru.

Pro zjednodušení nahradíme skutečný průběh síly ekvivalentní konstantní silou \(F_{\text{equiv}}\). Ekvivalentní síla je sílou, která ma stejný účinek (impulz síly) jako síla, která probíha. Jinými slovy plocha pod křivkou síly \(F(t)\) je stejna jako velikost obdélníku \(F_\mathrm{equiv}t\). Její význam je stejný jako význam průměrné síly.

Můžeme tedy napsat: $\( (F_\mathrm{equiv} - W) t = m v \)$

Odrazová rychlost

Působí je na tělo konstatní síla, pohybuje se rovnoěmrně zrychleně. Předpokládejme, že před odrazem se těžiště sníží o hodnotu \(c\). Tato délka je zároveň dráhou rovnoměrně zrychleného pohybu. pro který platí

\[c = \frac{1}{2} v t \]

a čas nutný k odrazu je

\[t = \frac{2 c}{v} \]

Pro odrazovou rychlost tedy můžeme odvodit

\[ (F_\mathrm{equiv} - W) \frac{2 c}{v} = m v \]

\[ v = \sqrt{\frac{2 c}{m}(F_\mathrm{equiv} - W)} \]

Výška dosažená během letu

Ve vzdušné fázi je tělo skokana vystaveno pouze gravitaci \(g\), a tedy pohyb je rovnoměrně spomalený- Výška dosažená těžištěm \(h\) je určena podmínkou dosažení maximálního bodu kdy je rychlost nulová

\[ v - g t = 0 \]

\[ t = \frac{v}{g} \]

Caution

Všimněte si, že doba letu po maximální bod a doba následného volného pádu \(v=gt\) pádu jsou stejné. Zároveň platí, že odrazová vertikální rychlost je stejná jako dopadová rychlost.

A pro dráhu rovnoměrně spomaleného pohybu můžeme napsat

\[ h = v t - \frac{1}{g}t^2 \]

\[ h = v \frac{v}{g} - \frac{1}{2}{g}\frac{v^2}{g^2} \]

\[ h = \frac{1}{2}{g}{v} \]

Ze znalosti odrazové rychlosti můžeme napsat

\[h = c \frac{F_\mathrm{equiv} - W}{m g} \]

nebo s uvážením, že \(W = m g\)

\[h = c \left(\frac{F_\mathrm{equiv}}{W}-1\right) \]

což ukazuje, že výška skoku závisí na hloubce podřepu \(c\) a průměrné odrazové síle \(F_\text{equiv}\).

Za předpokladu, že \(F_\mathrm{equiv} = 2 W\) vyskočímě přibližně do výšky původního podřepu \(h=c\).

Skok z dřepu a skok s protipohybem

Časový průběh vertikální reakční síly (osa y) při skoku s protipohybem (CMJ) a skoku z dřepu (SJ). Ačkoli CMJ vede k vyššímu skoku, vyžaduje také více času na provedení (osa x). Podle Van Hooren, B., & Bosch, F. (2016). Influence of muscle slack on high-intensity sport performance: A review. Strength & Conditioning Journal, 38(5), 75–87. https://doi.org/10.1519/SSC.0000000000000251

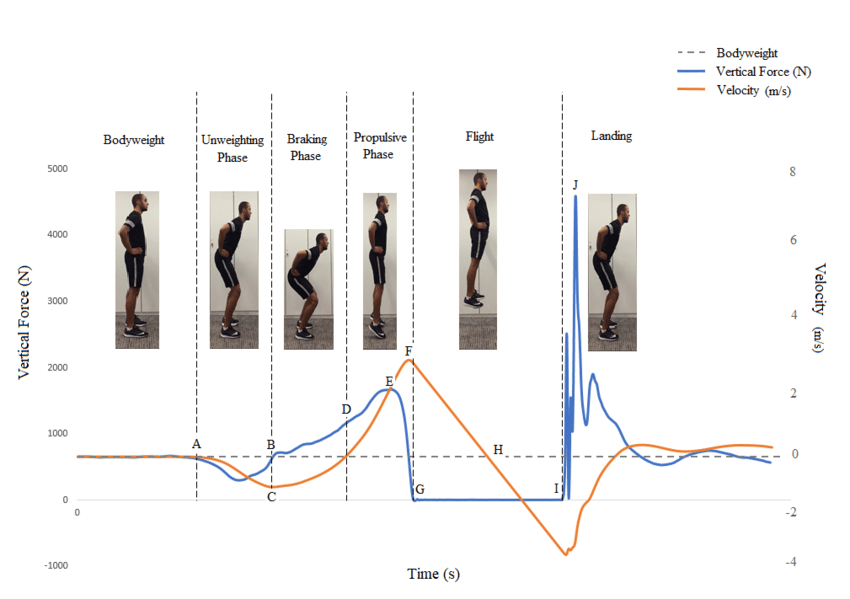
Skok s protipohybem countermovement jump (CMJ) je vertikální skok, který zahrnuje předchozí pohyb opačným směrem – tedy proti směru následného odrazu. Tento typ skoku je běžně používán k hodnocení vertikální výbušnosti sportovců.

V nejjednodušší podobě lze protipohyb chápat jako pohyb dolů následovaný opačným pohybem nahoru. V případě CMJ se jedná o prodloužení určitých svalů při poklesu těžiště před odrazem, kde tyto svaly brzdí pohyb a působí excentrickou kontrakcí. Jakmile sportovec dosáhne nejnižší polohy (dosednutí do podřepu), krátce se zastaví (izometrická nebo amortizační fáze), než zahájí koncentrickou svalovou činnost (propulzní fázi), která vyústí ve vertikální skok.

Podřep tak můžeme rozdělit do dvou fází:

1. Fáze odlehčení - kdy stoupá rychlost směrem k podložce

2. Fáze brždění - kdy zapojením svalů sportovec překonává inerciální sílu (setrvačnost těla) a tím se postupně zastavuje

Note

Výzkumy ukazují, že CMJ obvykle umožňuje dosáhnout vyššího výskoku než squat jump (SJ), a to přibližně o 20–30 %. Tento rozdíl je dán schopností využít elastickou energii uloženou ve svalech a šlachách během poklesu těžiště, kdy svaly mohou působit větší než izometrickou sílou.

Výška skoku je odhad změny výšky těžiště sportovce a nejpřesněji ji lze určit pomocí dat ze silové plošiny. Kromě samotné výšky skoku lze měřit i další parametry, avšak jejich získání vyžaduje specializované vybavení, jako je právě silová plošina. Z tohoto důvodu se tyto veličiny běžně neměří ve většině tréninkových prostředí. Přesto poskytují podrobnější obraz o fyzickém profilu sportovce. Mezi klíčové proměnné patří:

• Maximální síla (N)

• Relativní maximální síla (N·kg⁻¹)

• Maximální výkon (W)

• Maximální rychlost (m·s⁻¹)

• Rychlost vývoje síly (N·s⁻¹)

• Impuls síly (N·s)

Nejvyšší skok Christiana Ronalda

IFrame("https://www.olympics.com/en/news/cristiano-ronaldo-highest-jumps-football-vertical-leap", 900,500)

V historii fotbalu je nejvyšší zaznamenaný výskok Cristiana Ronalda. V únoru 2013 předvedl Ronaldo při zápase Realu Madrid proti Manchesteru United v osmifinále Ligy mistrů UEFA výskok do výšky 2,93 metru. Když vememe, že výška Ronalda je 1.87 m, výška výskoku byla 1,06 m. V případě, že by před výskokem znížil své těžiště o 0,5 m, co je poměřně značná hodnota, jeho síla přůměrná síla odrazu by byla:

\[\frac{h}{c} + 1 = \frac{F_\mathrm{equiv}}{W}\]

\[\frac{1,06}{0.5} + 1 = \frac{F_\mathrm{equiv}}{W}\]

\[{F_\mathrm{equiv}} \approx 3 W \]

co je o 50% víc než u běžného člověka.