Výpočet svalových sil#
Výjádření vektoru síly jako přímého vlákna#
kde
\(\vec{F}\) je svalová síla o velikosti \(F\)
\(\vec{f}\) je jednotková svalová síla
kde
\(\vec{r}_p\) proximální polohový vektor, odstup svalu
\(\vec{r}_d\) distální polohový vektor, úpon svalu
Postup řešení problémů statiky#
Uvědomte si problém, zapište zadání, schematický nákres
Identifikujte těleso (bod)
Uvolněte těleso
(a) Určete vnější síly
(b) Určete vnitřní síly
Zapište rovnice rovnováhy
Ověřte řešitelnost problému
Řeště rovnice rovnováhy
Řešení problému rovnováhy v ramenním kloubu#
Zadání:#
Úloha: Člověk stojí s paží nataženou vodorovně (v rovnováze). Vypočítejte velikost síly, kterou deltový sval potřebuje k udržení natažené paže.
Hmotnost paže: 3,3 kg.
Těžiště paže: V bodě A, 24 cm od ramenního kloubu.
Síla deltového svalu: Působí v bodě B, 12 cm od ramenního kloubu pod úhlem 15° k humeru.
Úkoly:
Určte velikost síly deltového svalu (\(F_t\)).
Určte horizontální a vertikální sílu působící v ramenním kloubu.
Určte výslední sílu v ramenním kloubu a její úhel.
1. Uvědomte si problém a zapište zadání#
Těleso: Paže člověka.
Pohyb: Paže je v rovnováze, což znamená, že celkové momenty a síly jsou nulové.
Schematický nákres: Ramenní kloub je označen bodem O. Těžiště paže je bod A (24 cm od O), deltový sval působí v bodě B (12 cm od O) pod úhlem 15°.
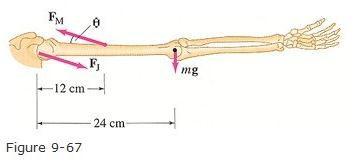
2. Identifikujte těleso (bod)#
Těleso je paže, přičemž ramenní kloub je bodem O, bod A je těžištěm paže, a bod B je místo působení síly deltového svalu.
3. Uvolněte těleso#
(a) Vnější síly:
Síla těžiště paže \(F_{g} = m g\), kde \(m = 3,3\) kg je hmotnost paže a \(g = 9,81 \, \text{m/s}^2\) je gravitační zrychlení.
(b) Vnitřní síly:
Síla deltového svalu ( F_t ), která působí pod úhlem 15° k humeru v bodě B.
Síla působící v ramenním kloubu - má horizontální a vertikální složku.
4. Zapište rovnice rovnováhy#
Pro rovnováhu musíme splnit dvě podmínky:
Rovnováha sil:
Horizontální složka:
\[ F_{\text{horizontal}} - F_t \cos(15^\circ) =0\]Vertikální složka:
\[F_{\text{vertical}} + F_t \sin(15^\circ) - F_{g} = 0\]Rovnováha momentů:
Pro rovnováhu momentů o bodě O:
\[F_t \, \sin(15^\circ)\, 12 \, \text{cm} - F_{g} \, 24 \, \text{cm} = 0\]kde:
\(F_t\) je síla deltového svalu,
\(F_g = 3,3 \, \text{kg} 9,81 \, \text{m/s}^2 = 32,4 \, \text{N}\).
5. Ověřte řešitelnost problému#
Rovnice rovnováhy momentů a sil (3 rovnice) nám umožňují spočítat sílu \(F_t\) a následně určujeme složky sil působících v ramenním kloubu (3 neznámé).
6. Řešte rovnice rovnováhy#
Výpočet síly deltového svalu#
Z rovnice rovnováhy momentů:
Výpočet horizontální a vertikální složky síly v ramenním kloubu#
Horizontální složka:
\[F_{\text{horizontal}} = 250,3 \cdot \cos(15^\circ) = 250,3 \cdot 0,9659= 241,6 \, \text{N}\]Vertikální složka:
\[F_{\text{vertical}} = - 250,3 \cdot \sin(15^\circ) + 32,4 = -250,3 \cdot 0,2588 + 32,4 = -64,8 + 32,4 = -32.4 \, \text{N} \]
Výpočet výsledné síly a jejího úhlu#
Velikost výsledné síly:
\[F_{\text{result}} = \sqrt{F_{\text{horizontal}}^2 + F_{\text{vertical}}^2} = \sqrt{241,6^2 + (-32.4,0)^2} = \sqrt{58370,6 + 1049,8} = \sqrt{59420,3} = 243,8 \, \text{N}\]Úhel výsledné síly:
\[\theta = \tan^{-1}\left( \frac{F_{\text{vertical}}}{F_{\text{horizontal}}} \right) = \tan^{-1}\left( \frac{-32,4}{241,6} \right) = \tan^{-1}(0,134) = 7,6^\circ \]
Výsledky:#
Síla deltového svalu: \(F_t = 250,3 \, \text{N}\)
Horizontální složka síly v ramenním kloubu: \(F_{\text{horizontal}} = 241,6 \, \text{N}\)
Vertikální složka síly v ramenním kloubu: \(F_{\text{vertical}} = -32,4 \, \text{N}\) - působí směrem dolu
Výsledná síla v ramenním kloubu: \(F_{\text{result}} = 243,8 \, \text{N}\)
Úhel výsledné síly: \(\theta = 7,6^\circ\)
