Pohyb ve více rozměrech#
Posuvný pohyb: V případě posuvného pohybu se pohybují všechny body tělesa stejně, t.j. po stejné trajektorii. Pro určení polohy nám tak postačí určit polohu jednoho bodu a to pomocí souřadnic nebo polohového vektoru.
Otáčivý pohyb: V lidském těle dochází především k rotačnímu pohybu v kloubech. Na rozdíl od posuvného pohybu, kde se poloha vyjadřuje pomocí souřadnic, vyjadřujeme polohu segmentu těla při rotaci pomocí úhlů rotace.
Pohyb v rovině#
Poloha bodu ve 2D Poloha bodu v rovině se nejčastěji popisuje pomocí souřadnic. Souřadnice nám umožní jednoznačně určit, kde se bod nachází vzhledem k pevně zvolenému počátku souřadnic. Poloha bodu v rovině se nejčastěji popisuje pomocí dvou souřadnic. Kartézské souřadnice jsou nejpoužívanějším způsobem, jak popsat polohu bodu v rovině. Tento systém používá dvě vzájemně kolmé osy, obvykle označované jako osa x (horizontální) a osa y (vertikální). Poloha bodu je pak určena uspořádanou dvojicí čísel (x, y), kde:
\(x\) je vzdálenost bodu od osy y měřená ve směru osy x.
\(y\) je vzdálenost bodu od osy x měřená ve směru osy y.
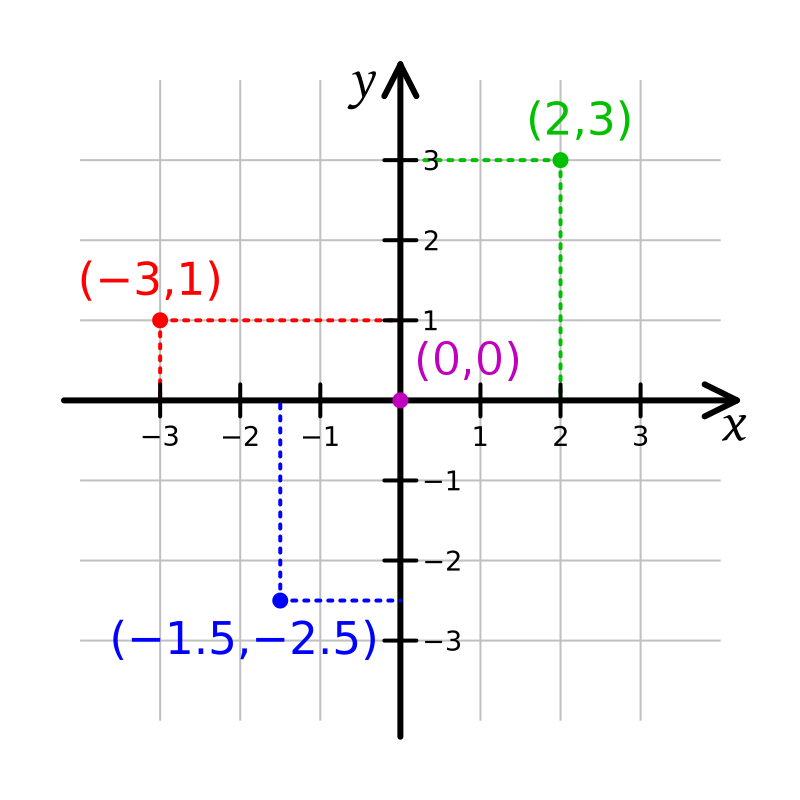
Polohový vektor je určen \(\vec{r} = (x,y)\) a jeho změnou můžeme popsat pohyb $\(\overrightarrow{\mathbf{v}}(t) = \frac{\overrightarrow{\mathbf{r}}(t_2)-\overrightarrow{\mathbf{r}}(t_1)}{t_2-t_1} = \frac{\Delta \overrightarrow{\mathbf{r}}}{\Delta t}\)$
Poloha tělesa ve 2D
Chceme-li detailně popsat polohu tělesa v rovině, můžeme kombinovat výhody kartézských pro popis polohy a úhlu natočení pro popis rotace.
Kartézské souřadnice \((x, y)\): Určují polohu tělesa vzhledem k počátku souřadného systému a osám x a y.
Úhel (\(\varphi\)): Udává úhel, který udáva natočení tělesa vůči bodu \((x,y,\) a jedné z os souřadnicového systému

Pohyb pak popíšeme jako kombinaci rotačního a translačního pohybu.
Pohyb v prostoru#
Polohu bodu v prostoru určíme pomocí tří souřadnic (\(x,y,z\)).
Polohu tělesa v prostoru určíme pomocí tří souřadnic (\(x,y,z\)) a třech natočení (\(\psi, \varphi, \vartheta, \)).
