Kinematika bodu

Kinematika

Kinematika je odvětví klasické mechaniky, které popisuje pohyb objektů bez uvážení příčin pohybu (Wikipedia).

Kinematika částice je popis pohybu, když je objekt považován za částici.

Částice jako fyzický objekt v přírodě neexistuje; je to zjednodušení pro pochopení pohybu tělesa nebo je to pojmová definice, jako je těžiště soustavy objektů.

Dráha, rychlost a zrychlení jsou tři základní veličiny popisující pohyb tělesa. Mezi nimi existují úzké vztahy, které nám umožňují popsat a analyzovat pohyb tělesa.

Dráha

• Dráha je délka trajektorie, kterou urazí těleso při svém pohybu. Je to skalární veličina a značí se obvykle písmenem s.

Rychlost

Průměrná rychlost mezi dvěma okamžiky je: $\({\mathbf{v}}(t) = \frac{s(t_2)- s(t_1)}{t_2-t_1} = \frac{\Delta s}{\Delta t}\)$

Okamžitá rychlost částice se získá, když se \(\Delta t\) přiblíží k nule.

Zrychlení

Zrychlení je změna rychlosti částice, která může být dána i rychlostí změny polohy druhého řádu.

\[{\mathbf{a}}(t) = \frac{v(t_2)-v(t_1)}{t_2-t_1} = \frac{\Delta v}{\Delta t}\]

Vztah mezi dráhou, rychlostí a zrychlením

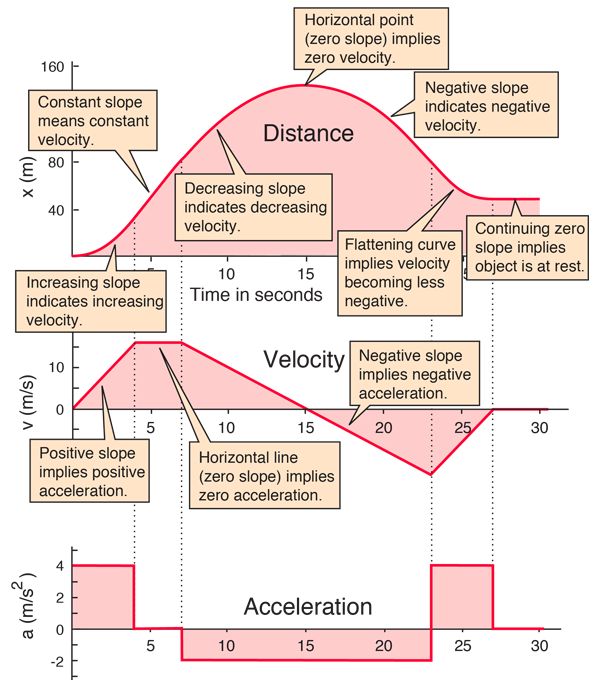
Graf dráhy: Ukazuje, jak se mění poloha tělesa v čase. Graf rychlosti: Ukazuje, jak se mění rychlost tělesa v čase. Graf zrychlení: Ukazuje, jak se mění zrychlení tělesa v čase.

Při rovnoměrném přímočarém pohybu: Rychlost je konstantní a dráha je přímo úměrná času, zrychlení je nulové. Při rovnoměrně zrychleném přímočarém pohybu: Rychlost se lineárně zvětšuje s časem a dráha se mění kvadraticky s časem.

Obecně:

• Sklon grafu dráhy určuje velikost rychlosti

• Sklon grafu rychlosti určuje velikost zrychlení

• Plocha pod grafem zrychlení je rovná změně rychlosti

• Plocha po grafem dráhy je rovna změně dráhy

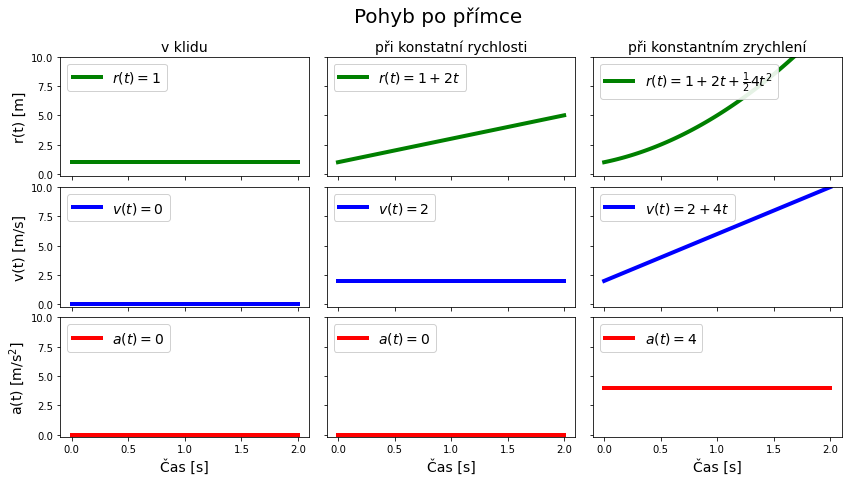
Částice při konstantní rychlosti

\begin{equation} \begin{array}{l l} \overrightarrow{\mathbf{a}}(t) = 0 \\ \overrightarrow{\mathbf{v}}(t) = \overrightarrow{\mathbf{v}}_0 \\ \overrightarrow{\mathbf{r}}(t) = \overrightarrow{\mathbf{r}}_0 + \overrightarrow{\mathbf{v}}_0t \end{array} \label{eq_constantspeed} \end{equation}

Částice při konstantním zrychlení

\begin{equation} \begin{array}{l l} \overrightarrow{\mathbf{a}}(t) = \overrightarrow{\mathbf{a}}_0 \\ \overrightarrow{\mathbf{v}}(t) = \overrightarrow{\mathbf{v}}_0 + \overrightarrow{\mathbf{a}}_0t \\ \overrightarrow{\mathbf{r}}(t) = \overrightarrow{\mathbf{r}}_0 + \overrightarrow{\mathbf{v}}_0t + \frac{1}{2}\overrightarrow{\mathbf{a}}_0 t^2 \end{array} \label{eq_constantacceleration} \end{equation}

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t = np.linspace(0, 2, 101)
r0 = 1
v0 = 2
a0 = 4

plt.rc('axes',  labelsize=14,  titlesize=14) 
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10) 
f, axarr = plt.subplots(3, 3, sharex = True, sharey = True, figsize=(14,7))
plt.suptitle('Pohyb po přímce', fontsize=20);

tones = np.ones(np.size(t))

axarr[0, 0].set_title('v klidu', fontsize=14);
axarr[0, 0].plot(t, r0*tones, 'g', linewidth=4, label='$r(t)=1$')
axarr[1, 0].plot(t,  0*tones, 'b', linewidth=4, label='$v(t)=0$')
axarr[2, 0].plot(t,  0*tones, 'r', linewidth=4, label='$a(t)=0$')
axarr[0, 0].set_ylabel('r(t) [m]')
axarr[1, 0].set_ylabel('v(t) [m/s]')
axarr[2, 0].set_ylabel('a(t) [m/s$^2$]')

axarr[0, 1].set_title('při konstatní rychlosti');
axarr[0, 1].plot(t, r0*tones+v0*t, 'g', linewidth=4, label='$r(t)=1+2t$')
axarr[1, 1].plot(t, v0*tones,      'b', linewidth=4, label='$v(t)=2$')
axarr[2, 1].plot(t,  0*tones,      'r', linewidth=4, label='$a(t)=0$')

axarr[0, 2].set_title('při konstantním zrychlení');
axarr[0, 2].plot(t, r0*tones+v0*t+1/2.*a0*t**2,'g', linewidth=4,
                 label='$r(t)=1+2t+\\frac{1}{2}4t^2$')
axarr[1, 2].plot(t, v0*tones+a0*t,             'b', linewidth=4,
                 label='$v(t)=2+4t$')
axarr[2, 2].plot(t, a0*tones,                  'r', linewidth=4,
                 label='$a(t)=4$')

for i in range(3): 
    axarr[2, i].set_xlabel('Čas [s]');
    for j in range(3):
        axarr[i,j].set_ylim((-.2, 10))
        axarr[i,j].legend(loc = 'upper left', frameon=True, framealpha = 0.9, fontsize=14)
        
plt.subplots_adjust(hspace=0.09, wspace=0.07)

Kinematika závodu na 100 m

Příkladem, kde lze analýzu některých aspektů pohybu lidského těla zredukovat na analýzu částice, je studium biomechaniky běhu na 100 metrů.

Technickou zprávu s kinematickými daty pro světový rekord na 100 m od Usaina Bolta si můžete stáhnout z website for Research Projects od Mezinárodní asociace atletických federací. Tady je přímý odkaz. Konkrétně následující tabulka ukazuje údaje pro tři medailisty v tomto závodě:

Obrázek. Údaje od tří medailistů z běhu na 100 m v Berlíně, 2009 (0print report).

Sloupec RT v tabulce výše se týká reakční doby každého sportovce. IAAF má velmi přísné pravidlo o reakční době: každý sportovec s reakční dobou kratší než 100 ms je ze soutěže diskvalifikován! Diskuzi o tomto pravidle naleznete na webu Reaction Times and Sprint False Starts.

Svou vlastní reakční dobu si můžete změřit jednoduchým způsobem na této webové stránce: http://www.humanbenchmark.com/tests/reactiontime.

Článek A Kinematics Analysis Of Three Best 100 M Performances Ever od Krzysztofa a Mera představuje podrobnou kinematickou analýzu závodů na 100 m.