Zákon zachování při periodickém pohybu

Zákon zachování při periodickém pohybu#

Kyvadlo#

Uvažujme těleso o hmotnosti $m$ zavěšené ze stropu na nehmotném vlákně o délce 1,0 m, jak ukazuje Obrázek 8.7. Částice je uvolněna z klidu, když úhel mezi vláknem a svislým směrem dolů je $30°$. Jaká je její rychlost, když dosáhne nejnižšího bodu své dráhy?

https://openstax.org/apps/archive/20250226.165223/resources/65ed9be40be5ff9da459a7a1163e71471f30ce1c

Podle naší strategie řešení problémů je prvním krokem definovat, že nás zajímá soustava částice-Země. Za druhé, na částici působí pouze gravitační síla. V problému zanedbáváme odpor vzduchu a napětí ve vlákně nevykonává žádnou práci, protože je kolmé k oblouku pohybu. Proto je mechanická energie soustavy zachována.

Protože částice začíná z klidu, nárůst kinetické energie je roven kinetické energii v nejnižším bodě. Tento nárůst kinetické energie se rovná poklesu gravitační potenciální energie, kterou můžeme vypočítat z geometrie.

můžeme napsat rovnici zachování energie vztahující se k částici v nejvyšším bodě (počáteční stav) a v nejnižším bodě kyvu (konečný stav) jako:

\[E_{k1} + E_{p1} = E_{k2} + E_{p2}\]

Protože je částice uvolněna z klidu, počáteční kinetická energie je nulová ($E_{k1} = 0$). V nejnižším bodě definujeme gravitační potenciální energii jako nulovou ($E_{p2} = 0$). Proto se naše rovnice zachování energie zjednoduší na:

\[0 + mgh = \frac{1}{2}mv^2 + 0\]

\[v = \sqrt{2gh}\]

Svislá výška částice $h$ není v zadání uvedena přímo. Můžeme ji vypočítat pomocí trigonometrie a dvou daných hodnot: délky kyvadla $L$ a úhlu $\theta$, o který je částice svisle zvednuta. Při pohledu na obrázek je svislá čárkovaná čára délka vlákna kyvadla. Svislá výška je označena jako $h$. Druhá část svislé délky vlákna lze vypočítat pomocí trigonometrie:

\[\cos\theta = \frac{x}{L} \implies x = L\cos\theta\]

Proto, při pohledu na obě části vlákna, můžeme vypočítat výšku $h$:

\[x + h = L\]

\[L\cos\theta + h = L\]

\[h = L - L\cos\theta = L(1 - \cos\theta)\]

Nyní dosadíme tuto výšku do předchozího výrazu pro rychlost, abychom získali náš výsledek:

\[v = \sqrt{2gL(1 - \cos\theta)} = \sqrt{2 \times (9.8 \, \text{m/s}^2) \times (1 \, \text{m}) \times (1 - \cos 30°)}\]

\[v = \sqrt{2 \times 9.8 \times 1 \times (1 - 0.866)} = \sqrt{19.6 \times 0.134} = \sqrt{2.6264} \approx 1.62 \, \text{m/s}\]

https://openstax.org/apps/archive/20250226.165223/resources/11ab3d97a817039dfab24454b370c606d81862bc

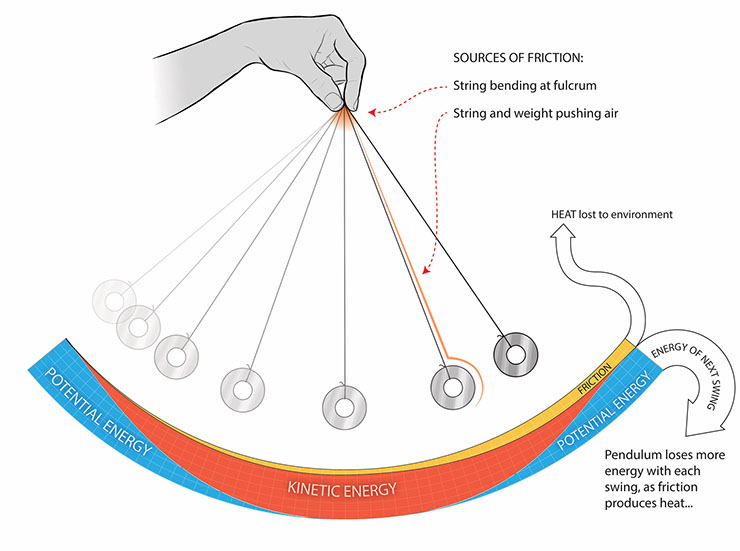
Sloupcové grafy znázorňující celkovou energii ($E$), potenciální energii ($U$) a kinetickou energii ($K$) částice v různých polohách.

(a) Celková energie soustavy se rovná potenciální energii a kinetická energie je nulová, což je v nejvyšším bodě, kterého částice dosáhne.
(b) Částice je uprostřed mezi nejvyšším a nejnižším bodem, takže sloupcové grafy kinetické a potenciální energie se rovnají celkové energii.
(c) Částice je v nejnižším bodě kyvu, takže sloupcový graf kinetické energie je nejvyšší a rovná se celkové energii soustavy.

Zákon zachování mechanické energie pro kyvadlo popisuje přeměnu mezi jeho kinetickou energií (energie pohybu) a potenciální energií (energie daná jeho polohou v gravitačním poli), za předpokladu, že na kyvadlo nepůsobí nekonzervativní síly, jako je odpor vzduchu nebo tření v závěsu.

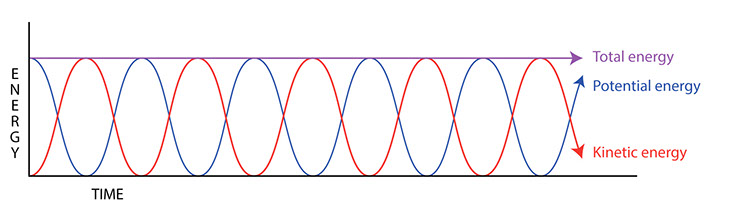
https://serpmedia.org/scigen/images/pendulum%20graph_ideal.jpg?crc=4059078340

Popis změn energie během kyvu:#

Nejvyšší bod výchylky (maximální potenciální energie, nulová kinetická energie): Když je kyvadlo vychýleno do nejvyššího bodu své dráhy a na okamžik se zastaví, má maximální potenciální gravitační energii ($E_p \= mgh$). V tomto okamžiku je jeho kinetická energie ($E_k = \frac{1}{2}mv^2$) nulová, protože jeho rychlost ($v$) je nulová.
Pohyb směrem dolů (přeměna potenciální energie na kinetickou energii): Jakmile se kyvadlo začne pohybovat směrem dolů, jeho výška $h$ klesá, a tím se zmenšuje jeho potenciální energie. Tato ztráta potenciální energie se přeměňuje na kinetickou energii, takže jeho rychlost $v$ a tím i kinetická energie ($E_k$) roste. Celková mechanická energie soustavy zůstává konstantní (za ideálních podmínek).
Nejnižší bod dráhy (minimální potenciální energie, maximální kinetická energie): V nejnižším bodě své dráhy má kyvadlo minimální potenciální energii (za předpokladu, že zde definujeme nulovou výšku, $h=0$, takže $E_p = 0$. V tomto bodě dosahuje kyvadlo své maximální rychlosti a má tedy maximální kinetickou energii ($E_k = \frac{1}{2}mv_{max}^2). Celková mechanická energie je nyní rovna kinetické energii.
Pohyb směrem nahoru (přeměna kinetické energie na potenciální energii): Když se kyvadlo pohybuje směrem nahoru na druhou stranu svého kyvu, jeho rychlost $v$ klesá, a tím se zmenšuje jeho kinetická energie. Tato ztráta kinetické energie se přeměňuje zpět na potenciální energii, takže jeho výška $h$ a potenciální energie ($E_p$) rostou. Celková mechanická energie opět zůstává konstantní.
Druhý nejvyšší bod výchylky (opět maximální potenciální energie, nulová kinetická energie): V nejvyšším bodě na druhé straně kyvu se situace opakuje jako v prvním bodě. Kinetická energie je nulová a potenciální energie je opět maximální (za ideálních podmínek dosáhne stejné výšky jako na počátku).

V ideálním kyvadle, kde nedochází ke ztrátám energie v důsledku odporu vzduchu nebo tření, je součet kinetické a potenciální energie kyvadla v libovolném bodě jeho dráhy konstantní. Energie se neustále přeměňuje mezi kinetickou a potenciální formou, ale celkové množství mechanické energie zůstává zachováno.

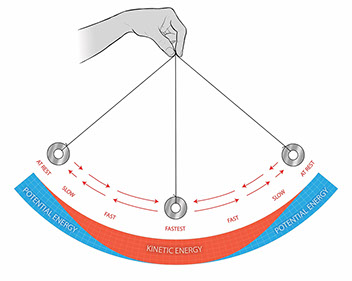
https://serpmedia.org/scigen/images/pendulum_3_ke-pe353x282.jpg?crc=4260082078

V reálném světě vždy existují nekonzervativní síly. Odpor vzduchu a tření v závěsu způsobují, že se část mechanické energie kyvadla postupně přeměňuje na teplo. To vede k postupnému snižování amplitudy kyvu a nakonec k zastavení kyvadla. V tomto případě se celková mechanická energie soustavy (kyvadlo + okolí) nezachovává, ale platí obecnější zákon zachování energie, který zahrnuje i tepelnou energii.

https://serpmedia.org/scigen/images/pendulum_4_friction.jpg?crc=494234411

Perioda matematického kyvadla#

Perioda matematického kyvadla, což je idealizovaný model sestávající z hmotného bodu zavěšeného na nehmotném a nepružném vlákně, je dána následujícím vztahem:

\[T = 2\pi \sqrt{\frac{l}{g}}\]

Kde:

$T$ značí periodu kyvadla (doba trvání jednoho úplného kmitu, tam a zpět) v sekundách (s).
$\pi$ (pí) je matematická konstanta přibližně rovná 3.14159.
$l$ je délka závěsu kyvadla v metrech (m), měřená od bodu závěsu k těžišti hmotného bodu.
$g$ je tíhové zrychlení v daném místě v metrech za sekundu na druhou (m/s²).

Z tohoto vztahu vyplývají následující důležité poznatky:

Závislost na délce: Perioda matematického kyvadla je přímo úměrná druhé odmocnině jeho délky. To znamená, že čím delší je kyvadlo, tím delší je jeho perioda (kývá se pomaleji). Pokud čtyřnásobně zvětšíme délku kyvadla, jeho perioda se zdvojnásobí.
Závislost na tíhovém zrychlení: Perioda matematického kyvadla je nepřímo úměrná druhé odmocnině tíhového zrychlení. To znamená, že čím větší je tíhové zrychlení, tím kratší je jeho perioda (kývá se rychleji). Kyvadlo bude mít například kratší periodu na planetě s vyšším tíhovým zrychlením, než na planetě s nižším tíhovým zrychlením (za stejné délky závěsu).
Nezávislost na hmotnosti: Je pozoruhodné, že perioda matematického kyvadla nezávisí na hmotnosti zavěšeného tělesa. To znamená, že kyvadla stejné délky budou mít stejnou periodu kmitání bez ohledu na to, jak těžké je jejich závaží (za předpokladu, že zanedbáme odpor vzduchu a hmotnost vlákna).
Závislost na amplitudě (pro malé výchylky): Výše uvedený vztah platí přibližně pro malé úhly výchylky (typicky do 15° od svislice). Pro větší úhly se perioda mírně prodlužuje a závisí na amplitudě kmitů. Nicméně pro malé výchylky je tato závislost zanedbatelná a pohyb kyvadla lze považovat za harmonický.

Tento vztah je fundamentální pro pochopení chování jednoduchých kyvadel a má významné aplikace v různých oblastech, včetně měření času (kyvadlové hodiny) a určování lokálního tíhového zrychlení.

Oscilátor#

Uvažujme harmonický oscilátor tvořený hmotou ($m$) připojenou k ideální pružině s tuhostí ($k$). Pokud na tento systém nepůsobí žádné nekonzervativní síly (jako je tření nebo odpor vzduchu), platí zákon zachování mechanické energie. To znamená, že celková mechanická energie oscilátoru zůstává konstantní během jeho kmitavého pohybu.

Celková mechanická energie ($E$) oscilátoru je součtem jeho kinetické energie ($E_k$) a potenciální energie pružnosti ($E_p$):

\[E = E_k + E_p = \text{konstantní}\]

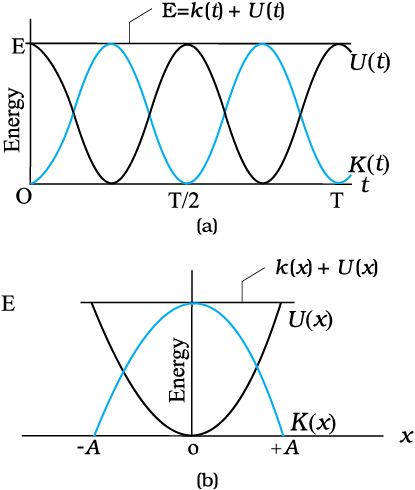
https://ncert-neetprep.s3.ap-south-1.amazonaws.com/XI/Physics/keph206/OEBPS/Images/F14.17.png

Popis změn energie během oscilací:

Maximální výchylka (amplituda, $A$): V okamžiku, kdy hmota dosáhne maximální výchylky z rovnovážné polohy (amplitudy), se na okamžik zastaví. V tomto bodě je její rychlost nulová ($v = 0$), a tedy i kinetická energie nulová ($E_k = \frac{1}{2}mv^2 = 0$). Pružina je maximálně natažená nebo stlačená, a proto je potenciální energie pružnosti maximální ($E_p = \frac{1}{2}kA^2$). Celková mechanická energie je tedy rovna maximální potenciální energii: $$E = 0 + \frac{1}{2}kA^2 = \frac{1}{2}kA^2$$
Pohyb k rovnovážné poloze: Jak se hmota začne pohybovat zpět k rovnovážné poloze, pružina koná práci a urychluje hmotu. Potenciální energie pružnosti se zmenšuje, protože se zmenšuje protažení nebo stlačení pružiny. Tato ztráta potenciální energie se přeměňuje na kinetickou energii, takže rychlost hmoty a její kinetická energie rostou. Celková mechanická energie zůstává konstantní.
Rovnovážná poloha ($x = 0$): Když hmota prochází rovnovážnou polohou, pružina není ani natažená, ani stlačená, takže její potenciální energie pružnosti je nulová ($E_p = \frac{1}{2}kx^2 = 0$). V tomto bodě má hmota maximální rychlost ($v_{max}$) a tedy maximální kinetickou energii ($E_k = \frac{1}{2}mv_{max}^2$). Celková mechanická energie je nyní rovna maximální kinetické energii: $$E = 0 + \frac{1}{2}mv_{max}^2 = \frac{1}{2}mv_{max}^2$$

Ze zákona zachování energie vyplývá, že maximální potenciální energie v amplitudě je rovna maximální kinetické energii v rovnovážné poloze: $$\frac{1}{2}kA^2 = \frac{1}{2}mv_{max}^2$$
Pohyb za rovnovážnou polohu: Hmota pokračuje v pohybu za rovnovážnou polohu, čímž začíná pružinu stlačovat (nebo dále natahovat). Pružina nyní působí proti pohybu hmoty a zpomaluje ji. Kinetická energie se přeměňuje zpět na potenciální energii pružnosti, která se zvětšuje s rostoucím stlačením nebo natažením pružiny.
Druhá maximální výchylka ($-A$): V okamžiku, kdy hmota dosáhne maximální výchylky na opačné straně rovnovážné polohy, se opět na okamžik zastaví. Její kinetická energie je opět nulová a potenciální energie pružnosti je opět maximální ($\frac{1}{2}kA^2$).

V ideálním harmonickém oscilátoru bez disipativních sil je součet kinetické energie hmoty a potenciální energie pružnosti v libovolném okamžiku konstantní. Energie se neustále přeměňuje mezi kinetickou a potenciální formou, ale celkové množství mechanické energie zůstává zachováno.

https://www.compadre.org/nexusph/course/images/Energy/EnSprPEgraph2.jpg

Reálný oscilátor:

V reálných systémech vždy existují disipativní síly, jako je tření a odpor vzduchu. Tyto síly konají zápornou práci na oscilátoru a způsobují, že se část mechanické energie přeměňuje na teplo. V důsledku toho se celková mechanická energie oscilátoru postupně snižuje a amplituda kmitů se zmenšuje až do úplného zastavení. V tomto případě platí obecnější zákon zachování energie, který zahrnuje i tepelnou energii.