Příklady zachování energie

Práce a energie sprintera

Práce vykonaná pro zrychlení sprintera a zvýšení jeho kinetické energie pochází převážně ze stahování a natahování svalových vláken a šlach, které fungují podobně jako pružiny. Práce vykonaná svalem při kontrakci je součinem síly, kterou vyvine, a vzdálenosti, o kterou se zkrátí. Velikost síly, kterou sval dokáže vyvinout při dané kontrakci, závisí na rychlosti kontrakce; čím pomalejší je kontrakce, tím větší je síla.

Film běžícího muže (hmotnost 70 kg) ukázal, že z klidu zrychlil na 3,0 m/s v prvním kroku, na 4,2 m/s ve druhém kroku (zatímco druhá noha byla na zemi) a na 5,0 m/s ve třetím kroku.

Kinetickou energii sprintera lze vypočítat pro každý krok:

Krok	Rychlost (m/s)	\(E_k\) (J)	\(\Delta E_k\) (J)
0	0	0	-
1	3.0	315	315
2	4.2	617	302
3	5.0	875	258

Každá změna kinetické energie byla způsobena prací vykonanou jeho svaly. Změna se s každým krokem mírně snižuje, protože mezi kroky je méně času, což snižuje množství práce, kterou jeho svaly mohou vykonat při stejné kontrakci. Zvýšení energie tedy nemůže trvat věčně! Práce vykonaná svaly, když se sprinter pohybuje konstantní rychlostí, slouží k vyrovnání různých ztrát energie: tření v kloubech, odpor vzduchu a ztráty tepla v šlachách při jejich natahování a smršťování.

Přibližně 2,5 % metabolické energie (měřené spotřebou kyslíku) se spotřebuje na překonání odporu vzduchu při rychlosti 6 m/s v klidném vzduchu, přibližně 13 % při sprinterské rychlosti 10 m/s. To odpovídá skutečnosti, že odpor vzduchu je funkcí rychlosti.

Jak vysoko dokážete skočit?

Předpokládejme, že chcete vyskočit co nejvýše z klidové polohy. Ohnete nohy a pak je rychle natáhnete. Podívejte se, jak se mění vaše těžiště, dokud jste ještě na zemi:

Poloha	Vzdálenost těžiště od země
1. Stoj vzpřímený	1.0 m
2. Kolena ohnutá	0.65 m
3. Konec odrazu	1.05 m

O jakou vzdálenost jste zrychlili své těžiště? (Poloha 3 - Poloha 2) 0.4 m

Studie sportovců skákajících z tenzometrických plošin ukazují, že maximální síla působící proti zemi je přibližně 2,3násobek tělesné hmotnosti \(W\) a že průměrná síla je přibližně \(2W_B\).

Práce vykonaná skokanem je rovna průměrné síle násobené dráhou zrychlení těžiště:

\[W = (2W_B-W_B) \times 0.4 \, \text{m} = 0.4W \, \text{m}\]

Změna potenciální energie je rovna hmotnosti skokana \(m\) krát tíhové zrychlení \(g\) krát výška \(\Delta h\):

\[ \begin{align}\begin{aligned}\Delta E_p = mg\Delta h = W\Delta h$$, \\kde $W = mg$ je tíha skokana.\\Z rovnosti práce a změny potenciální energie: $0.4W = W\Delta h$, z čehož vyplývá $\Delta h = 0.4 \, \text{m}$.\\Konečná výška těžiště nad zemí bude počáteční výška těžiště při konci odrazu plus změna výšky: $1.05 \, \text{m} + 0.4 \, \text{m} = 1.45 \, \text{m}$.\\## Skok o tyči\\Dobrý odhad výšky dosažené tyčkařem vychází z výpočtu zachování energie. Zde je příklad. Konečná rychlost tyčkaře (právě když je tyč zapíchnuta do země) je 9,5 m/s. Těžiště skokana je 0,9 m nad zemí. Na vrcholu skoku je těžiště 0,1 m nad laťkou. Použijte zákon zachování energie k nalezení výšky laťky nad zemí. (Světový rekord je něco málo přes 6 metrů.) \\Počáteční energie tyčkaře je součtem kinetické energie a potenciální energie:\\$$E_1 = E_{k1} + E_{p1} = \frac{1}{2}mv^2 + mg h_1\end{aligned}\end{align} \]

kde \(m\) je hmotnost, \(v\) je rychlost a \(h_1\) je počáteční výška těžiště.

Na vrcholu skoku je energie rovna potenciální energii těžiště nad laťkou plus potenciální energii laťky:

\[E_2 = E_{k2} + E_{p2} = \frac{1}{2}mv_2^2 + mg (h_{\text{bar}} + 0.1)\]

kde \(v_2\) je horizontální rychlost na vrcholu (nenulová, ale pro jednoduchost zanedbáme, pokud není uvedena) a \(h_\text{bar}\) je výška laťky.

Pokud zanedbáme ztráty energie, pak \(E_1 = E_2\):

\[\frac{1}{2}mv^2 + mg h_1 = \frac{1}{2}mv_2^2 + mg (h_{bar} + 0.1)\]

Pokud zanedbáme horizontální rychlost na vrcholu (\(v_f \approx 0\)), pak:

\[\frac{1}{2}mv^2 + mg h_i = mg (h_{bar} + 0.1)\]

Vydělíme celou rovnici hmotností \(m\):

\[\frac{1}{2}v^2 + g h_i = g (h_{bar} + 0.1)\]

Nyní můžeme dosadit hodnoty (\(v = 9.5 \, \text{m/s}\), \(h_i = 0.9 \, \text{m}\), \(g \approx 9.8 \, \text{m/s}^2\)):

\(\frac{1}{2}(9.5)^2 + 9.8(0.9) = 9.8 (h_{bar} + 0.1)\)

\(45.125 + 8.82 = 9.8 h_{bar} + 0.98\)

\(53.945 = 9.8 h_{bar} + 0.98\)

\(52.965 = 9.8 h_{bar}\)

\(h_{bar} = \frac{52.965}{9.8} \approx 5.4 \, \text{m}\)

Hmotnost sportovce není potřeba znát, protože se z rovnice vykrátí, pokud zanedbáme ztráty energie a horizontální rychlost na vrcholu skoku.

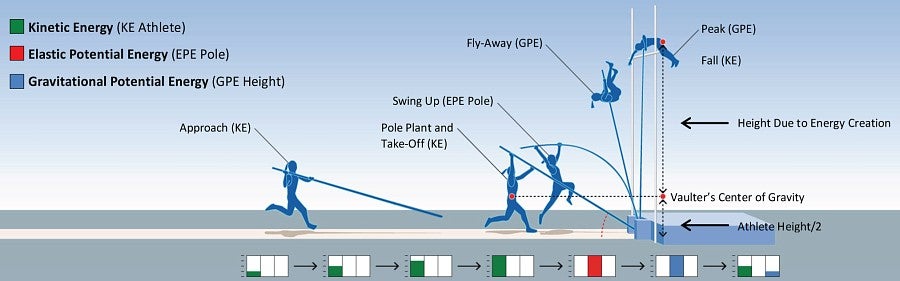
Procesy přenosu energie při skoku o tyči jsou poněkud složité, ale výše uvedený základní výpočet dává dobrý odhad konečného výsledku. Sportovec vykonává práci, táhne dolů tyč a zároveň stoupá. Velkou část práce na sportovci vykonává tyč uvolněním elastické potenciální energie. Dochází k určitým ztrátám energie – tyč se mírně zahřívá. A tyčkař má na vrcholu malou vodorovnou rychlost, a proto si zachovává část kinetické energie. Základní vztah přeměny energie však platí:

Note

Kinetická energie → Elastická potenciální energie → Gravitační potenciální energie.

Caution

Pro maximalizaci výšky skoku o tyči tyčkaři ohýbají své tělo kolem laťky (jak je znázorněno na obrázku níže). Tímto způsobem může jejich těžiště (červená tečka) ve skutečnosti projít pod laťkou, zatímco jejich tělo je schopno laťku překonat (černá tečka). To znamená, že laťka může být ve skutečnosti umístěna výše, než je maximální výška dosažená těžištěm tyčkaře.